Chapter 2 Supplementary Materials for Batch Effects Management in Case Studies
2.1 Sponge data
2.1.1 Data pre-processing
2.1.1.1 Pre-filtering
We load the sponge data stored internally with function data().
# Sponge data
data('sponge_data')
sponge.tss <- sponge_data$X.tss
dim(sponge.tss)## [1] 32 24# zero proportion
mean(sponge.tss == 0)## [1] 0.5455729The sponge data include the relative abundance of 24 OTUs and 32 samples. Given the small number of OTUs we advise not to pre-filter the data.
2.1.1.2 Transformation
Prior to CLR transformation, we recommend adding 0.01 as the offset for the sponge data - that are relative abundance data. We use logratio.transfo() function in mixOmics package to CLR transform the data.
sponge.clr <- logratio.transfo(X = sponge.tss, logratio = 'CLR', offset = 0.01)
class(sponge.clr) <- 'matrix'2.1.2 Batch effect detection
2.1.2.1 PCA
We apply pca() function from mixOmics package to the sponge data and Scatter_Density() function from PLSDAbatch to represent the PCA sample plot with densities.
sponge.pca.before <- pca(sponge.clr, ncomp = 3, scale = TRUE)
sponge.batch <- sponge_data$Y.bat
sponge.trt <- sponge_data$Y.trt
Scatter_Density(object = sponge.pca.before,
batch = sponge.batch,
trt = sponge.trt, title = 'Sponge data',
trt.legend.title = 'Tissue types')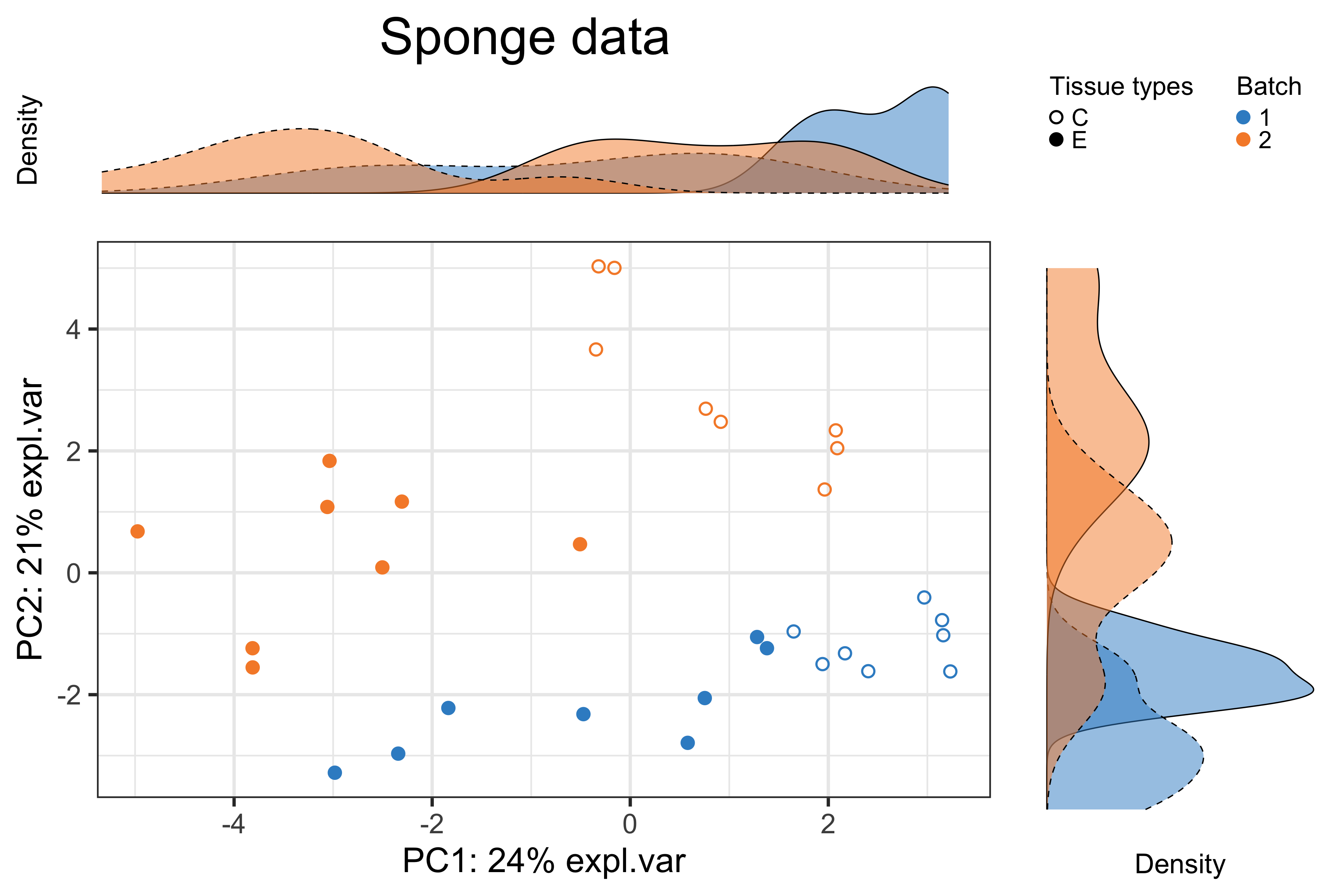
Figure 2.1: The PCA sample plot with densities in the sponge data.
In the above figure, the tissue variation (effects of interest) accounted for 24% of data variance on component 1, while the gel variation (batch effects) for 21% on component 2. Therefore, the batch effect is slightly weaker than the treatment effect in the sponge data.
2.1.2.2 Heatmap
We produce a heatmap using pheatmap package. The data first need to be scaled on both OTUs and samples.
# scale the clr data on both OTUs and samples
sponge.clr.s <- scale(sponge.clr, center = T, scale = T)
sponge.clr.ss <- scale(t(sponge.clr.s), center = T, scale = T)
sponge.anno_col <- data.frame(Batch = sponge.batch, Tissue = sponge.trt)
sponge.anno_colors <- list(Batch = color.mixo(1:2),
Tissue = pb_color(1:2))
names(sponge.anno_colors$Batch) = levels(sponge.batch)
names(sponge.anno_colors$Tissue) = levels(sponge.trt)
pheatmap(sponge.clr.ss,
cluster_rows = F,
fontsize_row = 4,
fontsize_col = 6,
fontsize = 8,
clustering_distance_rows = 'euclidean',
clustering_method = 'ward.D',
treeheight_row = 30,
annotation_col = sponge.anno_col,
annotation_colors = sponge.anno_colors,
border_color = 'NA',
main = 'Sponge data - Scaled')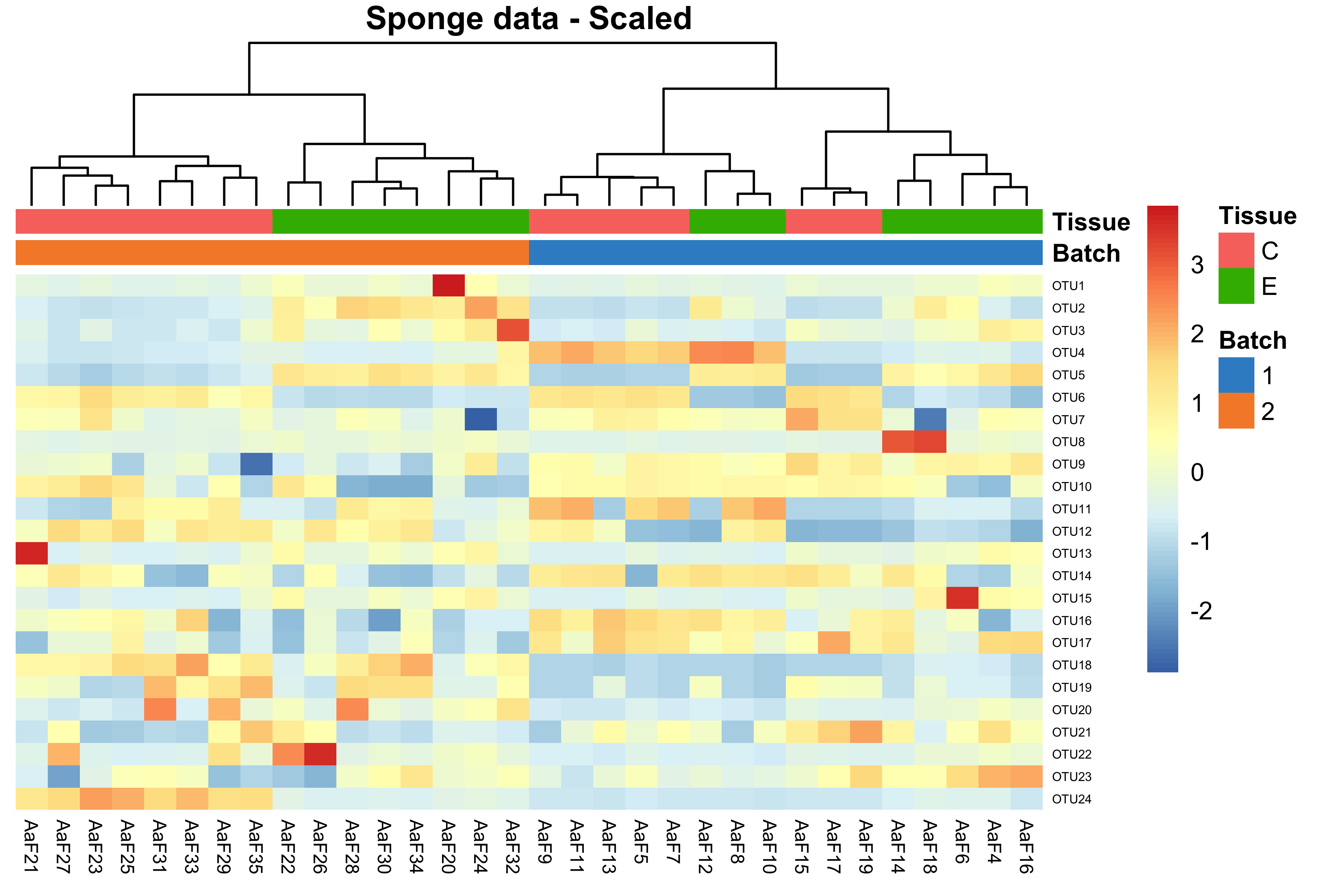
Figure 2.2: Hierarchical clustering for samples in the sponge data.
In the heatmap, samples in the sponge data were clustered or grouped by batches instead of tissues, indicating a batch effect.
2.1.2.3 pRDA
We apply pRDA with varpart() function from vegan R package.
sponge.factors.df <- data.frame(trt = sponge.trt,
batch = sponge.batch)
sponge.rda.before <- varpart(sponge.clr, ~ trt, ~ batch,
data = sponge.factors.df,
scale = T)
sponge.rda.before$part$indfract## Df R.squared Adj.R.squared Testable
## [a] = X1|X2 1 NA 0.16572246 TRUE
## [b] = X2|X1 1 NA 0.16396277 TRUE
## [c] 0 NA -0.01063501 FALSE
## [d] = Residuals NA NA 0.68094977 FALSEIn the result, X1 and X2 represent the first and second covariates fitted in the model. [a], [b] represent the independent proportion of variance explained by X1 and X2 respectively, and [c] represents the intersection variance shared between X1 and X2. The sponge data have a completely balanced batch x treatment design, so there was no intersection variance (indicated in line [c], Adj.R.squared = -0.01) detected. The proportion of treatment and batch variance was nearly equal as indicated in lines [a] and [b].
2.1.3 Managing batch effects
2.1.3.1 Accounting for batch effects
The methods that we use to account for batch effects include the method designed for microbiome data: zero-inflated Gaussian (ZIG) mixture model and the methods adapted for microbiome data: linear regression, SVA and RUV4. Among them, SVA and RUV4 are designed for unknown batch effects.
As the ZIG model is applicable to counts data, the sponge data are not qualified for this model. We therefore only apply the methods that can be adapted for microbiome data.
Linear regression
Linear regression is conducted with linear_regres() function in PLSDAbatch. We integrated the performance package that assesses performance of regression models into our function linear_regres(). Therefore, we can apply check_model() from performance to the outputs from linear_regres() to diagnose the validity of the model fitted with treatment and batch effects for each variable (LÃŒdecke et al. 2020). We can extract performance measurements such as adjusted R2, RMSE, RSE, AIC and BIC for the models fitted with and without batch effects, which are also the outputs of linear_regres().
We apply type = "linear model" to the sponge data because of the balanced batch x treatment design.
sponge.clr <- sponge.clr[1:nrow(sponge.clr), 1:ncol(sponge.clr)]
sponge.lm <- linear_regres(data = sponge.clr,
trt = sponge.trt,
batch.fix = sponge.batch,
type = 'linear model')
sponge.p <- sapply(sponge.lm$lm.table, function(x){x$coefficients[2,4]})
sponge.p.adj <- p.adjust(p = sponge.p, method = 'fdr')
check_model(sponge.lm$model$OTU2)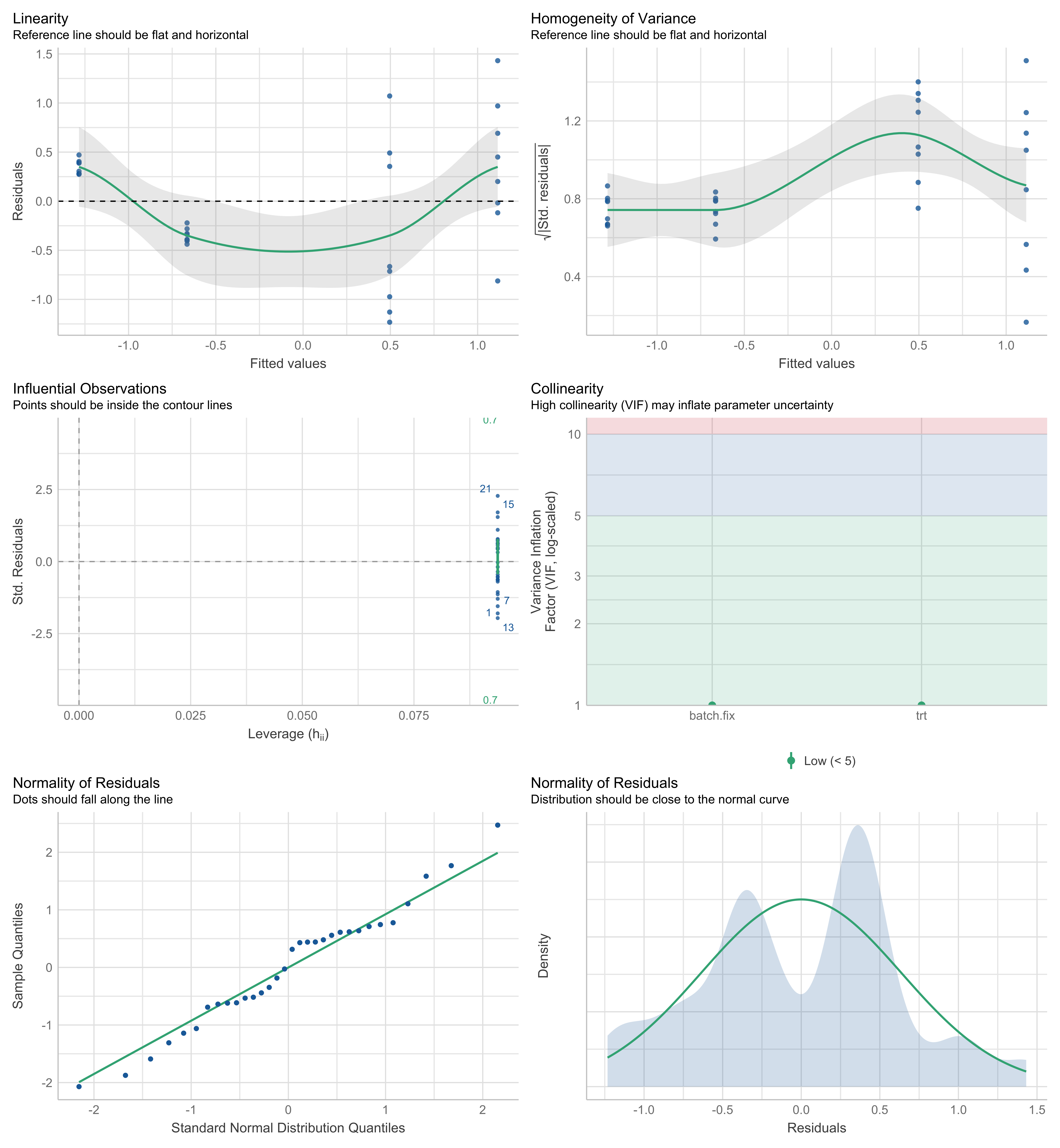
Figure 2.3: Diagnostic plots for the model fitted with batch effects of “OTU2” in the sponge data.
To diagnose the validity of the model fitted with both treatment and batch effects, we use different plots to check the assumptions of each microbial variable. For example, the diagnostic plots of “OTU2” are shown in the above figure panel. The simulated data under the fitted model were not very close to the real data (shown as green line), indicating an imperfect fitness (top panel). The linearity (or homoscedasticity) and homogeneity of variance were not satisfied. The correlation between batch (batch.fix) and treatment (trt) effects was very low, indicating a good model with low collinearity. Some samples could be classified as outliers with a Cook’s distance larger than or equal to 0.5, for example, “21”, “15”, “7”, “1” and “13” (middle panel). The distribution of residuals was not close to normal (bottom panel). For the microbial variables with some assumptions not met, we should be careful about their results.
For performance measurements of models fitted with or without batch effects, we show an example of the results for some variables.
head(sponge.lm$adj.R2)## trt.only trt.batch
## OTU1 0.06423228 0.05701977
## OTU2 0.60492094 0.67117014
## OTU3 0.19003076 0.18125188
## OTU4 -0.03327738 0.23731780
## OTU5 0.97483298 0.97643741
## OTU6 0.97496003 0.97634939If the adjusted \(R^2\) of the model with both treatment and batch effects is larger than the model with treatment effects only, e.g., OTU2, OTU4, OTU5 and OTU6, the model fitted with batch effects explains more data variance, and is thus better than the model without batch effects. Otherwise, the batch effect is not necessary to be added into the linear model.
We next look at the AIC of models fitted with or without batch effects.
head(sponge.lm$AIC)## trt.only trt.batch
## OTU1 47.901506 49.0623531
## OTU2 74.001621 69.0433180
## OTU3 -5.630456 -4.3703385
## OTU4 90.699895 81.8982606
## OTU5 21.727333 20.5345128
## OTU6 1.196912 0.2853681A lower AIC indicates a better fit. Both results of the adjusted \(R^2\) and AIC were consistent on model selection for the listed OTUs.
SVA
SVA accounts for unknown batch effects. Here we assume that the batch grouping information in the sponge data is unknown. We first build two design matrices with (sponge.mod) and without (sponge.mod0) treatment grouping information generated with model.matrix() function from stats. We then use num.sv() from sva package to determine the number of batch variables n.sv that is used to estimate batch effects in function sva().
# estimate batch matrix
sponge.mod <- model.matrix( ~ sponge.trt)
sponge.mod0 <- model.matrix( ~ 1, data = sponge.trt)
sponge.sva.n <- num.sv(dat = t(sponge.clr), mod = sponge.mod, method = 'leek')
sponge.sva <- sva(t(sponge.clr), sponge.mod, sponge.mod0, n.sv = sponge.sva.n)## Number of significant surrogate variables is: 1
## Iteration (out of 5 ):1 2 3 4 5The estimated batch effects are then applied to f.pvalue() to calculate the P-values of treatment effects. The estimated batch effects in SVA are assumed to be independent of the treatment effects. However, SVA considers some correlation between batch and treatment effects (Y. Wang and LêCao 2020).
# include estimated batch effects in the linear model
sponge.mod.batch <- cbind(sponge.mod, sponge.sva$sv)
sponge.mod0.batch <- cbind(sponge.mod0, sponge.sva$sv)
sponge.sva.p <- f.pvalue(t(sponge.clr), sponge.mod.batch, sponge.mod0.batch)
sponge.sva.p.adj <- p.adjust(sponge.sva.p, method = 'fdr')RUV4
Before applying RUV4 (RUV4() from ruv package), we need to specify negative control variables and the number of batch variables to estimate. We can use the empirical negative controls that are not significantly differentially abundant (adjusted P > 0.05) from a linear regression with the treatment information as the only covariate.
We use a loop to fit a linear regression for each microbial variable and adjust P values of treatment effects for multiple comparisons with p.adjust() from stats. The empirical negative controls are then extracted according to the adjusted P values.
# empirical negative controls
sponge.empir.p <- c()
for(e in 1:ncol(sponge.clr)){
sponge.empir.lm <- lm(sponge.clr[,e] ~ sponge.trt)
sponge.empir.p[e] <- summary(sponge.empir.lm)$coefficients[2,4]
}
sponge.empir.p.adj <- p.adjust(p = sponge.empir.p, method = 'fdr')
sponge.nc <- sponge.empir.p.adj > 0.05The number of batch variables k can be determined using getK() function.
# estimate k
sponge.k.res <- getK(Y = sponge.clr, X = sponge.trt, ctl = sponge.nc)
sponge.k <- sponge.k.res$k
sponge.k <- ifelse(sponge.k != 0, sponge.k, 1)We then apply RUV4() with known treatment variables, estimated negative control variables and k batch variables. The calculated P values also need to be adjusted for multiple comparisons.
sponge.ruv4 <- RUV4(Y = sponge.clr, X = sponge.trt,
ctl = sponge.nc, k = sponge.k)
sponge.ruv4.p <- sponge.ruv4$p
sponge.ruv4.p.adj <- p.adjust(sponge.ruv4.p, method = "fdr")Note: A package named RUVSeq has been developed for count data. It provides RUVg() using negative control variables, and also other functions RUVs() and RUVr() using sample replicates (Moskovicz et al. 2020) or residuals from the regression on treatment effects to estimate and then account for latent batch effects. However, for CLR-transformed data, we still recommend the standard ruv package.
2.1.3.2 Correcting for batch effects
The methods that we use to correct for batch effects include removeBatchEffect, ComBat, PLSDA-batch, sPLSDA-batch, Percentile Normalisation and RUVIII. Among them, RUVIII is designed for unknown batch effects. Except RUVIII that requires sample replicates which the sponge data do not have, these methods were all applied to and illustrated with the sponge data.
removeBatchEffect
The removeBatchEffect() function is implemented in limma package. The design matrix (design) with treatment grouping information can be generated with model.matrix() function from stats as shown in section accounting for batch effects method “SVA”.
Here we use removeBatchEffect() function with batch grouping information (batch) and treatment design matrix (design) to calculate batch effect corrected data sponge.rBE.
sponge.rBE <- t(removeBatchEffect(t(sponge.clr), batch = sponge.batch,
design = sponge.mod))ComBat
The ComBat() function (from sva package) is implemented as parametric or non-parametric correction with option par.prior. Under a parametric adjustment, we can assess the model’s validity with prior.plots = T (Leek et al. 2012).
Here we use a non-parametric correction (par.prior = FALSE) with batch grouping information (batch) and treatment design matrix (mod) to calculate batch effect corrected data sponge.ComBat.
sponge.ComBat <- t(ComBat(t(sponge.clr), batch = sponge.batch,
mod = sponge.mod, par.prior = F))PLSDA-batch
The PLSDA_batch() function is implemented in PLSDAbatch package. To use this function, we need to specify the optimal number of components related to treatment (ncomp.trt) or batch effects (ncomp.bat).
Here in the sponge data, we use plsda() from mixOmics with only treatment grouping information to estimate the optimal number of treatment components to preserve.
# estimate the number of treatment components
sponge.trt.tune <- plsda(X = sponge.clr, Y = sponge.trt, ncomp = 5)
sponge.trt.tune$prop_expl_var #1## $X
## comp1 comp2 comp3 comp4 comp5
## 0.22802218 0.10478658 0.16376238 0.06861581 0.04524292
##
## $Y
## comp1 comp2 comp3 comp4 comp5
## 1.00000000 0.16584332 0.06024061 0.03278432 0.01144732We choose the number that explains 100% variance in the outcome matrix Y, thus from the result, 1 component was enough to preserve the treatment information.
We then use PLSDA_batch() function with both treatment and batch grouping information to estimate the optimal number of batch components to remove.
# estimate the number of batch components
sponge.batch.tune <- PLSDA_batch(X = sponge.clr,
Y.trt = sponge.trt,
Y.bat = sponge.batch,
ncomp.trt = 1,
ncomp.bat = 5)
sponge.batch.tune$explained_variance.bat #1## $X
## comp1 comp2 comp3 comp4 comp5
## 0.27660372 0.08286158 0.08187289 0.07026693 0.07081271
##
## $Y
## comp1 comp2 comp3 comp4 comp5
## 1 1 1 1 1Using the same criterion as choosing treatment components, we choose the number of batch components that explains 100% variance in the outcome matrix of batch. According to the result, 1 component was required to remove batch effects.
We then can correct for batch effects applying PLSDA_batch() with treatment, batch grouping information and corresponding optimal number of related components.
sponge.PLSDA_batch.res <- PLSDA_batch(X = sponge.clr,
Y.trt = sponge.trt,
Y.bat = sponge.batch,
ncomp.trt = 1,
ncomp.bat = 1)
sponge.PLSDA_batch <- sponge.PLSDA_batch.res$X.nobatchsPLSDA-batch
We apply sPLSDA-batch using the same function PLSDA_batch() but we specify the number of variables to select on each component (usually only treatment-related components keepX.trt). To determine the optimal number of variables to select, we use tune.splsda() function from mixOmics package (Rohart et al. 2017) with all possible numbers of variables to select for each component (test.keepX).
# estimate the number of variables to select per treatment component
set.seed(777)
sponge.test.keepX = seq(1, 24, 1)
sponge.trt.tune.v <- tune.splsda(X = sponge.clr,
Y = sponge.trt,
ncomp = 1,
test.keepX = sponge.test.keepX,
validation = 'Mfold',
folds = 4, nrepeat = 50)
sponge.trt.tune.v$choice.keepX #1## comp1
## 1Here the optimal number of variables to select for the treatment component was 1. Since we have adjusted the amount of treatment variation to preserve, we need to re-choose the optimal number of components related to batch effects using the same criterion mentioned in section correcting for batch effects method “PLSDA-batch”.
# estimate the number of batch components
sponge.batch.tune <- PLSDA_batch(X = sponge.clr,
Y.trt = sponge.trt,
Y.bat = sponge.batch,
ncomp.trt = 1,
keepX.trt = 1,
ncomp.bat = 5)
sponge.batch.tune$explained_variance.bat #1## $X
## comp1 comp2 comp3 comp4 comp5
## 0.25672979 0.07716171 0.08936628 0.08434746 0.09422519
##
## $Y
## comp1 comp2 comp3 comp4 comp5
## 1 1 1 1 1According to the result, we needed only 1 batch related component to remove batch variance from the data with function PLSDA_batch().
sponge.sPLSDA_batch.res <- PLSDA_batch(X = sponge.clr,
Y.trt = sponge.trt,
Y.bat = sponge.batch,
ncomp.trt = 1,
keepX.trt = 1,
ncomp.bat = 1)
sponge.sPLSDA_batch <- sponge.sPLSDA_batch.res$X.nobatchNote: for unbalanced batch x treatment design (with the exception of the nested design), we can specify balance = FALSE in PLSDA_batch() function to apply weighted PLSDA-batch.
Percentile Normalisation
To apply percentile_norm() function from PLSDAbatch package, we need to indicate a control group (ctrl.grp).
sponge.PN <- percentile_norm(data = sponge.clr,
batch = sponge.batch,
trt = sponge.trt,
ctrl.grp = 'C')2.1.4 Assessing batch effect correction
We apply different visualisation and quantitative methods to assessing batch effect correction.
2.1.4.1 Methods that detect batch effects
PCA
In the sponge data, we compared the PCA sample plots before and after batch effect correction with different methods.
sponge.pca.before <- pca(sponge.clr, ncomp = 3,
scale = TRUE)
sponge.pca.rBE <- pca(sponge.rBE, ncomp = 3,
scale = TRUE)
sponge.pca.ComBat <- pca(sponge.ComBat, ncomp = 3,
scale = TRUE)
sponge.pca.PLSDA_batch <- pca(sponge.PLSDA_batch, ncomp = 3,
scale = TRUE)
sponge.pca.sPLSDA_batch <- pca(sponge.sPLSDA_batch, ncomp = 3,
scale = TRUE)
sponge.pca.PN <- pca(sponge.PN, ncomp = 3,
scale = TRUE)sponge.pca.before.plot <-
Scatter_Density(object = sponge.pca.before,
batch = sponge.batch,
trt = sponge.trt,
title = 'Before',
trt.legend.title = 'Tissue')sponge.pca.rBE.plot <-
Scatter_Density(object = sponge.pca.rBE,
batch = sponge.batch,
trt = sponge.trt,
title = 'removeBatchEffect',
trt.legend.title = 'Tissue')sponge.pca.ComBat.plot <-
Scatter_Density(object = sponge.pca.ComBat,
batch = sponge.batch,
trt = sponge.trt,
title = 'ComBat',
trt.legend.title = 'Tissue')sponge.pca.PLSDA_batch.plot <-
Scatter_Density(object = sponge.pca.PLSDA_batch,
batch = sponge.batch,
trt = sponge.trt,
title = 'PLSDA-batch',
trt.legend.title = 'Tissue')sponge.pca.sPLSDA_batch.plot <-
Scatter_Density(object = sponge.pca.sPLSDA_batch,
batch = sponge.batch,
trt = sponge.trt,
title = 'sPLSDA-batch',
trt.legend.title = 'Tissue')sponge.pca.PN.plot <-
Scatter_Density(object = sponge.pca.PN,
batch = sponge.batch,
trt = sponge.trt,
title = 'Percentile Normalisation',
trt.legend.title = 'Tissue')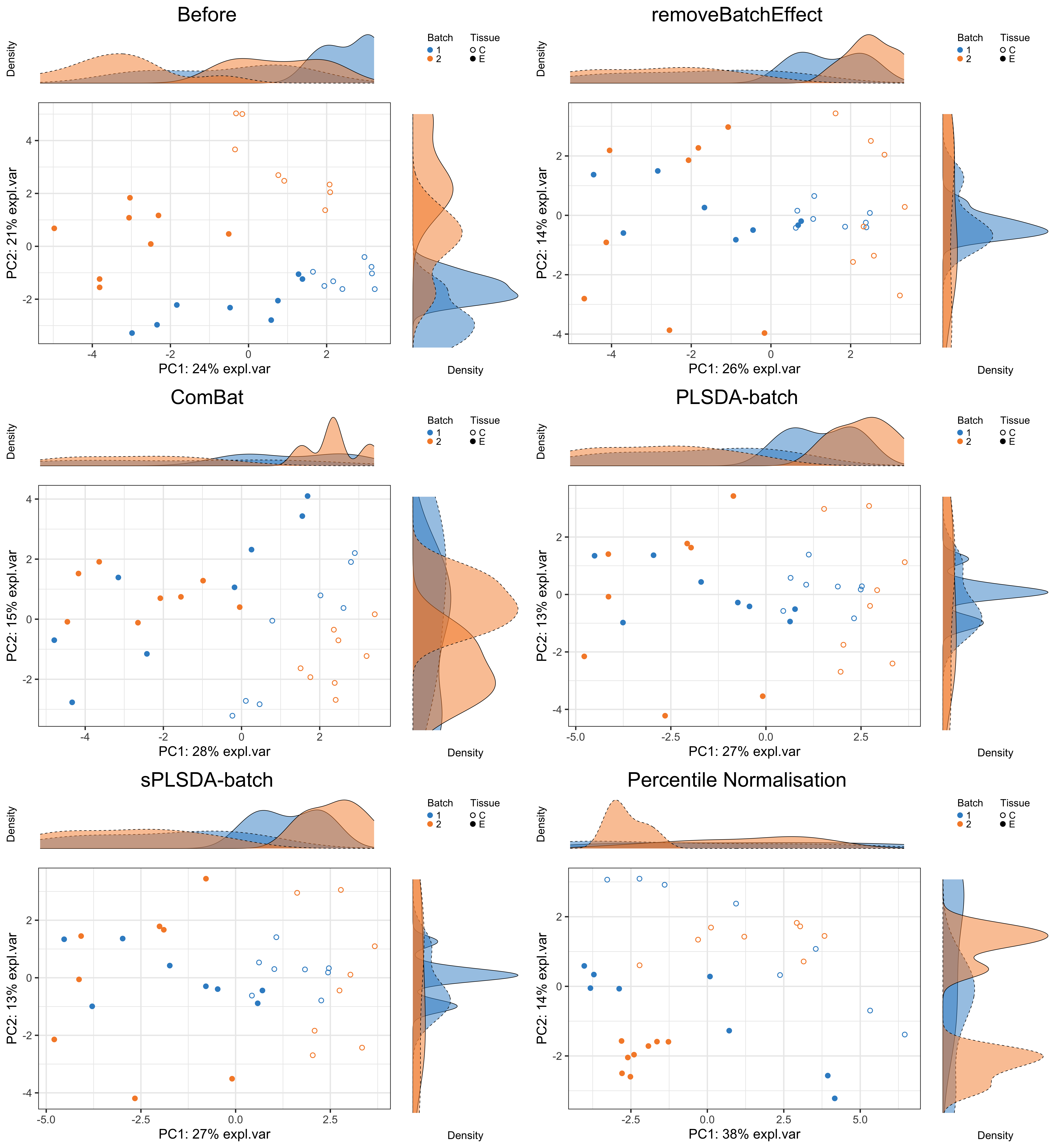
Figure 2.4: The PCA sample plots with densities before and after batch effect correction in the sponge data.
As shown in the PCA sample plots, the difference between the samples from two different batches was removed after batch effect correction with most methods except percentile normalisation. In the data corrected with percentile normalisation, the samples from tissue E still included a distinction between samples from two batches. We can also compare the boxplots and density plots for key variables identified in PCA driving the major variance or heatmaps showing obvious patterns before and after batch effect correction (results not shown).
pRDA
We calculate the global explained variance across all microbial variables using pRDA. To achieve this, we create a loop for each variable from the original (uncorrected) and batch effect-corrected data. The final results are then displayed with partVar_plot() from PLSDAbatch package.
sponge.corrected.list <- list(`Before correction` = sponge.clr,
removeBatchEffect = sponge.rBE,
ComBat = sponge.ComBat,
`PLSDA-batch` = sponge.PLSDA_batch,
`sPLSDA-batch` = sponge.sPLSDA_batch,
`Percentile Normalisation` = sponge.PN)
sponge.prop.df <- data.frame(Treatment = NA, Batch = NA,
Intersection = NA,
Residuals = NA)
for(i in 1:length(sponge.corrected.list)){
rda.res = varpart(sponge.corrected.list[[i]], ~ trt, ~ batch,
data = sponge.factors.df, scale = T)
sponge.prop.df[i, ] <- rda.res$part$indfract$Adj.R.squared}
rownames(sponge.prop.df) = names(sponge.corrected.list)
sponge.prop.df <- sponge.prop.df[, c(1,3,2,4)]
sponge.prop.df[sponge.prop.df < 0] = 0
sponge.prop.df <- as.data.frame(t(apply(sponge.prop.df, 1,
function(x){x/sum(x)})))
partVar_plot(prop.df = sponge.prop.df)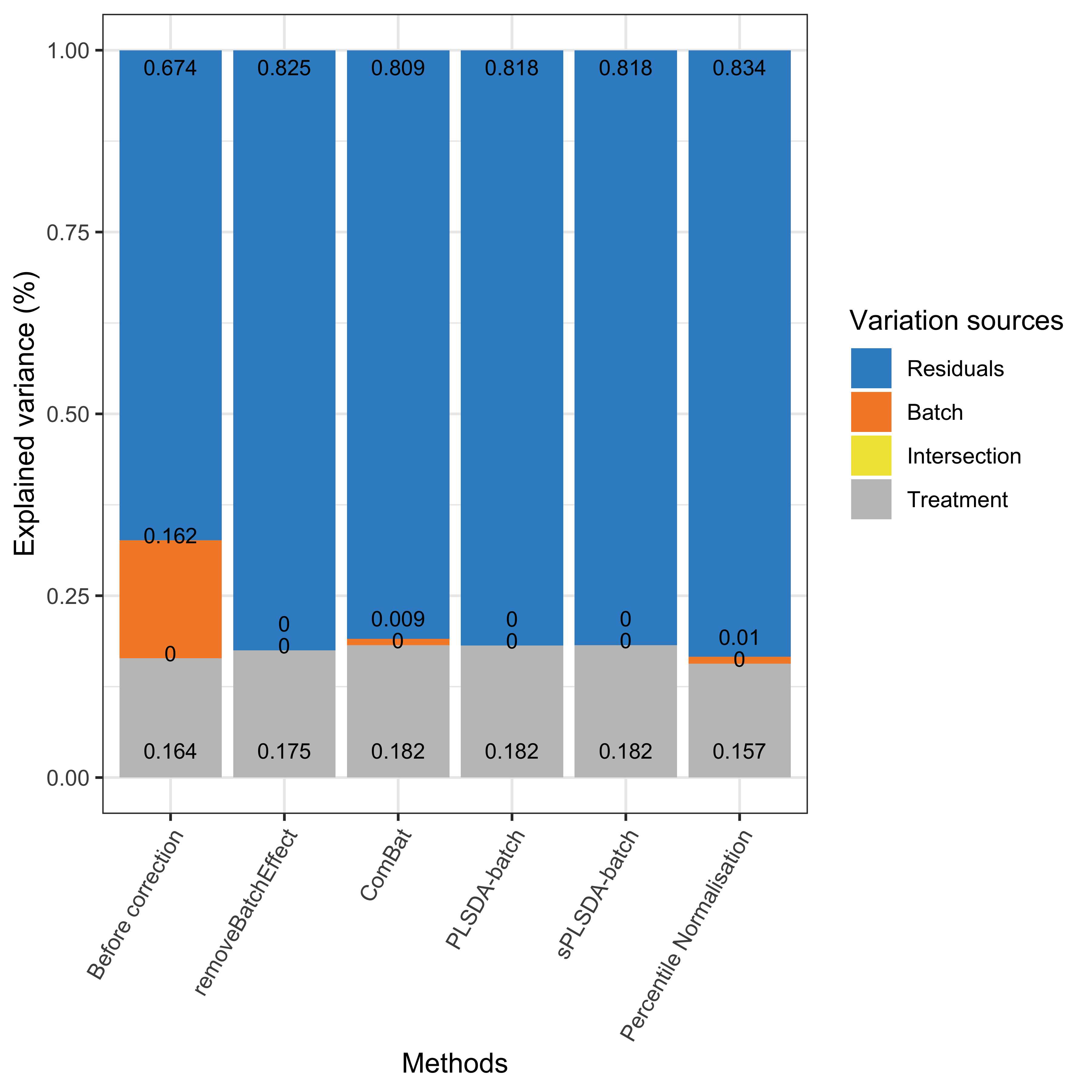
Figure 2.5: Global explained variance before and after batch effect correction for the sponge data.
As shown in the above figure, the intersection between batch and treatment variance was none for the sponge data, because the batch x treatment design is balanced. PLSDA-batch and sPLSDA-batch corrected data led to the best performance with a slightly higher proportion of explained treatment variance and no batch variance compared to the other methods.
2.1.4.2 Other methods
\(\mathbf{R^2}\)
The \(R^2\) values for each variable are calculated with lm() from stats package. To compare the \(R^2\) values among variables, we scale the corrected data before \(R^2\) calculation. The results are displayed with ggplot() from ggplot2 R package.
# scale
sponge.corr_scale.list <- lapply(sponge.corrected.list,
function(x){apply(x, 2, scale)})
sponge.r_values.list <- list()
for(i in 1:length(sponge.corr_scale.list)){
sponge.r_values <- data.frame(trt = NA, batch = NA)
for(c in 1:ncol(sponge.corr_scale.list[[i]])){
sponge.fit.res.trt <- lm(sponge.corr_scale.list[[i]][,c] ~ sponge.trt)
sponge.r_values[c,1] <- summary(sponge.fit.res.trt)$r.squared
sponge.fit.res.batch <- lm(sponge.corr_scale.list[[i]][,c] ~ sponge.batch)
sponge.r_values[c,2] <- summary(sponge.fit.res.batch)$r.squared
}
sponge.r_values.list[[i]] <- sponge.r_values
}
names(sponge.r_values.list) <- names(sponge.corr_scale.list)
sponge.boxp.list <- list()
for(i in seq_len(length(sponge.r_values.list))){
sponge.boxp.list[[i]] <-
data.frame(r2 = c(sponge.r_values.list[[i]][ ,'trt'],
sponge.r_values.list[[i]][ ,'batch']),
Effects = as.factor(rep(c('Treatment','Batch'),
each = 24)))
}
names(sponge.boxp.list) <- names(sponge.r_values.list)
sponge.r2.boxp <- rbind(sponge.boxp.list$`Before correction`,
sponge.boxp.list$removeBatchEffect,
sponge.boxp.list$ComBat,
sponge.boxp.list$`PLSDA-batch`,
sponge.boxp.list$`sPLSDA-batch`,
sponge.boxp.list$`Percentile Normalisation`,
sponge.boxp.list$RUVIII)
sponge.r2.boxp$methods <- rep(c('Before correction', ' removeBatchEffect',
'ComBat','PLSDA-batch', 'sPLSDA-batch',
'Percentile Normalisation'), each = 48)
sponge.r2.boxp$methods <- factor(sponge.r2.boxp$methods,
levels = unique(sponge.r2.boxp$methods))
ggplot(sponge.r2.boxp, aes(x = Effects, y = r2, fill = Effects)) +
geom_boxplot(alpha = 0.80) +
theme_bw() +
theme(text = element_text(size = 18),
axis.title.x = element_blank(),
axis.title.y = element_blank(),
axis.text.x = element_text(angle = 60, hjust = 1, size = 18),
axis.text.y = element_text(size = 18),
panel.grid.minor.x = element_blank(),
panel.grid.major.x = element_blank(),
legend.position = "right") + facet_grid( ~ methods) +
scale_fill_manual(values=pb_color(c(12,14))) 
Figure 2.6: Sponge study: \(R^2\) values for each microbial variable before and after batch effect correction.
We observed that the data corrected by ComBat, percentile normalisation still included a few variables with a large proportion of batch variance as shown in the above figures.
##################################
sponge.barp.list <- list()
for(i in seq_len(length(sponge.r_values.list))){
sponge.barp.list[[i]] <-
data.frame(r2 = c(sum(sponge.r_values.list[[i]][ ,'trt']),
sum(sponge.r_values.list[[i]][ ,'batch'])),
Effects = c('Treatment','Batch'))
}
names(sponge.barp.list) <- names(sponge.r_values.list)
sponge.r2.barp <- rbind(sponge.barp.list$`Before correction`,
sponge.barp.list$removeBatchEffect,
sponge.barp.list$ComBat,
sponge.barp.list$`PLSDA-batch`,
sponge.barp.list$`sPLSDA-batch`,
sponge.barp.list$`Percentile Normalisation`,
sponge.barp.list$RUVIII)
sponge.r2.barp$methods <- rep(c('Before correction', ' removeBatchEffect',
'ComBat','PLSDA-batch', 'sPLSDA-batch',
'Percentile Normalisation'), each = 2)
sponge.r2.barp$methods <- factor(sponge.r2.barp$methods,
levels = unique(sponge.r2.barp$methods))
ggplot(sponge.r2.barp, aes(x = Effects, y = r2, fill = Effects)) +
geom_bar(stat="identity") +
theme_bw() +
theme(text = element_text(size = 18),
axis.title.x = element_blank(),
axis.title.y = element_blank(),
axis.text.x = element_text(angle = 60, hjust = 1, size = 18),
axis.text.y = element_text(size = 18),
panel.grid.minor.x = element_blank(),
panel.grid.major.x = element_blank(),
legend.position = "right") + facet_grid( ~ methods) +
scale_fill_manual(values=pb_color(c(12,14)))
Figure 2.7: Sponge study: the sum of \(R^2\) values for each microbial variable before and after batch effect correction.
When considering the sum of all variables, the remaining batch variance of corrected data from sPLSDA-batch was similar as PLSDA-batch, which was greater than removeBatchEffect. The preserved treatment variance of corrected data from sPLSDA-batch was also similar as PLSDA-batch which was greater than removeBatchEffect.
Alignment scores
To use the alignment_score() function from PLSDAbatch, we need to specify the proportion of data variance to explain (var), the number of nearest neighbours (k) and the number of principal components to estimate (ncomp). We then use ggplot() function from ggplot2 to visualise the results.
sponge.var = 0.95
sponge.k = 3
sponge.scores <- c()
for(i in 1:length(sponge.corrected.list)){
res <- alignment_score(data = sponge.corrected.list[[i]],
batch = sponge.batch,
var = sponge.var,
k = sponge.k,
ncomp = 20)
sponge.scores <- c(sponge.scores, res)
}
sponge.scores.df <- data.frame(scores = sponge.scores,
methods = names(sponge.corrected.list))
sponge.scores.df$methods <- factor(sponge.scores.df$methods,
levels = rev(names(sponge.corrected.list)))
ggplot() + geom_col(aes(x = sponge.scores.df$methods,
y = sponge.scores.df$scores)) +
geom_text(aes(x = sponge.scores.df$methods,
y = sponge.scores.df$scores/2,
label = round(sponge.scores.df$scores, 3)),
size = 3, col = 'white') +
coord_flip() + theme_bw() + ylab('Alignment Scores') +
xlab('') + ylim(0,0.4)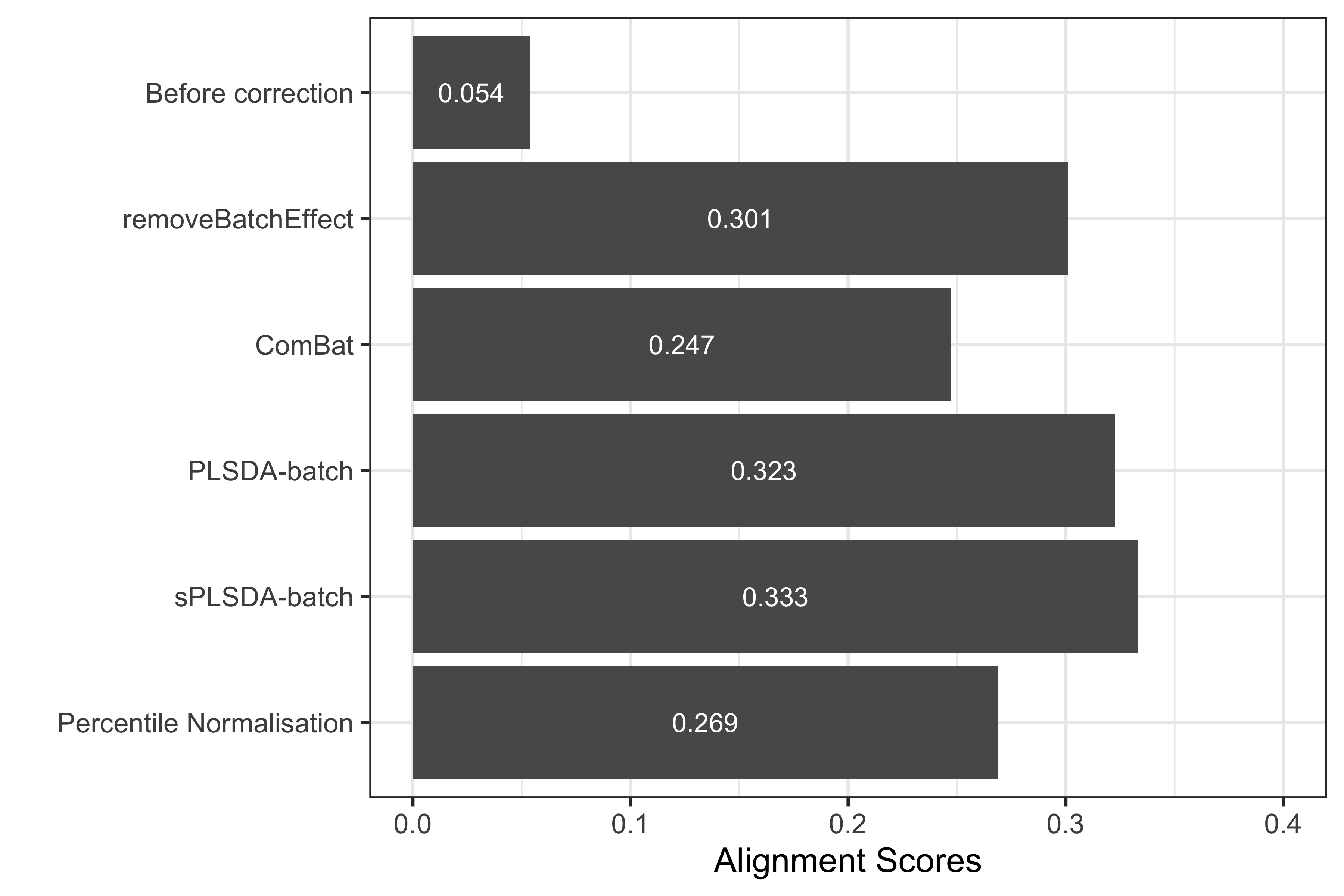
Figure 2.8: Comparison of alignment scores before and after batch effect correction using different methods for the sponge data.
The alignment scores complement the PCA results, especially when batch effect removal is difficult to assess on PCA sample plots. Since a higher alignment score indicates that samples are better mixed, as shown in the above figure, sPLSDA-batch gave a superior performance compared to the other methods.
Variable selection
We use splsda() from mixOmics to select the top 5 microbial variables that, in combination, discriminate the different treatment groups in the sponge data. We apply splsda() to the different batch effect corrected data from all methods. Then we use upset() from UpSetR package (Lex et al. 2014) to visualise the concordance of variables selected.
In the code below, we first need to convert the list of variables selected from different method-corrected data into a data frame compatible with upset() using fromList(). We then assign different colour schemes for each variable selection.
sponge.splsda.select <- list()
for(i in 1:length(sponge.corrected.list)){
splsda.res <- splsda(X = sponge.corrected.list[[i]],
Y = sponge.trt,
ncomp = 3, keepX = rep(5,3))
select.res <- selectVar(splsda.res, comp = 1)$name
sponge.splsda.select[[i]] <- select.res
}
names(sponge.splsda.select) <- names(sponge.corrected.list)
# can only visualise 5 methods
sponge.splsda.select <- sponge.splsda.select[c(1:5)]
sponge.splsda.upsetR <- fromList(sponge.splsda.select)
upset(sponge.splsda.upsetR, main.bar.color = 'gray36',
sets.bar.color = pb_color(c(25:22,20)), matrix.color = 'gray36',
order.by = 'freq', empty.intersections = 'on',
queries =
list(list(query = intersects, params = list('Before correction'),
color = pb_color(20), active = T),
list(query = intersects, params = list('removeBatchEffect'),
color = pb_color(22), active = T),
list(query = intersects, params = list('ComBat'),
color = pb_color(23), active = T),
list(query = intersects, params = list('PLSDA-batch'),
color = pb_color(24), active = T),
list(query = intersects, params = list('sPLSDA-batch'),
color = pb_color(25), active = T)))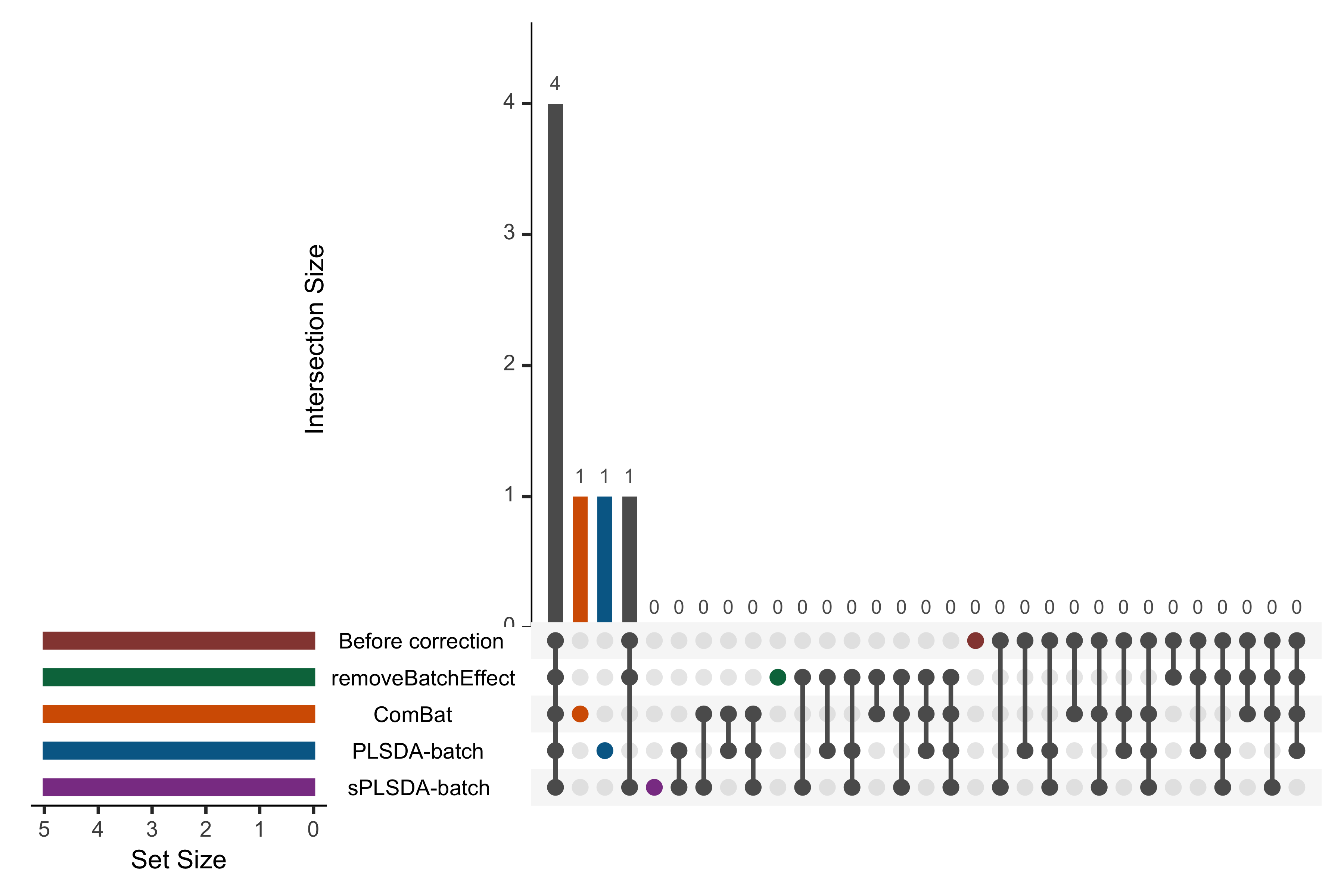
Figure 2.9: UpSet plot showing overlap between variables selected from different corrected data for the sponge study.
In the above figure, the left bars indicate the number of variables selected from each data corrected with different methods. The right bar plot combined with the scatterplot show different intersection and their aggregates. We obtained an overlap of 4 out of 5 selected variables between different corrected and uncorrected data. However, the data from each method still included unique variables that were not selected in the other corrected data, e.g., ComBat and PLSDA-batch. As upset() can only include five datasets at once, we only displayed the uncorrected data and four corrected data that had been more efficiently corrected for batch effects from our previous assessments compared to the other datasets.
2.2 HFHS data
2.2.1 Data pre-processing
2.2.1.1 Prefiltering
We load the HFHS data stored internally with function data().
load(file = './data/HFHS_data.rda')
hfhs.count <- HFHS_data$FullData$X.count
dim(hfhs.count)## [1] 250 4524hfhs.filter.res <- PreFL(data = hfhs.count)
hfhs.filter <- hfhs.filter.res$data.filter
dim(hfhs.filter)## [1] 250 515# zero proportion before filtering
hfhs.filter.res$zero.prob## [1] 0.8490805# zero proportion after filtering
sum(hfhs.filter == 0)/(nrow(hfhs.filter) * ncol(hfhs.filter))## [1] 0.2955184The raw HFHS data include 4524 OTUs and 250 samples. We use the function PreFL() from our PLSDAbatch R package to filter the data. After filtering, the HFHS data were reduced to 515 OTUs and 250 samples. The proportion of zeroes was reduced from 85% to 30%.
2.2.1.2 Transformation
Prior to CLR transformation, we recommend adding 1 as the offset for the HFHS data - that are raw count data. We use logratio.transfo() function in mixOmics package to CLR transform the data.
hfhs.clr <- logratio.transfo(X = hfhs.filter, logratio = 'CLR', offset = 1)
class(hfhs.clr) <- 'matrix'2.2.2 Batch effect detection
2.2.2.1 PCA
We apply pca() function from mixOmics package to the HFHS data and use Scatter_Density() function from PLSDAbatch to represent the PCA sample plot with densities.
hfhs.pca.before <- pca(hfhs.clr, ncomp = 3, scale = TRUE)
hfhs.metadata <- HFHS_data$FullData$metadata
rownames(hfhs.metadata) <- hfhs.metadata$SampleID
hfhs.metadata <- hfhs.metadata[rownames(hfhs.clr),]
hfhs.cage <- as.factor(hfhs.metadata$DietCage)
hfhs.day <- as.factor(hfhs.metadata$Day)
hfhs.trt <- as.factor(hfhs.metadata$Diet)
names(hfhs.cage) = names(hfhs.day) = names(hfhs.trt) = hfhs.metadata$SampleID
hfhs.pca.before.cage.plot <-
Scatter_Density(object = hfhs.pca.before,
batch = hfhs.cage,
trt = hfhs.trt,
title = 'HFHS data',
trt.legend.title = 'Diet',
batch.legend.title = 'Cage')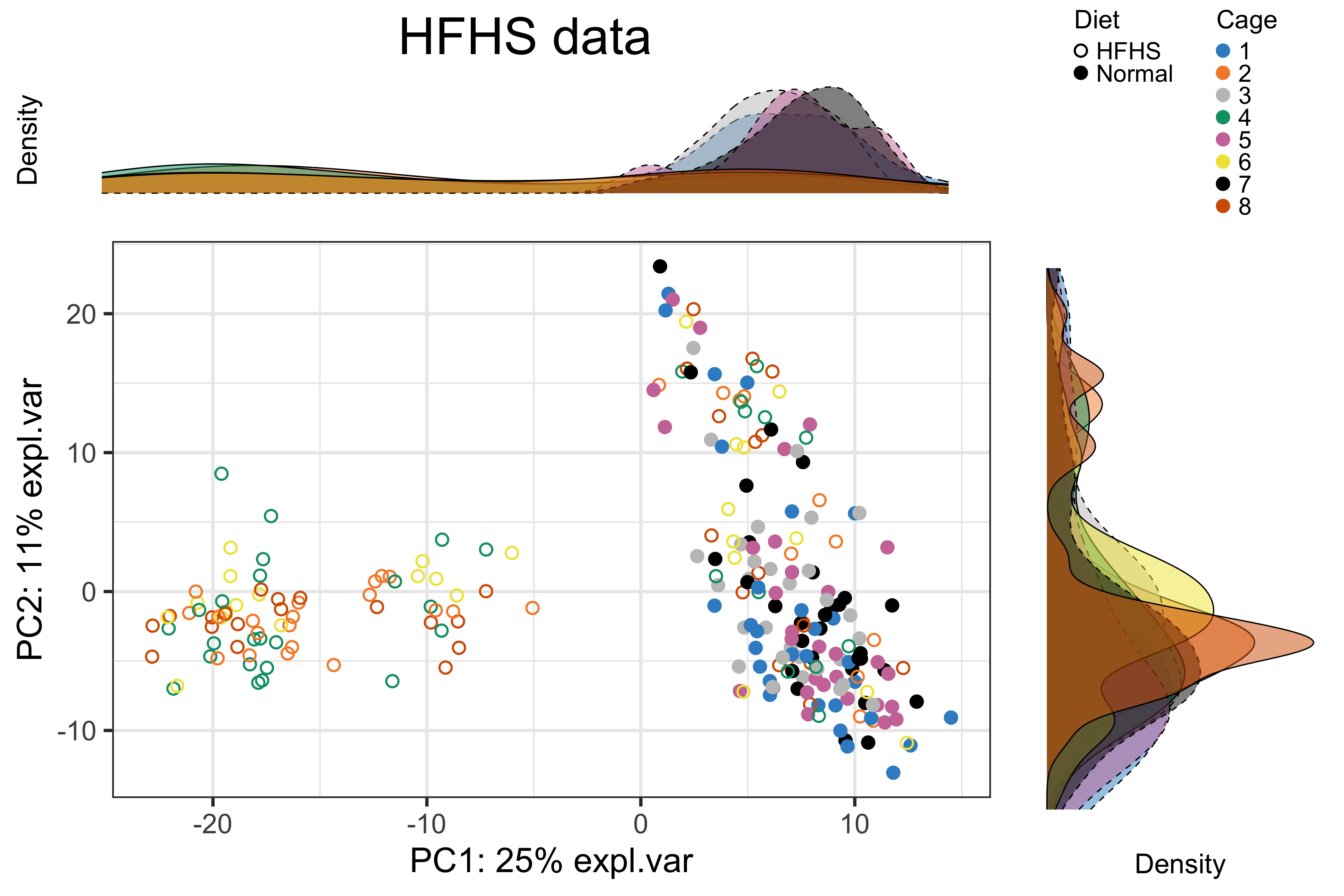
Figure 2.10: The PCA sample plot with densities coloured by cages in the HFHS data.
In the above figure, part of the samples with different diets were mixed together, while all the samples from different batches (i.e., cages) were well mixed and not distinct. This result indicates no cage effect for the whole data and no treatment effect for part of samples.
hfhs.pca.before.day.plot <-
Scatter_Density(object = hfhs.pca.before,
batch = hfhs.day,
trt = hfhs.trt,
title = 'HFHS data',
trt.legend.title = 'Diet',
batch.legend.title = 'Day')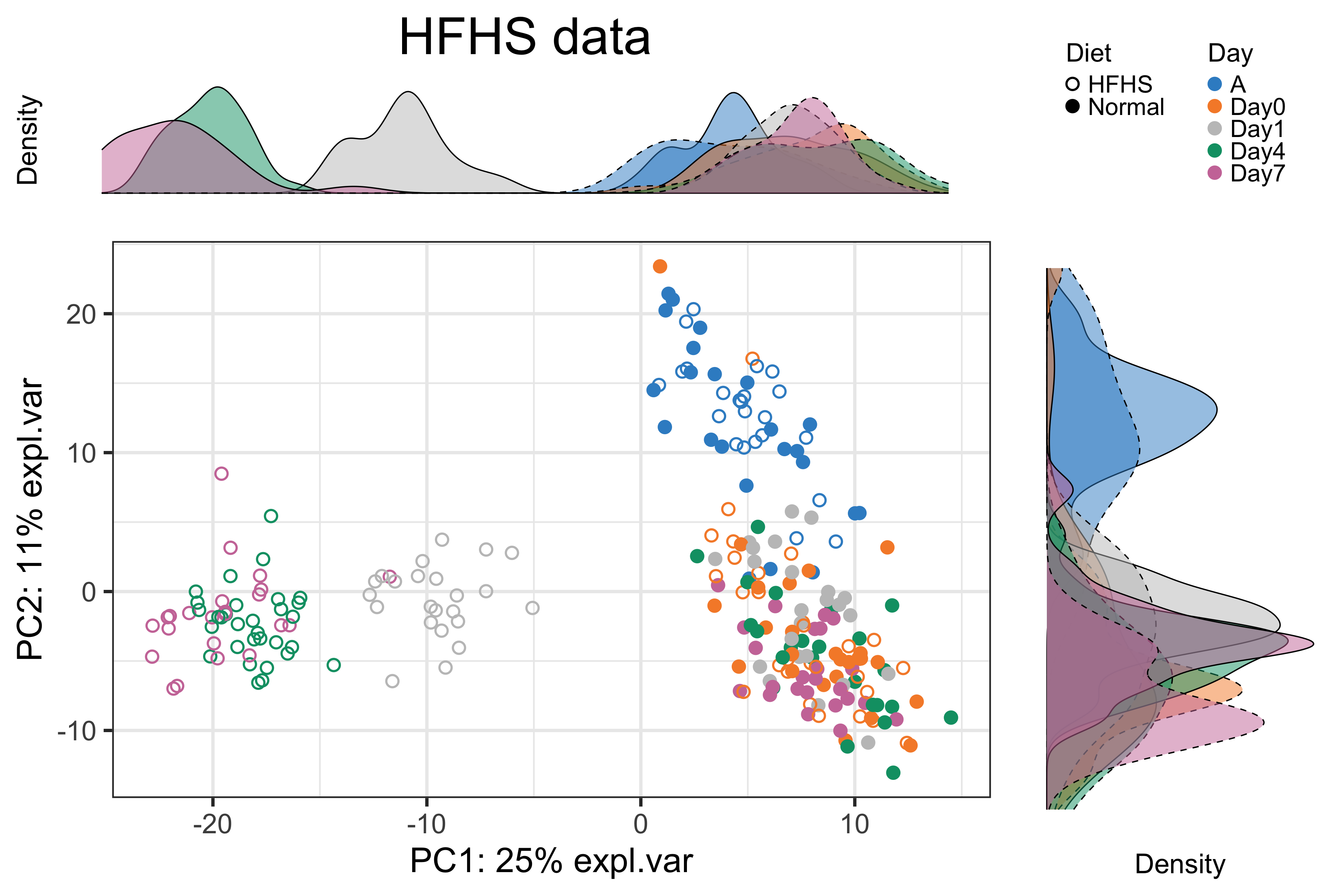
Figure 2.11: Figure 11: The PCA sample plot with densities coloured by days in the HFHS data.
As shown in the above figure, we did not observe a difference between samples with different diets on arrival day “A” and “Day0”. This result was consistent with the experimental design, as mice were not treated with different diets on these two days. We thus removed the samples from these two days.
# remove samples from arrival day and day0
hfhs.dA0.idx <- c(which(hfhs.day == 'A'), which(hfhs.day == 'Day0'))
hfhs.clr.less <- hfhs.clr[-hfhs.dA0.idx,]
hfhs.metadata.less <- hfhs.metadata[-hfhs.dA0.idx,]
hfhs.cage.less <- as.factor(hfhs.metadata.less$DietCage)
hfhs.day.less <- as.factor(hfhs.metadata.less$Day)
hfhs.trt.less <- as.factor(hfhs.metadata.less$Diet)
names(hfhs.cage.less) = names(hfhs.day.less) =
names(hfhs.trt.less) = hfhs.metadata.less$SampleID
hfhs.less.pca.before <- pca(hfhs.clr.less, ncomp = 3, scale = TRUE)
hfhs.less.pca.before.cage.plot <-
Scatter_Density(object = hfhs.less.pca.before,
batch = hfhs.cage.less,
trt = hfhs.trt.less,
title = 'HFHS data',
trt.legend.title = 'Diet',
batch.legend.title = 'Cage')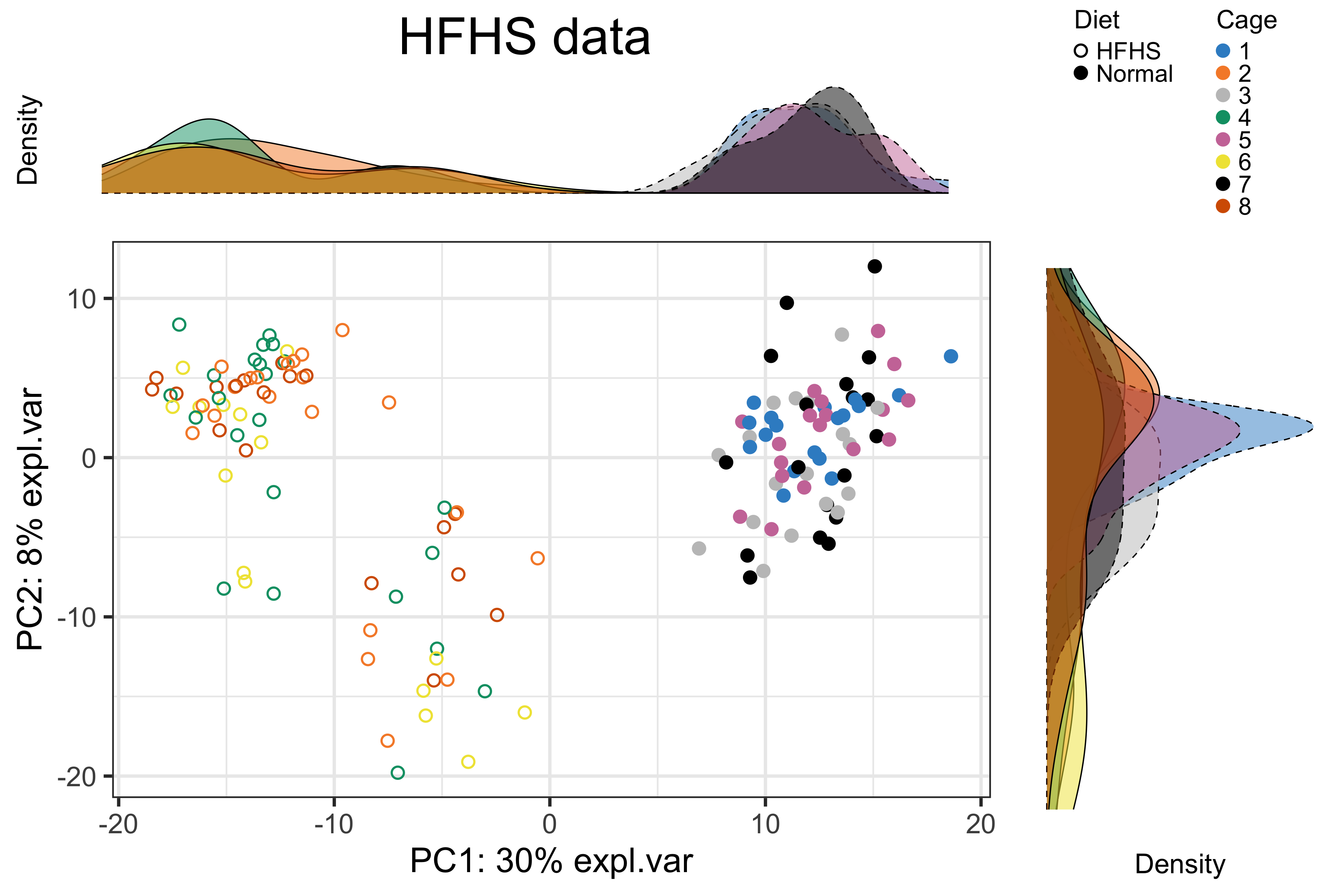
Figure 2.12: The PCA sample plot with densities coloured by cages in the reduced HFHS data.
hfhs.less.pca.before.day.plot <-
Scatter_Density(object = hfhs.less.pca.before,
batch = hfhs.day.less,
trt = hfhs.trt.less,
title = 'HFHS data',
trt.legend.title = 'Diet',
batch.legend.title = 'Day')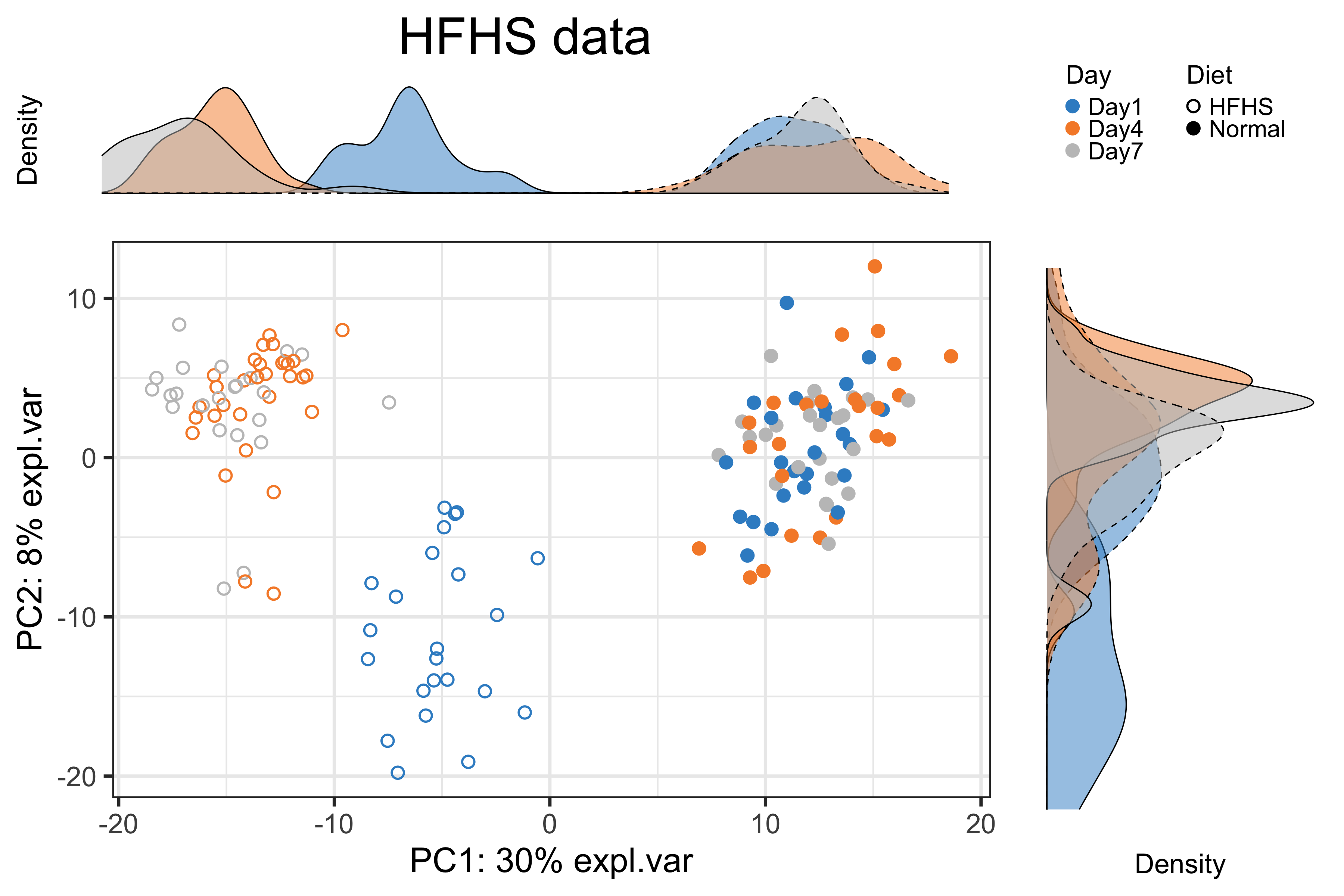
Figure 2.13: The PCA sample plot with densities coloured by days in the reduced HFHS data.
We observed a substantial diet variation on component 1, no cage variation, and a difference between samples collected on “Day1” and the other days with the HFHS diet as shown in the above figures.
2.2.2.2 Heatmap
We produce a heatmap using pheatmap package. The data first need to be scaled on both OTUs and samples.
# scale the clr data on both OTUs and samples
hfhs.clr.s <- scale(hfhs.clr.less, center = T, scale = T)
hfhs.clr.ss <- scale(t(hfhs.clr.s), center = T, scale = T)
# The cage effect
hfhs.anno_col <- data.frame(Cage = hfhs.cage.less,
Day = hfhs.day.less,
Treatment = hfhs.trt.less)
hfhs.anno_colors <- list(Cage = color.mixo(1:8),
Day = color.mixo(1:3),
Treatment = pb_color(1:2))
names(hfhs.anno_colors$Cage) = levels(hfhs.cage.less)
names(hfhs.anno_colors$Day) = levels(hfhs.day.less)
names(hfhs.anno_colors$Treatment) = levels(hfhs.trt.less)
pheatmap(hfhs.clr.ss,
cluster_rows = F,
fontsize_row = 4,
fontsize_col = 6,
fontsize = 8,
clustering_distance_rows = 'euclidean',
clustering_method = 'ward.D',
treeheight_row = 30,
annotation_col = hfhs.anno_col,
annotation_colors = hfhs.anno_colors,
border_color = 'NA',
main = 'HFHS data - Scaled')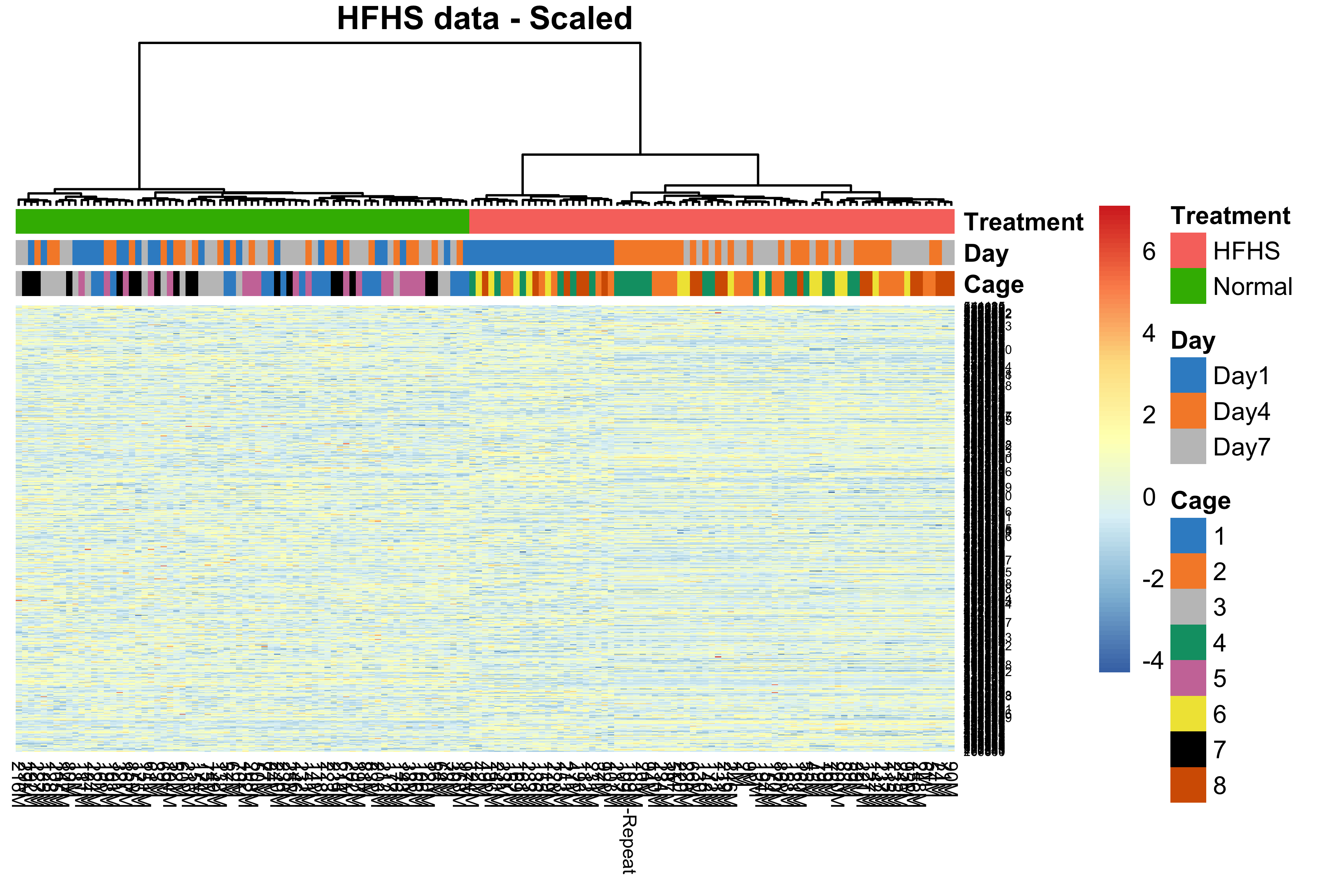
Figure 2.14: Hierarchical clustering for samples in the HFHS data.
In the above figure, samples in the HFHS data were clustered according to the treatments not cages, indicating no cage effect and a strong treatment effect. Samples from the batch “Day1” were clustered and distinct from the other batches with diet HFHS but not the normal diet, indicating a day effect but very weak.
2.2.2.3 pRDA
We apply pRDA with varpart() function from vegan R package.
hfhs.factors.df <- data.frame(trt = hfhs.trt.less,
cage = hfhs.cage.less,
day = hfhs.day.less)
hfhs.rda.cage.before <- varpart(hfhs.clr.less, ~ trt, ~ cage,
data = hfhs.factors.df, scale = T)
hfhs.rda.cage.before$part$indfract## Df R.squared Adj.R.squared Testable
## [a] = X1|X2 0 NA -2.220446e-16 FALSE
## [b] = X2|X1 6 NA 1.277627e-02 TRUE
## [c] 0 NA 2.713111e-01 FALSE
## [d] = Residuals NA NA 7.159126e-01 FALSEIn the result, X1 and X2 represent the first and second covariates fitted in the model. [a], [b] represent the independent proportion of variance explained by X1 and X2 respectively, and [c] represents the intersection variance shared between X1 and X2. In the HFHS data, the cage and diet effects have a nested batch x treatment design that is extremely unbalanced. We didn’t detect any treatment variance (indicated in line [a], Adj.R.squared = 0) but considerable intersection variance (indicated in line [c], Adj.R.squared = 0.271). Thus, all the treatment variance was explained by the intersection variance shared with batch variance. It means batch and treatment effects are collinear. Therefore, the cage effect in the HFHS data can only be accounted for with a linear mixed model, as detailed in section accounting for batch effects method “Linear regression”.
hfhs.rda.day.before <- varpart(hfhs.clr.less, ~ trt, ~ day,
data = hfhs.factors.df, scale = T)
hfhs.rda.day.before$part$indfract## Df R.squared Adj.R.squared Testable
## [a] = X1|X2 1 NA 0.2721810304 TRUE
## [b] = X2|X1 2 NA 0.0361767632 TRUE
## [c] 0 NA -0.0008699296 FALSE
## [d] = Residuals NA NA 0.6925121361 FALSEFor the day and diet effects, the batch x treatment design is balanced. There was no intersection variance (indicated in line [c], Adj.R.squared = 0). The proportion of treatment variance was much higher than batch variance as indicated in lines [a] (Adj.R.squared = 0.272) and [b] (Adj.R.squared = 0.036).
2.2.3 Managing batch effects
2.2.3.1 Accounting for batch effects
The methods that we use to account for batch effects include the methods designed for microbiome data: zero-inflated Gaussian (ZIG) mixture model and the methods adapted for microbiome data: linear regression, SVA and RUV4. Among them, SVA and RUV4 are designed for unknown batch effects.
Methods designed for microbiome data
Zero-inflated Gaussian mixture model To use the ZIG model, we first create a MRexperiment object applying newMRexperiment() (from metagenomeSeq package) to microbiome counts and annotated data frames with metadata and taxonomic information generated with AnnotatedDataFrame() from Biobase package.
# Creating a MRexperiment object (make sure no NA in metadata)
rownames(HFHS_data$FullData$metadata) <- rownames(HFHS_data$FullData$X.count)
HFHS.phenotypeData =
AnnotatedDataFrame(data = HFHS_data$FullData$metadata[-hfhs.dA0.idx,])
HFHS.taxaData =
AnnotatedDataFrame(data = as.data.frame(HFHS_data$FullData$taxa))
HFHS.obj = newMRexperiment(counts =
t(HFHS_data$FullData$X.count[-hfhs.dA0.idx,]),
phenoData = HFHS.phenotypeData,
featureData = HFHS.taxaData)
HFHS.obj## MRexperiment (storageMode: environment)
## assayData: 4524 features, 149 samples
## element names: counts
## protocolData: none
## phenoData
## sampleNames: 109M 131M ... 39M (149 total)
## varLabels: SampleID MouseID ... Replicated (14 total)
## varMetadata: labelDescription
## featureData
## featureNames: 4333897 541135 ... 228232 (4524 total)
## fvarLabels: Kingdom Phylum ... Species (7 total)
## fvarMetadata: labelDescription
## experimentData: use 'experimentData(object)'
## Annotation:The HFHS data are then filtered with filterData() function (from metagenomeSeq). We can use MRcounts() to extract the count data from the MRexperiment object.
# filtering data to maintain a threshold of minimum depth or OTU presence
dim(MRcounts(HFHS.obj))## [1] 4524 149HFHS.obj = filterData(obj = HFHS.obj, present = 20, depth = 5)
dim(MRcounts(HFHS.obj))## [1] 1255 149After filtering, the HFHS data were reduced to 1255 OTUs and 149 samples.
We calculate the percentile for CSS normalisation with cumNormStatFast() function (from metagenomeSeq package). The CSS normalisation is applied with cumNorm() and the normalised data can be exported using MRcounts() with norm = TRUE. The normalisation scaling factors for each sample, which are the sum of counts up to the calculated percentile, can be accessed through normFactors(). We calculate the log transformed scaling factors by diving them with their median, which are better than the default scaling factors that are divided by 1000 (log2(normFactors(obj)/1000 + 1)).
# calculate the percentile for CSS normalisation
HFHS.pctl = cumNormStatFast(obj = HFHS.obj)
# CSS normalisation
HFHS.obj <- cumNorm(obj = HFHS.obj, p = HFHS.pctl)
# export normalised data
HFHS.norm.data <- MRcounts(obj = HFHS.obj, norm = TRUE)
# normalisation scaling factors for each sample
HFHS.normFactor = normFactors(object = HFHS.obj)
HFHS.normFactor = log2(HFHS.normFactor/median(HFHS.normFactor) + 1)As the ZIG model applies a linear model, the cage effect cannot be fitted. Moreover, the cage effect is very weak which only accounted for 1.3% of the total data variance calculated with pRDA. Thus we only fit and account for the day effect. We create a design matrix with treatment variable (Diet_effect), batch variable (Day_effect) and the log transformed scaling factors by using model.matrix(), and then apply the ZIG model by fitZig() function. We set useCSSoffset = FALSE to avoid using the default scaling factors as we have already included our customised scaling factor (HFHS.normFactor) in the design matrix.
# treatment variable
Diet_effect = pData(object = HFHS.obj)$Diet
# batch variable
Day_effect = pData(object = HFHS.obj)$Day
# build a design matrix
HFHS.mod.full = model.matrix(~ Diet_effect + Day_effect + HFHS.normFactor)
# settings for the fitZig() function
HFHS.settings <- zigControl(maxit = 10, verbose = TRUE)
# apply the ZIG model
HFHSfit <- fitZig(obj = HFHS.obj, mod = HFHS.mod.full,
useCSSoffset = FALSE, control = HFHS.settings)## it= 0, nll=236.34, log10(eps+1)=Inf, stillActive=1255
## it= 1, nll=256.75, log10(eps+1)=0.06, stillActive=203
## it= 2, nll=255.94, log10(eps+1)=0.04, stillActive=153
## it= 3, nll=256.56, log10(eps+1)=0.04, stillActive=47
## it= 4, nll=257.05, log10(eps+1)=0.01, stillActive=11
## it= 5, nll=257.28, log10(eps+1)=0.01, stillActive=3
## it= 6, nll=257.39, log10(eps+1)=0.02, stillActive=2
## it= 7, nll=257.46, log10(eps+1)=0.00, stillActive=0The OTUs with the top 50 smallest p values are extracted using MRcoefs(). We set eff = 0.5, so only the OTUs with at least “0.5” quantile (50%) number of effective samples (positive samples + estimated undersampling zeroes) are extracted.
HFHScoefs <- MRcoefs(HFHSfit, coef = 2, group = 3, number = 50, eff = 0.5)
head(HFHScoefs)## Diet_effectNormal pvalues adjPvalues
## 324926 1.0156067 7.360015e-11 9.236819e-08
## 337550 1.1730238 1.110138e-09 4.362904e-07
## 4353745 -0.7058975 1.212492e-09 4.362904e-07
## 357471 0.9636651 1.390567e-09 4.362904e-07
## 313499 -0.6093954 2.160477e-09 5.422797e-07
## 3940440 -0.7199750 5.150634e-09 1.077341e-06Other methods adapted for microbiome data
Linear regression Linear regression is conducted with linear_regres() function in PLSDAbatch. We integrated the performance package that assesses performance of regression models into our function linear_regres(). Therefore, we can apply check_model() from performance to the outputs from linear_regres() to diagnose the validity of the model fitted with treatment and batch effects for each variable (LÃŒdecke et al. 2020). We can extract performance measurements such as adjusted R2, RMSE, RSE, AIC and BIC for the models fitted with and without batch effects, which are also the outputs of linear_regres().
To deal with the day effect only, we apply type = "linear model" because of the balanced batch x treatment design.
hfhs.lm <- linear_regres(data = hfhs.clr.less,
trt = hfhs.trt.less,
batch.fix = hfhs.day.less,
type = 'linear model')
hfhs.p <- sapply(hfhs.lm$lm.table, function(x){x$coefficients[2,4]})
hfhs.p.adj <- p.adjust(p = hfhs.p, method = 'fdr')
check_model(hfhs.lm$model$`541135`)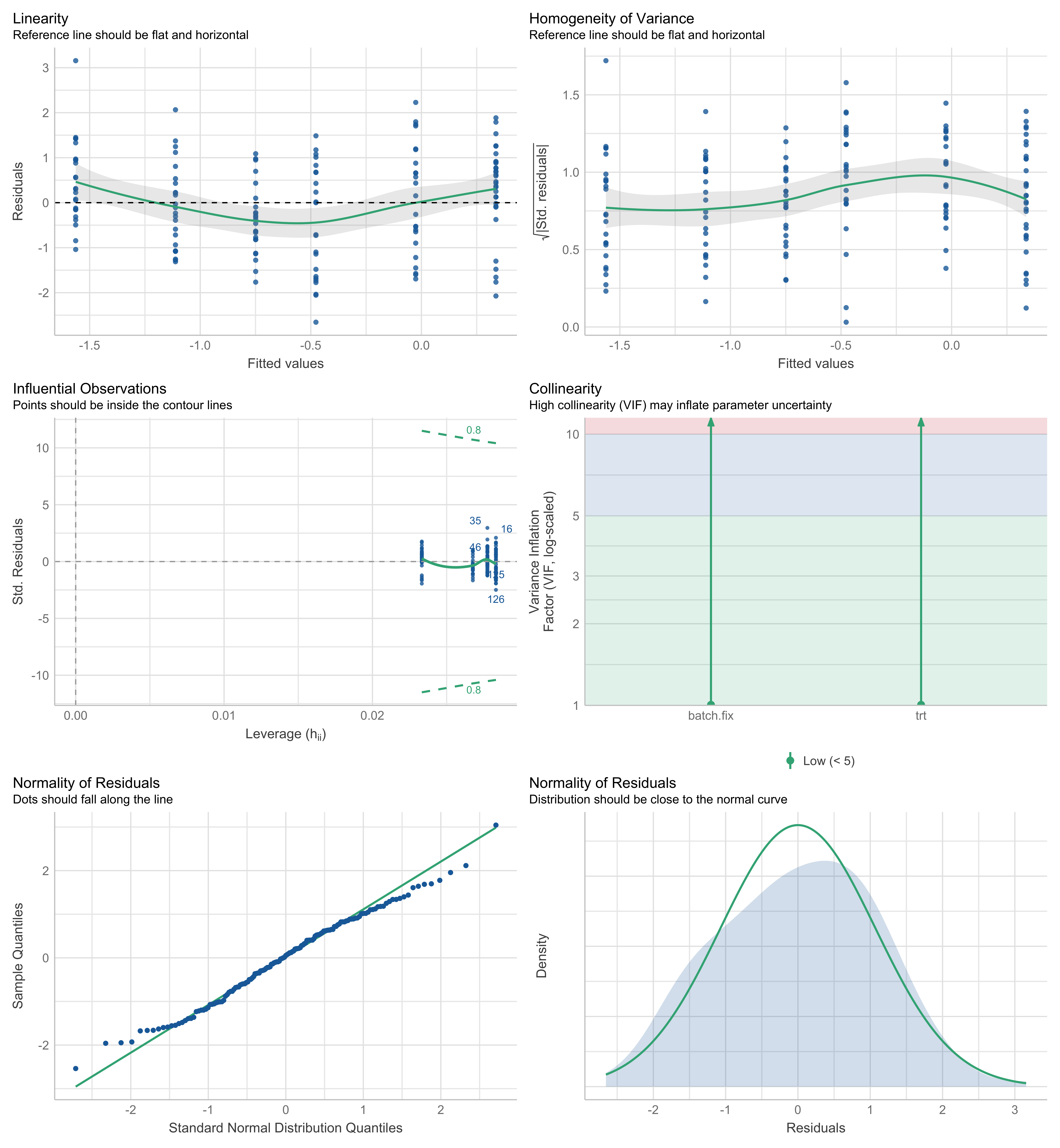
Figure 2.15: Diagnostic plots for the model fitted with the day effect of “OTU 541135” in the HFHS data.
To diagnose the validity of the model fitted with both treatment and batch effects, we use different plots to check the assumptions of each microbial variable. For example, the diagnostic plots of “OTU 541135” are shown in the above figure panel. The simulated data under the fitted model were not very close to the real data (shown as green line), indicating an imperfect fitness (top panel). The linearity (or homoscedasticity) and homogeneity of variance were not satisfied. The correlation between batch (batch.fix) and treatment (trt) effects was very low, indicating a good model with low collinearity. Some samples could be classified as outliers with a Cook’s distance larger than or equal to 0.5, for example, “46”, “35”, “126”, “125” and “16” (middle panel). The distribution of residuals was very close to normal (bottom panel). For the microbial variables with some assumptions not met, we should be careful about their results.
For performance measurements of models fitted with or without batch effects, We show an example of the results for some variables.
head(hfhs.lm$adj.R2)## trt.only trt.batch
## 541135 0.1969688 0.2590190
## 276629 0.6419160 0.6414949
## 196070 0.1618319 0.1530262
## 318732 0.1720195 0.1795344
## 339886 0.1542615 0.1779073
## 337724 0.2343320 0.2445358If the adjusted \(R^2\) of the model with both treatment and batch effects is larger than the model with treatment effects only, e.g., OTU 541135, the model fitted with batch effects explains more data variance, and is thus better than the model without batch effects. Otherwise, the batch effect is not necessary to be added into the linear model.
We next look at the AIC of models fitted with or without batch effects.
head(hfhs.lm$AIC)## trt.only trt.batch
## 541135 462.0799 452.0564
## 276629 294.7536 296.8876
## 196070 504.2549 507.7710
## 318732 462.8639 463.4643
## 339886 248.0616 245.7953
## 337724 424.2142 424.1741A lower AIC indicates a better fit. Both results were mostly consistent on model selection, except “OTU318732”. Based on adjusted \(R^2\), we needed to include batch effects, while based on AIC, we should not. Therefore, we needed more measurements such as BIC, RSE.
To consider the cage effect only or the cage and day effects together, we apply type = "linear mixed model" to the HFHS data because of the nested batch x treatment design for the cage effect.
hfhs.lmm <- linear_regres(data = hfhs.clr.less,
trt = hfhs.trt.less,
batch.fix = hfhs.day.less,
batch.random = hfhs.cage.less,
type = 'linear mixed model')hfhs.p <- sapply(hfhs.lmm$lmm.table, function(x){x$coefficients[2,5]})
hfhs.p.adj <- p.adjust(p = hfhs.p, method = 'fdr')
check_model(hfhs.lmm$model$`541135`)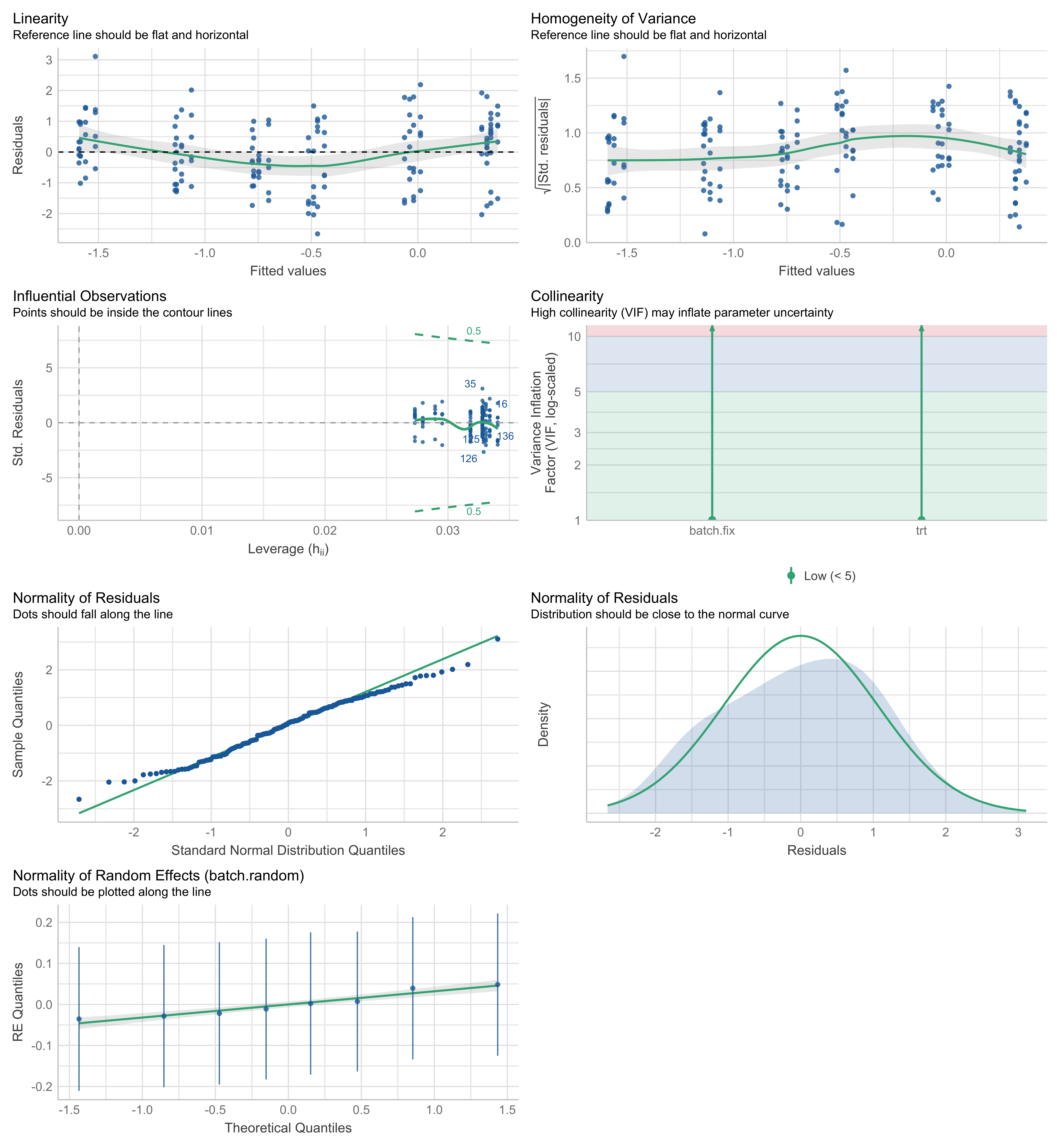
Figure 2.16: Diagnostic plots for the model fitted with the day and cage effects of “OTU541135” in the HFHS data.
According to the diagnostic plots of “OTU541135” as shown in the above figure panel, The simulated data under the fitted model were not very close to the real data (shown as green line), indicating an imperfect fitness (top panel). The linearity (or homoscedasticity) and homogeneity of variance were not satisfied. The correlation between batch (batch.fix) and treatment (trt) effects was very low, indicating a good model with low collinearity. Some samples could be classified as outliers with a Cook’s distance larger than or equal to 0.5, for example, “16”, “35”, “126”, “125” and “136” (middle panel). The distribution of residuals and random effects was very close to normal (bottom panel).
For performance measurements of models fitted with or without batch effects, We show an example of the results for some variables.
head(hfhs.lmm$AIC)## trt.only trt.batch
## 541135 462.0799 461.4074
## 276629 294.7536 310.3455
## 196070 504.2549 515.0180
## 318732 462.8639 472.5556
## 339886 248.0616 260.7115
## 337724 424.2142 432.9937For some OTUs, the model fitted without batch effects was better with a lower AIC. For example, “OTU276629”, “OTU196070”, “OTU318732”, “OTU339886” and “OTU337724”. “OTU541135” was more appropriate within a model with batch effects.
Since we apply a "linear mixed model" to the HFHS data, this type of model can only output conditional \(R^2\) that includes the variance of both fixed and random effects (treatment, fixed and random batch effects) and marginal \(R^2\) that includes only the variance of fixed effects (treatment and fixed batch effects) (Nakagawa and Schielzeth 2013).
head(hfhs.lmm$cond.R2)## trt.only trt.batch
## 541135 0.2023947 0.2748381
## 276629 0.6443355 0.6475581
## 196070 0.1674952 0.1932495
## 318732 0.1776140 NA
## 339886 0.1599760 0.1954862
## 337724 0.2395055 0.2845443head(hfhs.lmm$marg.R2)## trt.only trt.batch
## 541135 0.2023947 0.2692818
## 276629 0.6443355 0.6435223
## 196070 0.1674952 0.1678637
## 318732 0.1776140 0.1929564
## 339886 0.1599760 0.1916296
## 337724 0.2395055 0.2520680We observed that some variables resulted in singular fits (error message: Can't compute random effect variances. Some variance components equal zero. Your model may suffer from singulariy.) and the conditional \(R^2\)s of these variables were “NA”, which are expected to happen in linear mixed models when covariates are nested. We recommend noting the variables for which this error occurs, as it may lead to unreliable results.
SVA
SVA accounts for unknown batch effects. Here we assume that the batch grouping information in the HFHS data is unknown. We first build two design matrices with (hfhs.mod) and without (hfhs.mod0) treatment grouping information generated with model.matrix() function from stats. We then use num.sv() from sva package to determine the number of batch variables n.sv that will be used to estimate batch effects in function sva().
# estimate batch matrix
hfhs.mod <- model.matrix( ~ hfhs.trt.less)
hfhs.mod0 <- model.matrix( ~ 1, data = hfhs.trt.less)
hfhs.sva.n <- num.sv(dat = t(hfhs.clr.less), mod = hfhs.mod,
method = 'leek')
hfhs.sva <- sva(t(hfhs.clr.less), hfhs.mod, hfhs.mod0, n.sv = hfhs.sva.n)## Number of significant surrogate variables is: 1
## Iteration (out of 5 ):1 2 3 4 5The estimated batch effects are then applied to f.pvalue() to calculate the P-values of treatment effects. The estimated batch effects in SVA are assumed to be independent of the treatment effects. However, SVA considers some correlation between batch and treatment effects (Y. Wang and LêCao 2020).
# include estimated batch effects in the linear model
hfhs.mod.batch <- cbind(hfhs.mod, hfhs.sva$sv)
hfhs.mod0.batch <- cbind(hfhs.mod0, hfhs.sva$sv)
hfhs.sva.p <- f.pvalue(t(hfhs.clr.less), hfhs.mod.batch, hfhs.mod0.batch)
hfhs.sva.p.adj <- p.adjust(hfhs.sva.p, method = 'fdr')RUV4
Before applying RUV4 (RUV4() from ruv, we need to specify negative control variables and the number of batch variables to estimate. We can use the empirical negative controls that are not significantly differentially abundant (adjusted P > 0.05) from a linear regression with the treatment information as the only covariate.
We use a loop to fit a linear regression for each microbial variable and adjust P values of treatment effects for multiple comparisons with p.adjust() from stats. The empirical negative controls are then extracted according to the adjusted P values.
# empirical negative controls
hfhs.empir.p <- c()
for(e in 1:ncol(hfhs.clr.less)){
hfhs.empir.lm <- lm(hfhs.clr.less[,e] ~ hfhs.trt.less)
hfhs.empir.p[e] <- summary(hfhs.empir.lm)$coefficients[2,4]
}
hfhs.empir.p.adj <- p.adjust(p = hfhs.empir.p, method = 'fdr')
hfhs.nc <- hfhs.empir.p.adj > 0.05The number of batch variables k can be determined using getK() function.
# estimate k
hfhs.k.res <- getK(Y = hfhs.clr.less, X = hfhs.trt.less, ctl = hfhs.nc)
hfhs.k <- hfhs.k.res$k
hfhs.k <- ifelse(hfhs.k != 0, hfhs.k, 1)We then apply RUV4() with known treatment variables, estimated negative control variables and k batch variables. The calculated P values also need to be adjusted for multiple comparisons.
hfhs.ruv4 <- RUV4(Y = hfhs.clr.less, X = hfhs.trt.less,
ctl = hfhs.nc, k = hfhs.k)
hfhs.ruv4.p <- hfhs.ruv4$p
hfhs.ruv4.p.adj <- p.adjust(hfhs.ruv4.p, method = "fdr")Both SVA and RUV4 can account for both the cage and day effects, but not efficient at accounting for the cage effect, as the estimated surrogate batch effect in SVA and negative controls in RUV4 may not capture all the batch variation because of the nested batch x treatment design of the cage effect in the HFHS data.
2.2.3.2 Correcting for batch effects
The methods that we use to correct for batch effects include removeBatchEffect, ComBat, PLSDA-batch, sPLSDA-batch, Percentile Normalisation and RUVIII. Among them, RUVIII is designed for unknown batch effects.
Since the cage effect cannot be corrected for because of the collinearity between the cage and treatment effects and the cage effect only accounted for a small amount of the total data variance (1.3% calculated with pRDA), so we only correct for the day effect in the HFHS data.
removeBatchEffect
The removeBatchEffect() function is implemented in limma package. The design matrix (design) with treatment grouping information can be generated with model.matrix() function from stats as shown in section accounting for batch effects method “SVA”.
Here we use removeBatchEffect() function with batch grouping information (batch) and treatment design matrix (design) to calculate batch effect corrected data hfhs.rBE.
hfhs.rBE <- t(removeBatchEffect(t(hfhs.clr.less), batch = hfhs.day.less,
design = hfhs.mod))ComBat
The ComBat() function (from sva package) is implemented as parametric or non-parametric correction with option par.prior. Under a parametric adjustment, we can assess the model’s validity with prior.plots = T (Leek et al. 2012).
Here we use a non-parametric correction (par.prior = F) with batch grouping information (batch) and treatment design matrix (mod) to calculate batch effect corrected data hfhs.ComBat.
hfhs.ComBat <- t(ComBat(t(hfhs.clr.less), batch = hfhs.day.less,
mod = hfhs.mod, par.prior = F))PLSDA-batch
The PLSDA_batch() function is implemented in PLSDAbatch package. To use this function, we need to specify the optimal number of components related to treatment (ncomp.trt) or batch effects (ncomp.bat).
Here in the HFHS data, we use plsda() from mixOmics with only treatment grouping information to estimate the optimal number of treatment components to preserve.
# estimate the number of treatment components
hfhs.trt.tune <- plsda(X = hfhs.clr.less, Y = hfhs.trt.less, ncomp = 5)
hfhs.trt.tune$prop_expl_var #1## $X
## comp1 comp2 comp3 comp4 comp5
## 0.29946816 0.06913457 0.04242662 0.02681544 0.02189936
##
## $Y
## comp1 comp2 comp3 comp4 comp5
## 1.00000000 0.07124125 0.03858356 0.02564995 0.01555355We choose the number that explains 100% variance in the outcome matrix Y, thus from the result, 1 component is enough to preserve the treatment information.
We then use PLSDA_batch() function with both treatment and batch grouping information to estimate the optimal number of batch components to remove.
# estimate the number of batch components
hfhs.batch.tune <- PLSDA_batch(X = hfhs.clr.less,
Y.trt = hfhs.trt.less,
Y.bat = hfhs.day.less,
ncomp.trt = 1, ncomp.bat = 10)
hfhs.batch.tune$explained_variance.bat #2## $X
## comp1 comp2 comp3 comp4 comp5 comp6 comp7
## 0.10753644 0.03608189 0.02988326 0.02634760 0.02728936 0.05015144 0.03120534
## comp8 comp9 comp10
## 0.02908653 0.02430653 0.02103238
##
## $Y
## comp1 comp2 comp3 comp4 comp5 comp6
## 0.4937952138 0.5062047862 0.5126429685 0.4867993776 0.0005576539 0.5083690943
## comp7 comp8 comp9 comp10
## 0.4789523528 0.0126785529 0.5103228185 0.4734938502sum(hfhs.batch.tune$explained_variance.bat$Y[1:2])## [1] 1Using the same criterion as choosing treatment components, we choose the number of batch components that explains 100% variance in the outcome matrix of batch. According to the result, 2 components are required to remove batch effects.
We then can correct for batch effects applying PLSDA_batch() with treatment, batch grouping information and corresponding optimal number of related components.
##########
hfhs.PLSDA_batch.res <- PLSDA_batch(X = hfhs.clr.less,
Y.trt = hfhs.trt.less,
Y.bat = hfhs.day.less,
ncomp.trt = 1, ncomp.bat = 2)
hfhs.PLSDA_batch <- hfhs.PLSDA_batch.res$X.nobatchsPLSDA-batch
We apply sPLSDA-batch using the same function PLSDA_batch() but we specify the number of variables to select on each component (usually only treatment-related components keepX.trt). To determine the optimal number of variables to select, we use tune.splsda() function from mixOmics package (Rohart et al. 2017) with all possible numbers of variables to select for each component (test.keepX).
# estimate the number of variables to select per treatment component
set.seed(777)
hfhs.test.keepX = c(seq(1, 10, 1), seq(20, 200, 10),
seq(250, 500, 50), 515)
hfhs.trt.tune.v <- tune.splsda(X = hfhs.clr.less,
Y = hfhs.trt.less,
ncomp = 1,
test.keepX = hfhs.test.keepX,
validation = 'Mfold',
folds = 4, nrepeat = 50)
hfhs.trt.tune.v$choice.keepX # 2## comp1
## 2Here the optimal number of variables to select for the treatment component is 2. Since we adjust the amount of treatment variation to preserve, we need to re-choose the optimal number of components related to batch effects using the same criterion mentioned in section correcting for batch effects method “PLSDA-batch”.
# estimate the number of batch components
hfhs.batch.tune <- PLSDA_batch(X = hfhs.clr.less,
Y.trt = hfhs.trt.less,
Y.bat = hfhs.day.less,
ncomp.trt = 1,
keepX.trt = 2,
ncomp.bat = 10)
hfhs.batch.tune$explained_variance.bat #2## $X
## comp1 comp2 comp3 comp4 comp5 comp6 comp7
## 0.11496719 0.03611134 0.02995074 0.02497055 0.02954931 0.04284935 0.03468263
## comp8 comp9 comp10
## 0.02679416 0.02394709 0.02270728
##
## $Y
## comp1 comp2 comp3 comp4 comp5 comp6
## 0.493868226 0.506131774 0.511212568 0.484741160 0.004046272 0.512078352
## comp7 comp8 comp9 comp10
## 0.483749135 0.004172513 0.512156744 0.483406313sum(hfhs.batch.tune$explained_variance.bat$Y[1:2])## [1] 1According to the result, we need 2 batch related components to remove batch variance from the data with function PLSDA_batch().
##########
hfhs.sPLSDA_batch.res <- PLSDA_batch(X = hfhs.clr.less,
Y.trt = hfhs.trt.less,
Y.bat = hfhs.day.less,
ncomp.trt = 1,
keepX.trt = 2,
ncomp.bat = 2)
hfhs.sPLSDA_batch <- hfhs.sPLSDA_batch.res$X.nobatchPercentile Normalisation
To apply percentile_norm() function from PLSDAbatch package, we need to indicate a control group (ctrl.grp).
# HFHS data
hfhs.PN <- percentile_norm(data = hfhs.clr.less,
batch = hfhs.day.less,
trt = hfhs.trt.less,
ctrl.grp = 'Normal')RUVIII
The RUVIII() function is from ruv package. Similar to RUV4(), we use empirical negative control variables and getK() to determine the number of batch variables (k) to estimate. We also need sample replicates which should be structured into a mapping matrix using replicate.matrix(). We can then obtain batch effect corrected data applying RUVIII() with above elements.
hfhs.replicates <- hfhs.metadata.less$MouseID
hfhs.replicates.matrix <- replicate.matrix(hfhs.replicates)
hfhs.RUVIII <- RUVIII(Y = hfhs.clr.less,
M = hfhs.replicates.matrix,
ctl = hfhs.nc, k = hfhs.k)
rownames(hfhs.RUVIII) <- rownames(hfhs.clr.less)Compared to the AD data, the HFHS data have more appropriate sample replicates that fully capture the difference between different time points. The results of RUVIII applied to HFHS data would be better than AD data.
2.2.4 Assessing batch effect correction
We apply different visualisation and quantitative methods to assessing batch effect correction.
2.2.4.1 Methods that detect batch effects
PCA
In the HFHS data, we compare the PCA sample plots before and after batch effect correction with different methods.
hfhs.pca.before <- pca(hfhs.clr.less, ncomp = 3,
scale = TRUE)
hfhs.pca.rBE <- pca(hfhs.rBE, ncomp = 3,
scale = TRUE)
hfhs.pca.ComBat <- pca(hfhs.ComBat, ncomp = 3,
scale = TRUE)
hfhs.pca.PLSDA_batch <- pca(hfhs.PLSDA_batch, ncomp = 3,
scale = TRUE)
hfhs.pca.sPLSDA_batch <- pca(hfhs.sPLSDA_batch, ncomp = 3,
scale = TRUE)
hfhs.pca.PN <- pca(hfhs.PN, ncomp = 3,
scale = TRUE)
hfhs.pca.RUVIII <- pca(hfhs.RUVIII, ncomp = 3,
scale = TRUE)hfhs.pca.before.plot <-
Scatter_Density(object = hfhs.pca.before,
batch = hfhs.day.less,
trt = hfhs.trt.less,
title = 'Before')hfhs.pca.rBE.plot <-
Scatter_Density(object = hfhs.pca.rBE,
batch = hfhs.day.less,
trt = hfhs.trt.less,
title = 'removeBatchEffect')hfhs.pca.ComBat.plot <-
Scatter_Density(object = hfhs.pca.ComBat,
batch = hfhs.day.less,
trt = hfhs.trt.less,
title = 'ComBat')hfhs.pca.PLSDA_batch.plot <-
Scatter_Density(object = hfhs.pca.PLSDA_batch,
batch = hfhs.day.less,
trt = hfhs.trt.less,
title = 'PLSDA-batch')hfhs.pca.sPLSDA_batch.plot <-
Scatter_Density(object = hfhs.pca.sPLSDA_batch,
batch = hfhs.day.less,
trt = hfhs.trt.less,
title = 'sPLSDA-batch')hfhs.pca.PN.plot <-
Scatter_Density(object = hfhs.pca.PN,
batch = hfhs.day.less,
trt = hfhs.trt.less,
title = 'Percentile Normalisation')hfhs.pca.RUVIII.plot <-
Scatter_Density(object = hfhs.pca.RUVIII,
batch = hfhs.day.less,
trt = hfhs.trt.less,
title = 'RUVIII')
Figure 2.17: The PCA sample plots with densities before and after batch effect correction in the HFHS data.
In the above figures, the differences between the samples from different days were well removed after batch effect correction with PLSDA-batch and RUVIII. We can also compare the boxplots and density plots for key variables identified in PCA driving the major variance or in heatmaps showing obvious patterns before and after batch effect correction (results not shown).
pRDA
We calculate the global explained variance across all microbial variables using pRDA. To achieve this, we create a loop for each variable from the original (uncorrected) and batch effect-corrected data. The final results are then displayed with partVar_plot() from PLSDAbatch package.
# HFHS data
hfhs.corrected.list <- list(`Before correction` = hfhs.clr.less,
removeBatchEffect = hfhs.rBE,
ComBat = hfhs.ComBat,
`PLSDA-batch` = hfhs.PLSDA_batch,
`sPLSDA-batch` = hfhs.sPLSDA_batch,
`Percentile Normalisation` = hfhs.PN,
RUVIII = hfhs.RUVIII)
hfhs.prop.df <- data.frame(Treatment = NA, Batch = NA,
Intersection = NA,
Residuals = NA)
for(i in 1:length(hfhs.corrected.list)){
rda.res = varpart(hfhs.corrected.list[[i]], ~ trt, ~ day,
data = hfhs.factors.df, scale = T)
hfhs.prop.df[i, ] <- rda.res$part$indfract$Adj.R.squared}
rownames(hfhs.prop.df) = names(hfhs.corrected.list)
hfhs.prop.df <- hfhs.prop.df[, c(1,3,2,4)]
hfhs.prop.df[hfhs.prop.df < 0] = 0
hfhs.prop.df <- as.data.frame(t(apply(hfhs.prop.df, 1,
function(x){x/sum(x)})))
partVar_plot(prop.df = hfhs.prop.df)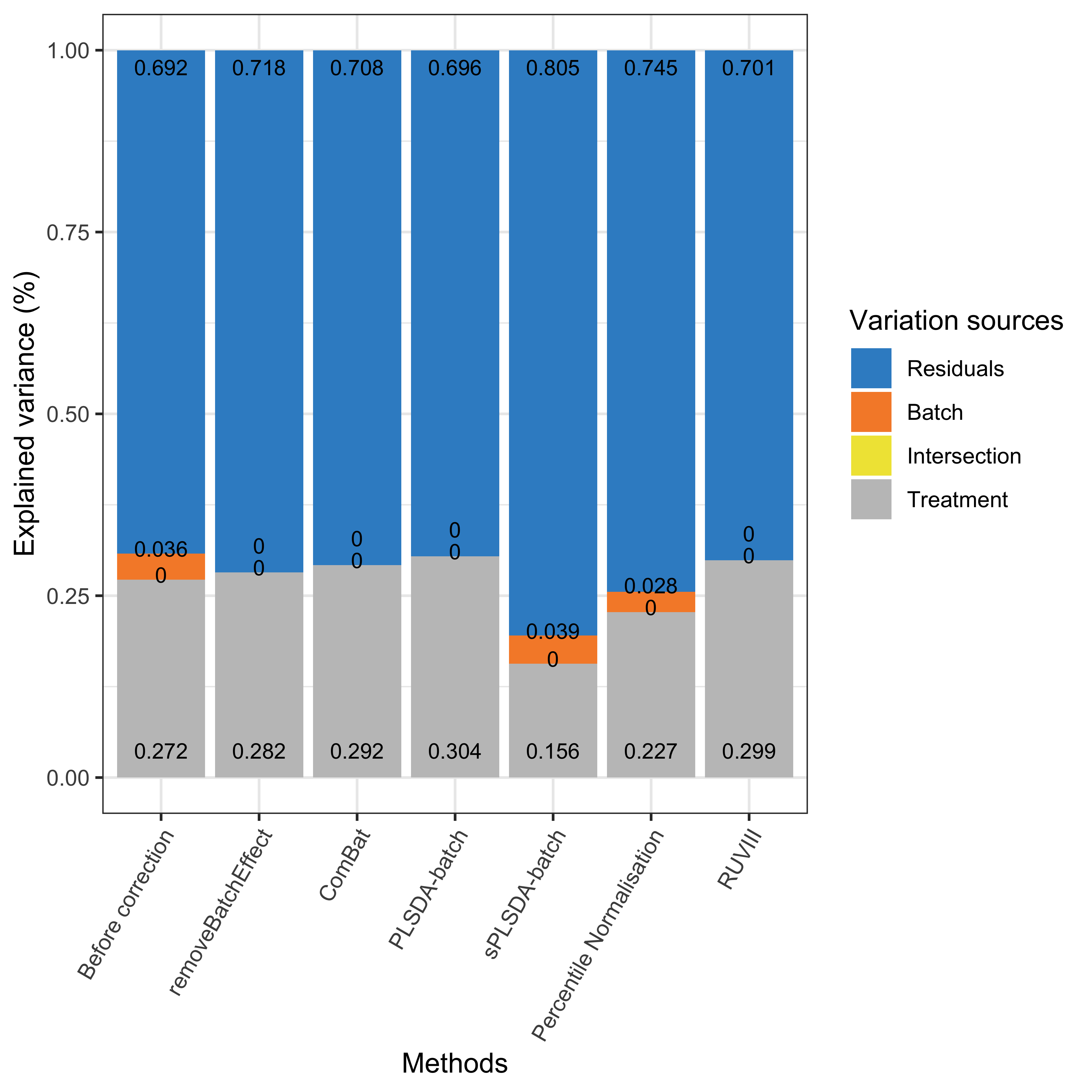
Figure 2.18: Global explained variance before and after batch effect correction for the HFHS data.
In the HFHS data, a small amount of batch variance was observed (3.6%) as shown in the above figure. PLSDA-batch achieved the best performance for preserving the largest treatment variance and completely removing batch variance compared to the other methods. The results also indicate that PLSDA-batch is more appropriate for weak batch effects, while sPLSDA-batch is more appropriate for strong batch effects. The RUVIII performed better in the HFHS data than the AD data because the sample replicates may help capturing more batch variation than in the AD data. Indeed, the sample replicates in HFHS data are across different day batches, while the replicates in AD data do not exist in all batches. Therefore, sample replicates play a critical role in RUVIII.
2.2.4.2 Other methods
\(R^2\)
The \(R^2\) values for each variable are calculated with lm() from stats package. To compare the \(R^2\) values among variables, we scale the corrected data before \(R^2\) calculation. The results are displayed with ggplot() from ggplot2 R package.
# scale
hfhs.corr_scale.list <- lapply(hfhs.corrected.list,
function(x){apply(x, 2, scale)})
# HFHS data
hfhs.r_values.list <- list()
for(i in 1:length(hfhs.corr_scale.list)){
hfhs.r_values <- data.frame(trt = NA, batch = NA)
for(c in 1:ncol(hfhs.corr_scale.list[[i]])){
hfhs.fit.res.trt <- lm(hfhs.corr_scale.list[[i]][,c] ~ hfhs.trt.less)
hfhs.r_values[c,1] <- summary(hfhs.fit.res.trt)$r.squared
hfhs.fit.res.batch <- lm(hfhs.corr_scale.list[[i]][,c] ~ hfhs.day.less)
hfhs.r_values[c,2] <- summary(hfhs.fit.res.batch)$r.squared
}
hfhs.r_values.list[[i]] <- hfhs.r_values
}
names(hfhs.r_values.list) <- names(hfhs.corr_scale.list)
hfhs.boxp.list <- list()
for(i in seq_len(length(hfhs.r_values.list))){
hfhs.boxp.list[[i]] <-
data.frame(r2 = c(hfhs.r_values.list[[i]][ ,'trt'],
hfhs.r_values.list[[i]][ ,'batch']),
Effects = as.factor(rep(c('Treatment','Batch'),
each = 515)))
}
names(hfhs.boxp.list) <- names(hfhs.r_values.list)
hfhs.r2.boxp <- rbind(hfhs.boxp.list$`Before correction`,
hfhs.boxp.list$removeBatchEffect,
hfhs.boxp.list$ComBat,
hfhs.boxp.list$`PLSDA-batch`,
hfhs.boxp.list$`sPLSDA-batch`,
hfhs.boxp.list$`Percentile Normalisation`,
hfhs.boxp.list$RUVIII)
hfhs.r2.boxp$methods <- rep(c('Before correction', ' removeBatchEffect',
'ComBat','PLSDA-batch', 'sPLSDA-batch',
'Percentile Normalisation', 'RUVIII'),
each = 1030)
hfhs.r2.boxp$methods <- factor(hfhs.r2.boxp$methods,
levels = unique(hfhs.r2.boxp$methods))
ggplot(hfhs.r2.boxp, aes(x = Effects, y = r2, fill = Effects)) +
geom_boxplot(alpha = 0.80) +
theme_bw() +
theme(text = element_text(size = 18),
axis.title.x = element_blank(),
axis.title.y = element_blank(),
axis.text.x = element_text(angle = 60, hjust = 1, size = 18),
axis.text.y = element_text(size = 18),
panel.grid.minor.x = element_blank(),
panel.grid.major.x = element_blank(),
legend.position = "right") + facet_grid( ~ methods) +
scale_fill_manual(values=pb_color(c(12,14))) 
Figure 2.19: HFHS study: \(R^2\) values for each microbial variable before and after batch effect correction.
We observed from these plots that the data corrected by sPLSDA-batch, percentile normalisation still included many variables with a large proportion of batch variance.
##################################
hfhs.barp.list <- list()
for(i in seq_len(length(hfhs.r_values.list))){
hfhs.barp.list[[i]] <-
data.frame(r2 = c(sum(hfhs.r_values.list[[i]][ ,'trt']),
sum(hfhs.r_values.list[[i]][ ,'batch'])),
Effects = c('Treatment','Batch'))
}
names(hfhs.barp.list) <- names(hfhs.r_values.list)
hfhs.r2.barp <- rbind(hfhs.barp.list$`Before correction`,
hfhs.barp.list$removeBatchEffect,
hfhs.barp.list$ComBat,
hfhs.barp.list$`PLSDA-batch`,
hfhs.barp.list$`sPLSDA-batch`,
hfhs.barp.list$`Percentile Normalisation`,
hfhs.barp.list$RUVIII)
hfhs.r2.barp$methods <- rep(c('Before correction', ' removeBatchEffect',
'ComBat','PLSDA-batch', 'sPLSDA-batch',
'Percentile Normalisation', 'RUVIII'), each = 2)
hfhs.r2.barp$methods <- factor(hfhs.r2.barp$methods,
levels = unique(hfhs.r2.barp$methods))
ggplot(hfhs.r2.barp, aes(x = Effects, y = r2, fill = Effects)) +
geom_bar(stat="identity") +
theme_bw() +
theme(text = element_text(size = 18),
axis.title.x = element_blank(),
axis.title.y = element_blank(),
axis.text.x = element_text(angle = 60, hjust = 1, size = 18),
axis.text.y = element_text(size = 18),
panel.grid.minor.x = element_blank(),
panel.grid.major.x = element_blank(),
legend.position = "right") + facet_grid( ~ methods) +
scale_fill_manual(values=pb_color(c(12,14)))
Figure 2.20: HFHS study: the sum of \(R^2\) values for each microbial variable before and after batch effect correction.
When considering the sum of all variables, the remaining batch variance of corrected data from PLSDA-batch is greater than removeBatchEffect, ComBat and RUVIII. The preserved treatment variance of corrected data from PLSDA-batch is the largest.
Alignment scores
We use the alignment_score() function from PLSDAbatch. We need to specify the proportion of data variance to explain (var), the number of nearest neighbours (k) and the number of principal components to estimate (ncomp). We then use ggplot() function from ggplot2 to visualise the results.
# HFHS data
hfhs.var = 0.95
hfhs.k = 15
hfhs.scores <- c()
for(i in 1:length(hfhs.corrected.list)){
res <- alignment_score(data = hfhs.corrected.list[[i]],
batch = hfhs.day.less,
var = hfhs.var,
k = hfhs.k,
ncomp = 130)
hfhs.scores <- c(hfhs.scores, res)
}
hfhs.scores.df <- data.frame(scores = hfhs.scores,
methods = names(hfhs.corrected.list))
hfhs.scores.df$methods <- factor(hfhs.scores.df$methods,
levels = rev(names(hfhs.corrected.list)))
ggplot() + geom_col(aes(x = hfhs.scores.df$methods,
y = hfhs.scores.df$scores)) +
geom_text(aes(x = hfhs.scores.df$methods,
y = hfhs.scores.df$scores/2,
label = round(hfhs.scores.df$scores, 3)),
size = 3, col = 'white') +
coord_flip() + theme_bw() + ylab('Alignment Scores') +
xlab('') + ylim(0,0.85)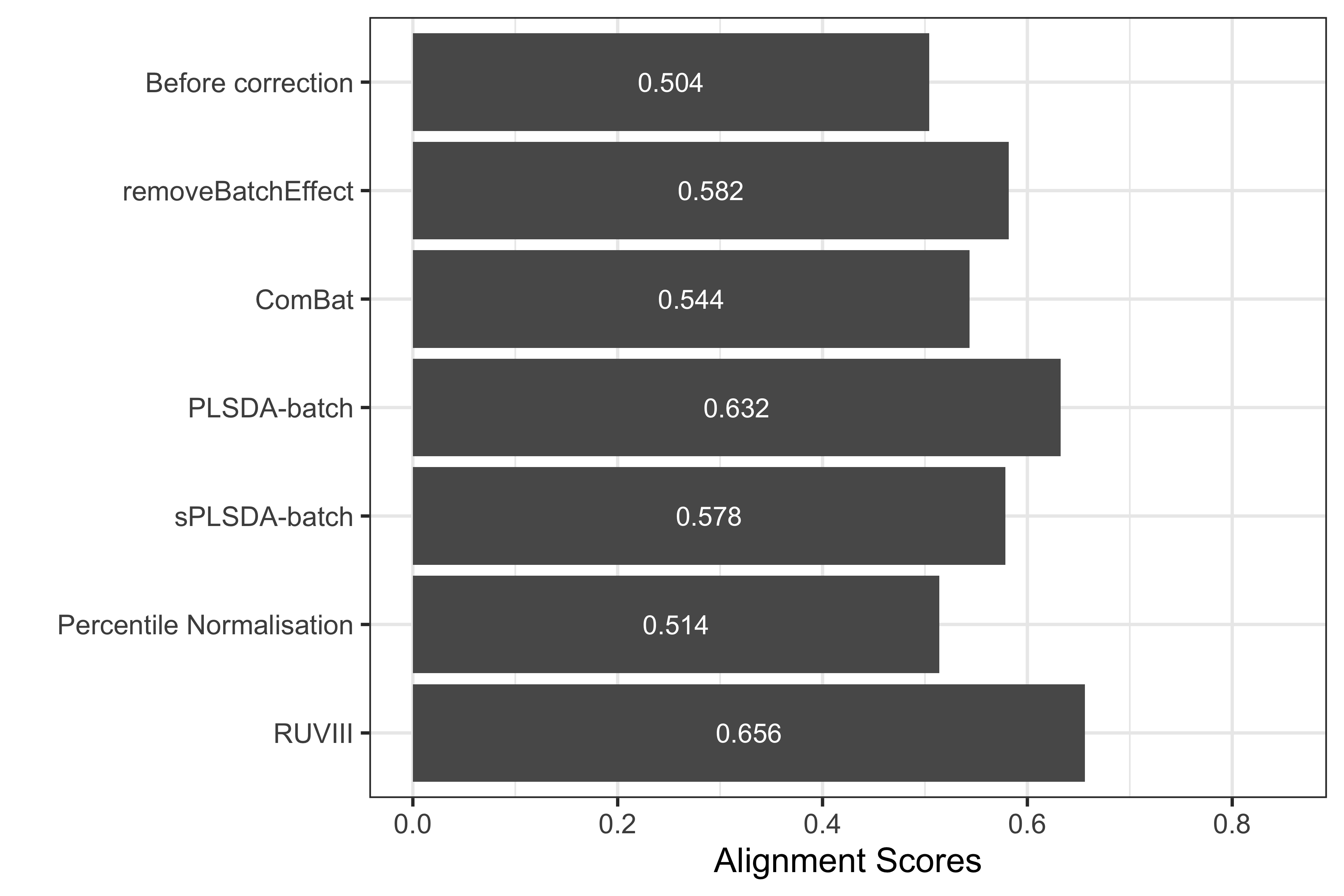
Figure 2.21: Comparison of alignment scores before and after batch effect correction using different methods for the HFHS data.
The alignment scores complement the PCA results, especially when batch effect removal is difficult to assess on PCA sample plots. For example in the PCA plots for the HFHS data, we observed that the samples across different batches were better mixed after batch effect correction with PLSDA-batch and RUVIII than before, while the performance of these two methods was difficult to compare. Since a higher alignment score indicates that samples are better mixed, as shown in the above figure, RUVIII gave a superior performance compared to the other methods.
We recommend the sparse version of PLSDA-batch for a very strong batch effect, for example, in the AD data. However, for a weak batch effect, we do not recommend removing batch effects in the HFHS data, but if we have to, we recommend using PLSDA-batch. It is easier to lose treatment variation when the batch variation is very small. Therefore PLSDA-batch can better ensure the complete preservation of treatment variation than a sparse version.
Variable selection
We use splsda() from mixOmics to select the top 50 microbial variables that, in combination, discriminate the different treatment groups in the HFHS data. We apply splsda() to the different batch effect corrected data from all methods. Then we use upset() from UpSetR package (Lex et al. 2014) to visualise the concordance of variables selected.
In the code below, we first need to convert the list of variables selected from different method-corrected data into a data frame compatible with upset() using fromList(). We then assign different colour schemes for each variable selection.
hfhs.splsda.select <- list()
for(i in 1:length(hfhs.corrected.list)){
splsda.res <- splsda(X = hfhs.corrected.list[[i]],
Y = hfhs.trt.less,
ncomp = 3, keepX = rep(50,3))
select.res <- selectVar(splsda.res, comp = 1)$name
hfhs.splsda.select[[i]] <- select.res
}
names(hfhs.splsda.select) <- names(hfhs.corrected.list)
# can only visualise 5 methods
hfhs.splsda.select <- hfhs.splsda.select[c(1:4,7)]
hfhs.splsda.upsetR <- fromList(hfhs.splsda.select)
upset(hfhs.splsda.upsetR, main.bar.color = 'gray36',
sets.bar.color = pb_color(c(25:22,20)), matrix.color = 'gray36',
order.by = 'freq', empty.intersections = 'on',
queries =
list(list(query = intersects, params = list('Before correction'),
color = pb_color(20), active = T),
list(query = intersects, params = list('removeBatchEffect'),
color = pb_color(22), active = T),
list(query = intersects, params = list('ComBat'),
color = pb_color(23), active = T),
list(query = intersects, params = list('PLSDA-batch'),
color = pb_color(24), active = T),
list(query = intersects, params = list('RUVIII'),
color = pb_color(25), active = T)))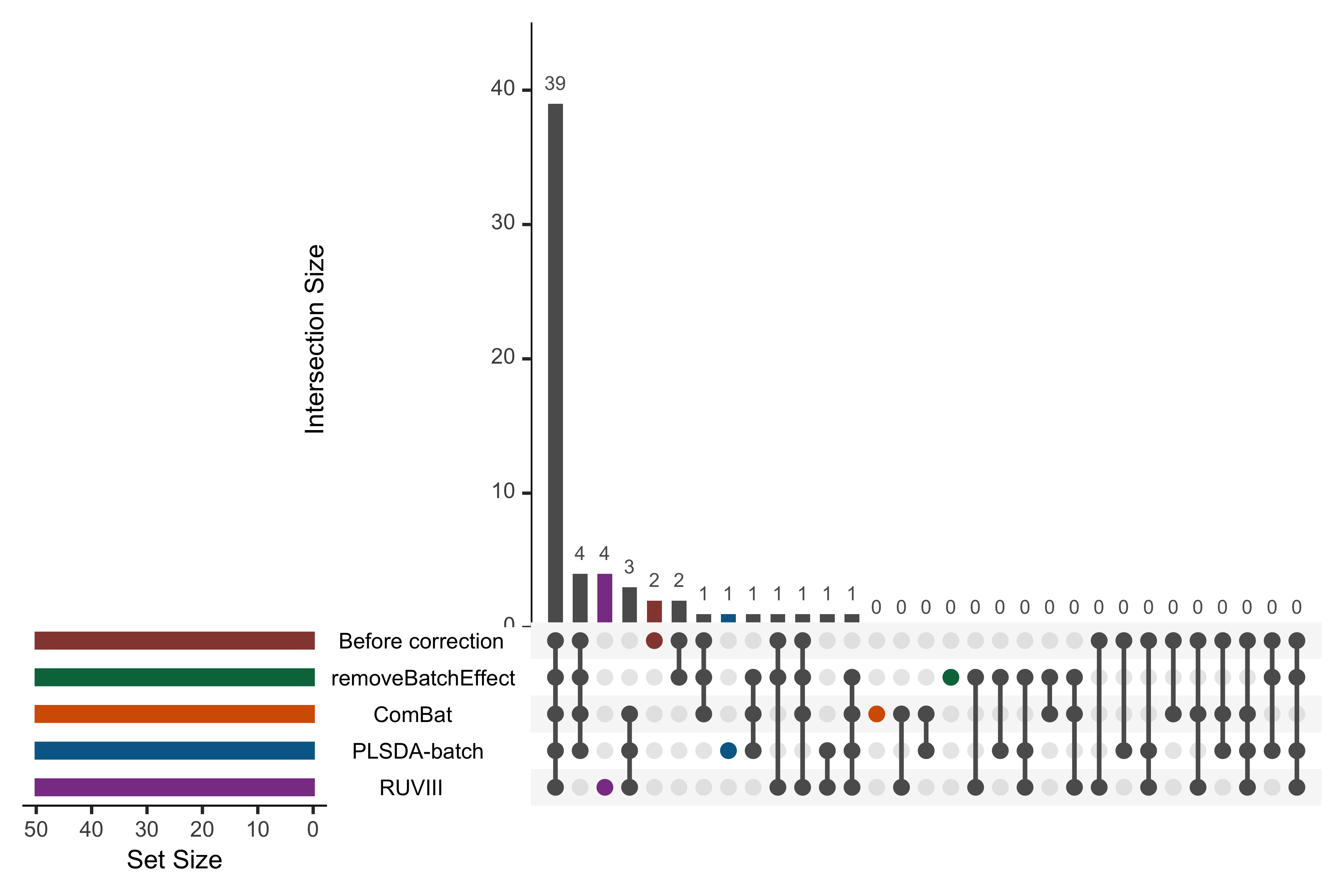
Figure 2.22: UpSet plot showing overlap between variables selected from different corrected data for the HFHS study.
In the above UpSet plot, the left bars indicate the number of variables selected from each data corrected with different methods. The right bar plot combined with the scatterplot show different intersection and their aggregates. We obtained an overlap of 39 out of 50 selected variables between different corrected and uncorrected data. However, the data from each method still included unique variables that were not selected in the other corrected data. As upset() can only include five datasets at once, we only display the uncorrected data and four corrected data that have been efficiently corrected for batch effects from our previous assessments.
hfhs.splsda.select.overlap <- venn(hfhs.splsda.select, show.plot = F)
hfhs.inters.splsda <- attr(hfhs.splsda.select.overlap, 'intersections')
hfhs.inters.splsda.taxa <-
lapply(hfhs.inters.splsda,
FUN = function(x){as.data.frame(HFHS_data$FullData$taxa[x, ])})
capture.output(hfhs.inters.splsda.taxa,
file = "GeneratedData/HFHSselected_50_splsda.txt")2.3 HD data
2.3.1 Data pre-processing
2.3.1.1 Prefiltering
We load the HD data stored internally with function data().
load(file = './data/HD_data.rda')
hd.count <- HD_data$FullData$X.count
dim(hd.count)## [1] 30 368hd.filter.res <- PreFL(data = hd.count)
hd.filter <- hd.filter.res$data.filter
dim(hd.filter)## [1] 30 269# zero proportion before filtering
hd.filter.res$zero.prob## [1] 0.4509058# zero proportion after filtering
sum(hd.filter == 0)/(nrow(hd.filter) * ncol(hd.filter))## [1] 0.3343247The raw HD data include 368 OTUs and 30 samples. We use the function PreFL() from our PLSDAbatch R package to filter the data. After filtering, the HD data were reduced to 269 OTUs and 30 samples. The proportion of zeroes was reduced from 45% to 33%.
2.3.2 Batch effect detection
2.3.2.1 PCA
We apply pca() function from mixOmics package to the HD data and use Scatter_Density() function from PLSDAbatch to represent the PCA sample plot with densities.
# HD data
hd.pca.before <- pca(hd.clr, ncomp = 3, scale = TRUE)
hd.metadata <- HD_data$FullData$metadata
hd.batch <- as.factor(hd.metadata$Cage)
hd.trt <- as.factor(hd.metadata$Genotype)
names(hd.batch) = names(hd.trt) = rownames(hd.metadata)
Scatter_Density(object = hd.pca.before,
batch = hd.batch,
trt = hd.trt,
title = 'HD data',
trt.legend.title = 'Genotype',
batch.legend.title = 'Cage', legend.cex = 0.6)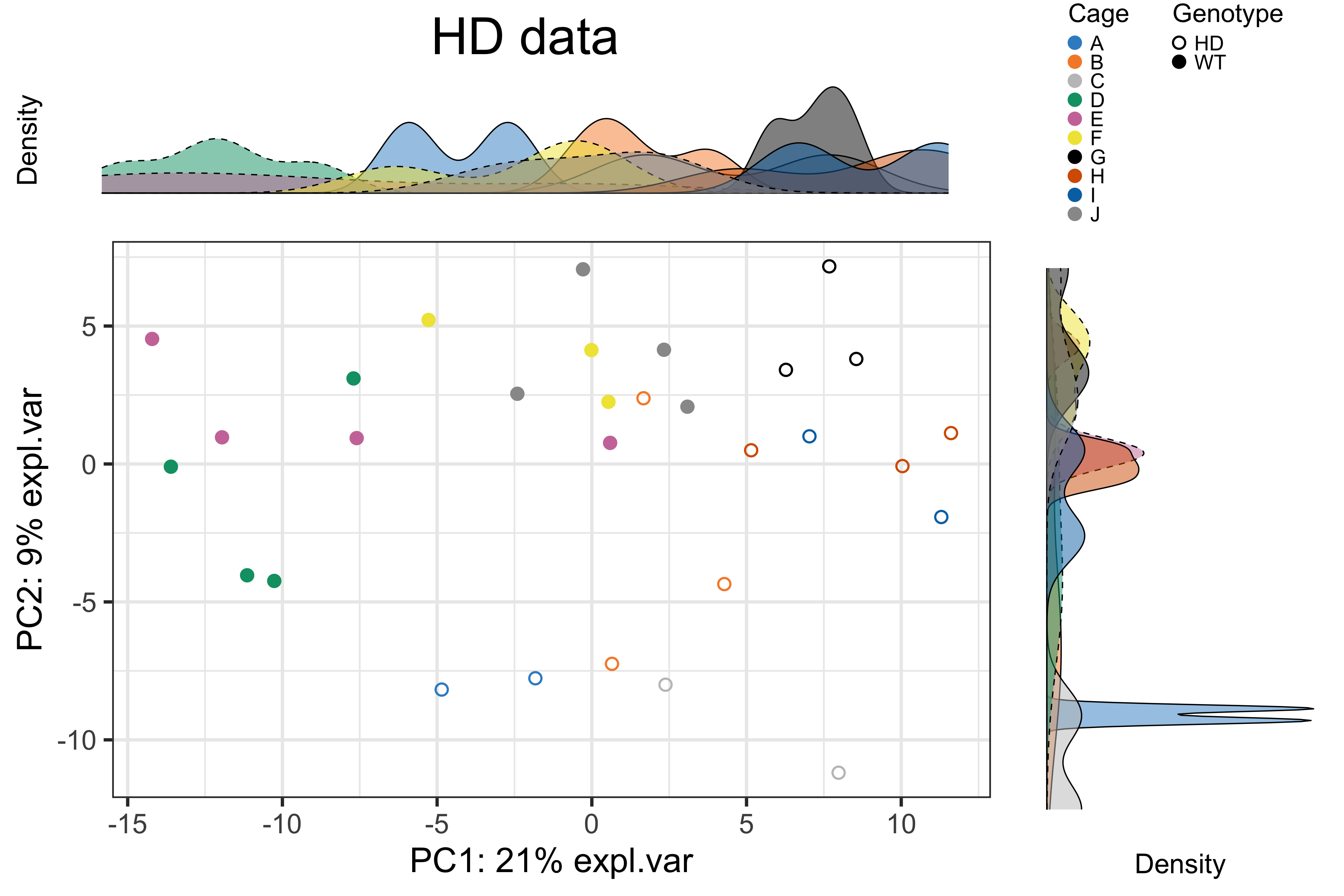
Figure 2.23: The PCA sample plot with densities in the HD data.
In the above figure, we observed a clear difference between genotypes but vague separation between cages on the PCA plot.
2.3.2.2 Heatmap
We produce a heatmap using pheatmap package. The data first need to be scaled on both OTUs and samples.
# scale the clr data on both OTUs and samples
hd.clr.s <- scale(hd.clr, center = T, scale = T)
hd.clr.ss <- scale(t(hd.clr.s), center = T, scale = T)
hd.anno_col <- data.frame(Cage = hd.batch, Genotype = hd.trt)
hd.anno_colors <- list(Cage = color.mixo(1:10),
Genotype = pb_color(1:2))
names(hd.anno_colors$Cage) = levels(hd.batch)
names(hd.anno_colors$Genotype) = levels(hd.trt)
pheatmap(hd.clr.ss,
cluster_rows = F,
fontsize_row = 4,
fontsize_col = 6,
fontsize = 8,
clustering_distance_rows = 'euclidean',
clustering_method = 'ward.D',
treeheight_row = 30,
annotation_col = hd.anno_col,
annotation_colors = hd.anno_colors,
border_color = 'NA',
main = 'HD data - Scaled')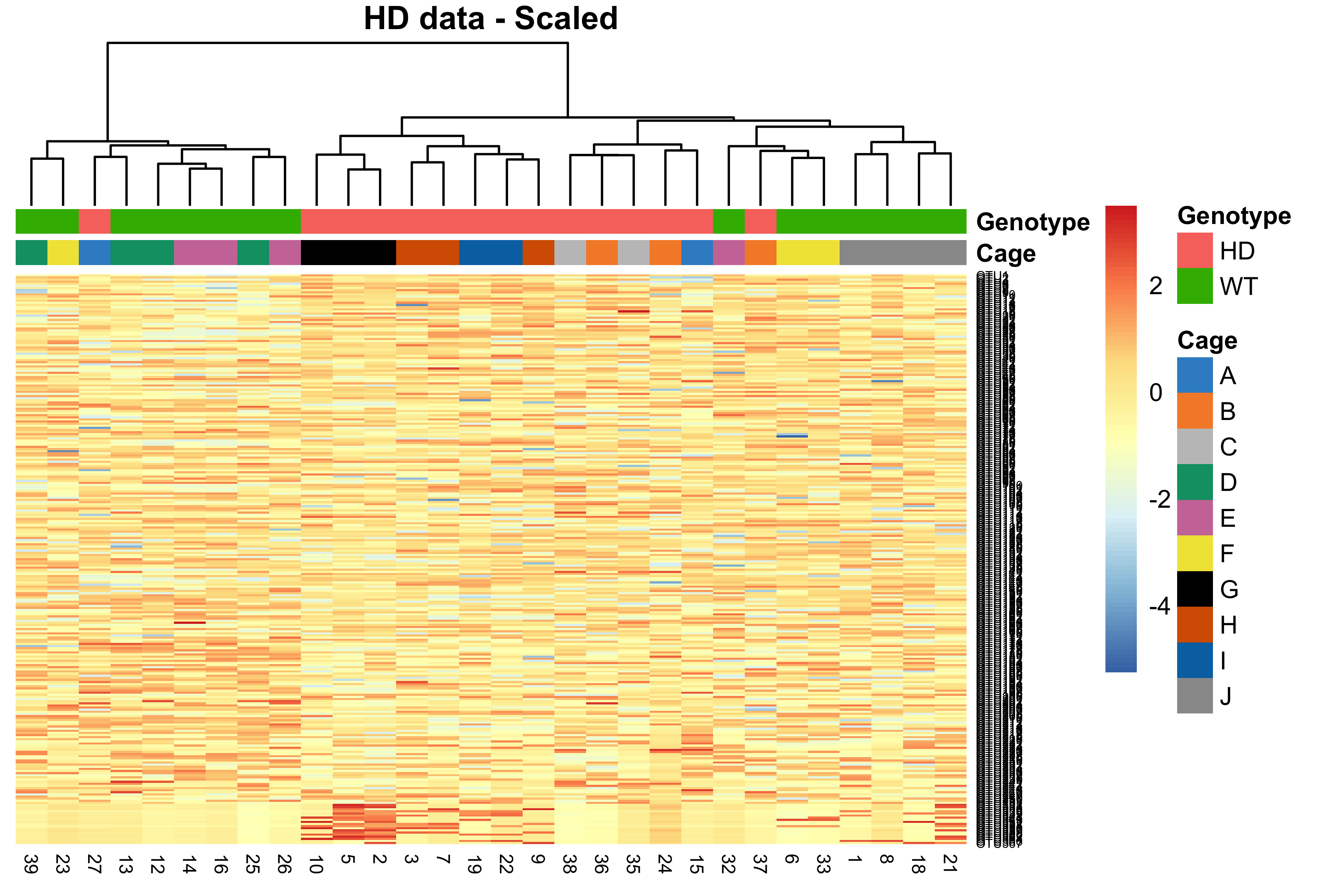
Figure 2.24: Hierarchical clustering for samples in the HD data.
In the heatmap, samples in the HD data were mostly grouped by genotypes instead of cages, indicating a weak cage effect.
2.3.2.3 pRDA
We apply pRDA with varpart() function from vegan R package.
hd.factors.df <- data.frame(trt = hd.trt, batch = hd.batch)
hd.rda.before <- varpart(hd.clr, ~ trt, ~ batch,
data = hd.factors.df, scale = T)
hd.rda.before$part$indfract## Df R.squared Adj.R.squared Testable
## [a] = X1|X2 0 NA 1.110223e-16 FALSE
## [b] = X2|X1 8 NA 1.608205e-01 TRUE
## [c] 0 NA 9.730583e-02 FALSE
## [d] = Residuals NA NA 7.418737e-01 FALSEIn the result, X1 and X2 represent the first and second covariates fitted in the model. [a], [b] represent the independent proportion of variance explained by X1 and X2 respectively, and [c] represents the intersection variance shared between X1 and X2. Collinearity was detected in the HD data between treatment and batch as indicated by lines [a] and [c] that all treatment variance ([a]: Adj.R.squared = 0, [c]: Adj.R.squared = 0.0973) was explained as intersection variance. The batch x treatment design in the HD data is nested, in such a design the intersection variance is usually considerable. As the intersection is shared between batch and treatment effects, the batch variance in the HD data is larger than the treatment variance.
2.3.3 Managing batch effects
Because of the nested batch x treatment design in the HD data, the only way to account for the batch effect (i.e., the cage effect) is to apply linear mixed model and include the batch effect as a random effect.
2.3.3.1 Accounting for batch effects
Linear regression
Linear regression is conducted with linear_regres() function in PLSDAbatch. We integrated the performance package that assesses performance of regression models into our function linear_regres(). Therefore, we can apply check_model() from performance to the outputs from linear_regres() to diagnose the validity of the model fitted with treatment and batch effects for each variable (LÃŒdecke et al. 2020). We can extract performance measurements such as adjusted R2, RMSE, RSE, AIC and BIC for the models fitted with and without batch effects, which are also the outputs of linear_regres().
We apply a linear mixed model and fit the batch effect as a random effect because the design of the HD data is nested. In such a design, the number of batches should be larger than treatment groups; otherwise, the linear mixed model cannot address the batch effect. Note: we assume that there is no interaction between batch and treatment effects on any microbial variable.
# HD data
hd.clr <- hd.clr[1:nrow(hd.clr), 1:ncol(hd.clr)]
hd.lmm <- linear_regres(data = hd.clr, trt = hd.trt,
batch.random = hd.batch,
type = 'linear mixed model')hd.p <- sapply(hd.lmm$lmm.table, function(x){x$coefficients[2,5]})
hd.p.adj <- p.adjust(p = hd.p, method = 'fdr')
check_model(hd.lmm$model$OTU1)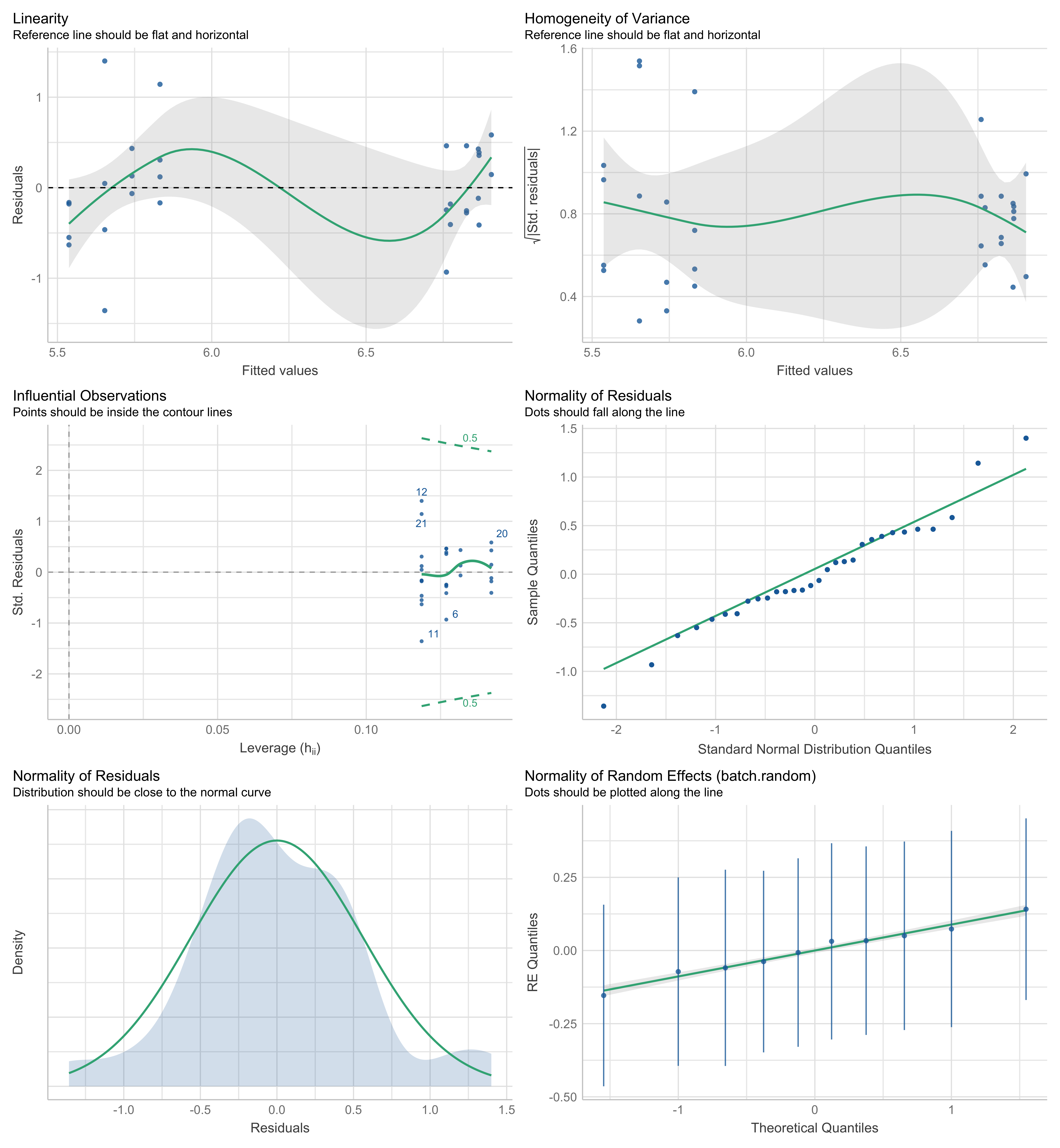
Figure 2.25: Diagnostic plots for the model fitted with the cage effect of “OTU1” in the HD data.
According to the diagnostic plots of “OTU1” as shown in the above figure panel, the simulated data under the fitted model were not very close to the real data (shown as green line), indicating an imperfect fitness (top panel). The linearity (or homoscedasticity) and homogeneity of variance were not satisfied. Some samples could be classified as outliers with a Cook’s distance larger than or equal to 0.5, for example, “12”, “21”, “20”, “11” and “6” (middle panel). The distribution of residuals was not normal, while the one of random effects was very close to normal (bottom panel).
We then look at the AIC of models fitted with or without batch effects.
head(hd.lmm$AIC)## trt.only trt.batch
## OTU1 60.00637 65.46410
## OTU2 130.14167 130.96344
## OTU3 71.76985 75.58915
## OTU4 134.59992 134.04812
## OTU5 150.25059 148.30644
## OTU6 99.92864 99.05391For some OTUs, the model fitted without batch effects is better with a lower AIC. For example, “OTU1” and “OTU3”. “OTU5” is more appropriate within a model with batch effects. The others are similar within either model.
Since we apply a "linear mixed model" to the HD data, this type of model can only output conditional \(R^2\) that includes the variance of both fixed and random effects (treatment, fixed and random batch effects) and marginal \(R^2\) that includes only the variance of fixed effects (treatment and fixed batch effects) (Nakagawa and Schielzeth 2013). The marginal \(R^2\)s of the models with and without the batch effect should be the same theoretically, as marginal \(R^2\) only includes fixed effects and the treatment effect is the only fixed effect here. In the actual calculation, the results of these two models were not the same due to different ways of model fitting.
head(hd.lmm$cond.R2)## trt.only trt.batch
## OTU1 0.47917775 0.5161317
## OTU2 0.39223824 0.4729848
## OTU3 0.02091376 0.2636432
## OTU4 0.37200835 0.5672392
## OTU5 0.07858373 0.2938212
## OTU6 0.41388250 0.6143134head(hd.lmm$marg.R2)## trt.only trt.batch
## OTU1 0.47917775 0.46735273
## OTU2 0.39223824 0.38459672
## OTU3 0.02091376 0.01489608
## OTU4 0.37200835 0.36122754
## OTU5 0.07858373 0.06052938
## OTU6 0.41388250 0.40749149We observed that some variables resulted in singular fits (error message: Can't compute random effect variances. Some variance components equal zero. Your model may suffer from singulariy.), which are expected to happen in linear mixed models when covariates are nested. We recommend noting the variables for which this error occurs, as it may lead to unreliable results.