Chapter 3 Batch Effects Management in Simulation Studies (Gaussian Distribution)

3.1 Introduction

We adapted the simulation strategy that is component-based and multivariate from (Singh et al. 2019). We assumed the input data after filtering follow a lognormal distribution inspired from (Weiss et al. 2017), thus after Centered Log Ratio (CLR) transformed follow a Gaussian distribution. Thus, we simulated components from a Gaussian distribution across all samples. The data matrix was generated based on the simulated components and corresponding loading vectors for each variable. Each simulated dataset included 300 variables and 40 samples grouped according to two treatments (trt1 and trt2) and two batches (batch1 and batch2). Different parameters including amount of batch and treatment variability among samples, number of variables with batch and/or treatment effects, balanced and unbalanced batch \(\times\) treatment designs were considered and summarised in the table below.

Table 1: Summary of simulation scenarios (Gaussian distribution). For a given choice of parameters reported in this table, each simulation was repeated 50 times. \(M^{(trt)}, M^{(batch)}\) and \(M^{(trt \ \& \ batch)}\) represent the number of variables with treatment, batch, or both effects respectively. Simu 6 includes parameters reflective of real data.

\(\mu_{(trt)}\) \(\sigma'_{(trt)}\) \(\mu_{(batch)}\) \(\sigma'_{(batch)}\) \(M^{(trt)}\) \(M^{(batch)}\) \(M^{(trt \ \& \ batch)}\)
Simu 1 3 1 7 {1,4,8} 60 150 0
Simu 2 {3,5,7} 1 7 8 60 150 0
Simu 3 3 {1,2,4} 7 8 60 150 0
Simu 4 3 2 7 8 {30,60,100,150} 150 0
Simu 5 3 2 7 8 60 {30,60,100,150} 0
Simu 6 3 2 7 8 60 150 {0,18,30,42,60}

We first generated two base components \(t^{(trt)}\) and \(t^{(batch)}\) to represent the underlying treatment and batch variation across samples in the datasets. The samples with trt1 or trt2 in the component \(t^{(trt)}\) were generated from \(N(-\mu_{(trt)}, \sigma^{'2}_{(trt)})\) and \(N(\mu_{(trt)}, \sigma^{'2}_{(trt)})\) respectively, where \(\sigma^{'2}_{(trt)}\) refers to the variability of treatment effect among samples, and similarly for the batch component. We then sampled the corresponding loading vectors \(\alpha^{(trt)}\) and \(\alpha^{(batch)}\) from a uniform distribution \([-0.3, -0.2]\cup [0.2,0.3]\) respectively and scaled them as an unit vector. We subsequently constructed the treatment relevant matrix as \(X^{(trt)} = t^{(trt)}(\alpha^{(trt)})^{\top}\) and similarly for the batch relevant matrix.

We also generated background noise \(E\) (\(E \in \mathbb{R}^{40 \times 300}\)), where each element was randomly sampled from \(N(0, 0.2^{2})\). The final simulated dataset \(X_{result}\) was constructed based on the treatment, batch relevant matrices and background noise. Starting with \(X_{result} = E\), we then added different types of variables, such that:

\[X_{result}[ ,\mbox{variables}^{(trt)}] = E[ ,\mbox{variables}^{(trt)}] + X^{(trt)}\] \[X_{result}[ ,\mbox{variables}^{(batch)}] = X_{result}[ ,\mbox{variables}^{(batch)}] + X^{(batch)},\]

where variables with treatment or batch effects were randomly indexed in the data.

In addition to the data with batch effects, we also simulated a ground-truth dataset that only included the background noise and treatment but no batch effect to evaluate batch effect corrected datasets.

In these simulation scenarios, for PLSDA-batch we set \(C-1\) (or \(B-1\)) components associated with treatment (or batch) effects (where \(C\) and \(B\) represent the total number of treatment and batch groups respectively) as \(C-1\) (\(B-1\)) components are likely to explain 100% variance in \(Y\). The number of variables with a true treatment effect (\(M^{(trt)}\)) is set as the optimal number to select on each treatment component in sPLSDA-batch.

To save space, here we only describe one scenario that we believe is a representative of real data (\(M^{(trt \ \& \ batch)} = 30\), simu 6 in Table 1).

3.2 Simulations

3.2.1 Balanced batch \(\times\) treatment design

The balanced batch \(\times\) treatment experimental design included 10 samples from two batches respectively in each treatment group (see Table 2)

Table 2: Balanced batch \(\times\) treatment design in the simulation study

Trt1 Trt2
Batch1 10 10
Batch2 10 10 
nitr <- 50
p_total <- 300
p_trt_relevant <- 60
p_bat_relevant <- 150

# global variance (RDA)
gvar.before <- gvar.clean <- gvar.rbe <- gvar.combat <- 
  gvar.plsdab <- gvar.splsdab <- data.frame(treatment = NA, batch = NA,  
                                            intersection = NA, 
                                            residual = NA)

# individual variance (R2)
r2.trt.before <- r2.trt.clean <- r2.trt.rbe  <- r2.trt.combat <- 
  r2.trt.plsdab <- r2.trt.splsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                       ncol = nitr))
r2.batch.before <- r2.batch.clean <- r2.batch.rbe  <- r2.batch.combat <- 
  r2.batch.plsdab <- r2.batch.splsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                           ncol = nitr))

# precision & recall & F1 (ANOVA)
precision_limma <- recall_limma <- F1_limma <- 
  data.frame(before = NA, clean = NA, rbe = NA, combat = NA, 
             plsda_batch = NA, splsda_batch = NA)

# precision & recall & F1 (sPLSDA)
precision_splsda <- recall_splsda <- F1_splsda <- 
  data.frame(before = NA, clean = NA, rbe = NA, combat = NA, 
             plsda_batch = NA, splsda_batch = NA)

for(i in seq_len(nitr)){
  ### initial setup ###
  simulation <- simData_Gaussian(mean.batch = 7, sd.batch = 8, 
                                 mean.trt = 3, sd.trt = 2, 
                                 N = 40, p_total = 300, 
                                 p_trt_relevant = 60, 
                                 p_bat_relevant = 150, 
                                 percentage_overlap_samples = 0.5,
                                 percentage_overlap_variables = 0.5, seeds = i)
  
  X <- simulation$data
  trt <- simulation$Y.trt
  batch <- simulation$Y.bat
  true.trt <- simulation$true.trt
  true.batch <- simulation$true.batch
  
  Batch_Trt.factors <- data.frame(Batch = batch, Treatment = trt)
  
  ### Before correction ###
  # global variance (RDA)
  rda.before = varpart(scale(X), ~ Treatment, ~ Batch, 
                       data = Batch_Trt.factors)
  gvar.before[i, ] <- rda.before$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.before <- c()
  indiv.batch.before <- c()
  for(c in seq_len(ncol(X))){
    fit.res1 <- lm(scale(X)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.before <- c(indiv.trt.before, fit.summary1$r.squared)
    indiv.batch.before <- c(indiv.batch.before, fit.summary2$r.squared)
  }
  r2.trt.before[ ,i] <-  indiv.trt.before
  r2.batch.before[ ,i] <-  indiv.batch.before
  
  # precision & recall & F1 (ANOVA)
  fit.before <- lmFit(t(scale(X)), design = model.matrix( ~ 0 + as.factor(trt)))
  fit.before <- contrasts.fit(fit.before, contrasts = c(1,-1))
  fit.result.before <- topTable(eBayes(fit.before), number = p_total)
  otu.sig.before <- rownames(fit.result.before)[fit.result.before$adj.P.Val <= 
                                                  0.05]
  
  precision_limma.before <- length(intersect(true.trt, otu.sig.before))/
    length(otu.sig.before)
  recall_limma.before <- length(intersect(true.trt, otu.sig.before))/
    length(true.trt)
  F1_limma.before <- (2*precision_limma.before*recall_limma.before)/
    (precision_limma.before + recall_limma.before)
  
  ## replace NA value with 0
  if(precision_limma.before == 'NaN'){
    precision_limma.before = 0
  }
  if(F1_limma.before == 'NaN'){
    F1_limma.before = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.before_splsda <- splsda(X = X, Y = trt, ncomp = 1, 
                              keepX = length(true.trt))
  otu.dcn.before <- which(fit.before_splsda$loadings$X[ ,1] != 0)
  
  precision_splsda.before <- length(intersect(true.trt, otu.dcn.before))/
    length(otu.dcn.before)
  recall_splsda.before <- length(intersect(true.trt, otu.dcn.before))/
    length(true.trt)
  F1_splsda.before <- (2*precision_splsda.before*recall_splsda.before)/
    (precision_splsda.before + recall_splsda.before)
  
  ## replace NA value with 0
  if(F1_splsda.before == 'NaN'){
    F1_splsda.before = 0
  }
  
  ##############################################################################
  ### Ground-truth data ###
  X.clean <- simulation$cleanData
  # global variance (RDA)
  rda.clean = varpart(scale(X.clean), ~ Treatment, ~ Batch, 
                      data = Batch_Trt.factors)
  gvar.clean[i, ] <- rda.clean$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.clean <- c()
  indiv.batch.clean <- c()
  for(c in seq_len(ncol(X.clean))){
    fit.res1 <- lm(scale(X.clean)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.clean)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.clean <- c(indiv.trt.clean, fit.summary1$r.squared)
    indiv.batch.clean <- c(indiv.batch.clean, fit.summary2$r.squared)
  }
  r2.trt.clean[ ,i] <-  indiv.trt.clean
  r2.batch.clean[ ,i] <-  indiv.batch.clean
  
  # precision & recall & F1 (ANOVA)
  fit.clean <- lmFit(t(scale(X.clean)), 
                     design = model.matrix( ~ 0 + as.factor(trt)))
  fit.clean <- contrasts.fit(fit.clean, contrasts = c(1,-1))
  fit.result.clean <- topTable(eBayes(fit.clean), number = p_total)
  otu.sig.clean <- rownames(fit.result.clean)[fit.result.clean$adj.P.Val <= 
                                                0.05]
  
  precision_limma.clean <- length(intersect(true.trt, otu.sig.clean))/
    length(otu.sig.clean)
  recall_limma.clean <- length(intersect(true.trt, otu.sig.clean))/
    length(true.trt)
  F1_limma.clean <- (2*precision_limma.clean*recall_limma.clean)/
    (precision_limma.clean + recall_limma.clean)
  
  ## replace NA value with 0
  if(precision_limma.clean == 'NaN'){
    precision_limma.clean = 0
  }
  if(F1_limma.clean == 'NaN'){
    F1_limma.clean = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.clean_splsda <- splsda(X = X.clean, Y = trt, ncomp = 1, 
                             keepX = length(true.trt))
  otu.dcn.clean <- which(fit.clean_splsda$loadings$X[ ,1] != 0)
  
  precision_splsda.clean <- length(intersect(true.trt, otu.dcn.clean))/
    length(otu.dcn.clean)
  recall_splsda.clean <- length(intersect(true.trt, otu.dcn.clean))/
    length(true.trt)
  F1_splsda.clean <- (2*precision_splsda.clean*recall_splsda.clean)/
    (precision_splsda.clean + recall_splsda.clean)
  
  ## replace NA value with 0
  if(F1_splsda.clean == 'NaN'){
    F1_splsda.clean = 0
  }
  
  ##############################################################################
  ### removeBatchEffect corrected data ###
  X.rbe <-t(removeBatchEffect(t(X), batch = batch, 
                              design = model.matrix( ~ 0 + as.factor(trt))))
  
  # global variance (RDA)
  rda.rbe = varpart(scale(X.rbe), ~ Treatment, ~ Batch, 
                    data = Batch_Trt.factors)
  gvar.rbe[i, ] <- rda.rbe$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.rbe <- c()
  indiv.batch.rbe <- c()
  for(c in seq_len(ncol(X.rbe))){
    fit.res1 <- lm(scale(X.rbe)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.rbe)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.rbe <- c(indiv.trt.rbe, fit.summary1$r.squared)
    indiv.batch.rbe <- c(indiv.batch.rbe, fit.summary2$r.squared)
  }
  r2.trt.rbe[ ,i] <-  indiv.trt.rbe
  r2.batch.rbe[ ,i] <-  indiv.batch.rbe
  
  # precision & recall & F1 (ANOVA)
  fit.rbe <- lmFit(t(scale(X.rbe)), 
                   design = model.matrix( ~ 0 + as.factor(trt)))
  fit.rbe <- contrasts.fit(fit.rbe, contrasts = c(1,-1))
  fit.result.rbe <- topTable(eBayes(fit.rbe), number = p_total)
  otu.sig.rbe <- rownames(fit.result.rbe)[fit.result.rbe$adj.P.Val <= 0.05]
  
  precision_limma.rbe <- length(intersect(true.trt, otu.sig.rbe))/
    length(otu.sig.rbe)
  recall_limma.rbe <- length(intersect(true.trt, otu.sig.rbe))/
    length(true.trt)
  F1_limma.rbe <- (2*precision_limma.rbe*recall_limma.rbe)/
    (precision_limma.rbe + recall_limma.rbe)
  
  ## replace NA value with 0
  if(precision_limma.rbe == 'NaN'){
    precision_limma.rbe = 0
  }
  if(F1_limma.rbe == 'NaN'){
    F1_limma.rbe = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.rbe_splsda <- splsda(X = X.rbe, Y = trt, ncomp = 1, 
                           keepX = length(true.trt))
  otu.dcn.rbe <- which(fit.rbe_splsda$loadings$X[ ,1] != 0)
  
  precision_splsda.rbe <- length(intersect(true.trt, otu.dcn.rbe))/
    length(otu.dcn.rbe)
  recall_splsda.rbe <- length(intersect(true.trt, otu.dcn.rbe))/
    length(true.trt)
  F1_splsda.rbe <- (2*precision_splsda.rbe*recall_splsda.rbe)/
    (precision_splsda.rbe + recall_splsda.rbe)
  
  ## replace NA value with 0
  if(F1_splsda.rbe == 'NaN'){
    F1_splsda.rbe = 0
  }
  
  ##############################################################################
  ### ComBat corrected data ###
  X.combat <- t(ComBat(dat = t(X), batch = batch, 
                       mod = model.matrix( ~ as.factor(trt))))
  
  # global variance (RDA)
  rda.combat = varpart(scale(X.combat), ~ Treatment, ~ Batch, 
                       data = Batch_Trt.factors)
  gvar.combat[i, ] <- rda.combat$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.combat <- c()
  indiv.batch.combat <- c()
  for(c in seq_len(ncol(X.combat))){
    fit.res1 <- lm(scale(X.combat)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.combat)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.combat <- c(indiv.trt.combat, fit.summary1$r.squared)
    indiv.batch.combat <- c(indiv.batch.combat, fit.summary2$r.squared)
  }
  r2.trt.combat[ ,i] <-  indiv.trt.combat
  r2.batch.combat[ ,i] <-  indiv.batch.combat
  
  # precision & recall & F1 (ANOVA)
  fit.combat <- lmFit(t(scale(X.combat)), 
                      design = model.matrix( ~ 0 + as.factor(trt)))
  fit.combat <- contrasts.fit(fit.combat, contrasts = c(1,-1))
  fit.result.combat <- topTable(eBayes(fit.combat), number = p_total)
  otu.sig.combat <- rownames(fit.result.combat)[fit.result.combat$adj.P.Val <= 
                                                  0.05]
  
  precision_limma.combat <- length(intersect(true.trt, otu.sig.combat))/
    length(otu.sig.combat)
  recall_limma.combat <- length(intersect(true.trt, otu.sig.combat))/
    length(true.trt)
  F1_limma.combat <- (2*precision_limma.combat*recall_limma.combat)/
    (precision_limma.combat + recall_limma.combat)
  
  ## replace NA value with 0
  if(precision_limma.combat == 'NaN'){
    precision_limma.combat = 0
  }
  if(F1_limma.combat == 'NaN'){
    F1_limma.combat = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.combat_splsda <- splsda(X = X.combat, Y = trt, ncomp = 1, 
                              keepX = length(true.trt))
  otu.dcn.combat <- which(fit.combat_splsda$loadings$X[ ,1] != 0)
  
  precision_splsda.combat <- length(intersect(true.trt, otu.dcn.combat))/
    length(otu.dcn.combat)
  recall_splsda.combat <- length(intersect(true.trt, otu.dcn.combat))/
    length(true.trt)
  F1_splsda.combat <- (2*precision_splsda.combat*recall_splsda.combat)/
    (precision_splsda.combat + recall_splsda.combat)
  
  ## replace NA value with 0
  if(F1_splsda.combat == 'NaN'){
    F1_splsda.combat = 0
  }
  
  ##############################################################################
  ### PLSDA-batch corrected data ###
  X.plsda_batch.correct <- PLSDA_batch(X = X, 
                                       Y.trt = trt, Y.bat = batch, 
                                       ncomp.trt = 1, ncomp.bat = 1)
  X.plsda_batch <- X.plsda_batch.correct$X.nobatch
  colnames(X.plsda_batch) <- seq_len(p_total)
  
  # global variance (RDA)
  rda.plsda_batch = varpart(scale(X.plsda_batch), ~ Treatment, ~ Batch, 
                            data = Batch_Trt.factors)
  gvar.plsdab[i, ] <- rda.plsda_batch$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.plsda_batch <- c()
  indiv.batch.plsda_batch <- c()
  for(c in seq_len(ncol(X.plsda_batch))){
    fit.res1 <- lm(scale(X.plsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.plsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.plsda_batch <- c(indiv.trt.plsda_batch, 
                               fit.summary1$r.squared)
    indiv.batch.plsda_batch <- c(indiv.batch.plsda_batch, 
                                 fit.summary2$r.squared)
  }
  r2.trt.plsdab[ ,i] <-  indiv.trt.plsda_batch
  r2.batch.plsdab[ ,i] <-  indiv.batch.plsda_batch
  
  # precision & recall & F1 (ANOVA)
  fit.plsda_batch <- lmFit(t(scale(X.plsda_batch)), 
                           design = model.matrix( ~ 0 + as.factor(trt)))
  fit.plsda_batch <- contrasts.fit(fit.plsda_batch, contrasts = c(1,-1))
  fit.result.plsda_batch <- topTable(eBayes(fit.plsda_batch), number = p_total)
  otu.sig.plsda_batch <- rownames(fit.result.plsda_batch)[
    fit.result.plsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.plsda_batch <- 
    length(intersect(true.trt, otu.sig.plsda_batch))/length(otu.sig.plsda_batch)
  recall_limma.plsda_batch <- 
    length(intersect(true.trt, otu.sig.plsda_batch))/length(true.trt)
  F1_limma.plsda_batch <- 
    (2*precision_limma.plsda_batch*recall_limma.plsda_batch)/
    (precision_limma.plsda_batch + recall_limma.plsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.plsda_batch == 'NaN'){
    precision_limma.plsda_batch = 0
  }
  if(F1_limma.plsda_batch == 'NaN'){
    F1_limma.plsda_batch = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.plsda_batch_splsda <- splsda(X = X.plsda_batch, Y = trt, ncomp = 1, 
                                   keepX = length(true.trt))
  otu.dcn.plsda_batch <- which(fit.plsda_batch_splsda$loadings$X[ ,1] != 0)
  
  precision_splsda.plsda_batch <- 
    length(intersect(true.trt, otu.dcn.plsda_batch))/length(otu.dcn.plsda_batch)
  recall_splsda.plsda_batch <- 
    length(intersect(true.trt, otu.dcn.plsda_batch))/length(true.trt)
  F1_splsda.plsda_batch <- 
    (2*precision_splsda.plsda_batch*recall_splsda.plsda_batch)/
    (precision_splsda.plsda_batch + recall_splsda.plsda_batch)
  
  ## replace NA value with 0
  if(F1_splsda.plsda_batch == 'NaN'){
    F1_splsda.plsda_batch = 0
  }
  
  ##############################################################################
  ### sPLSDA-batch corrected data ###
  X.splsda_batch.correct <- PLSDA_batch(X = X, 
                                        Y.trt = trt, 
                                        Y.bat = batch, 
                                        ncomp.trt = 1, 
                                        keepX.trt = length(true.trt), 
                                        ncomp.bat = 1)
  X.splsda_batch <- X.splsda_batch.correct$X.nobatch
  colnames(X.splsda_batch) <- seq_len(p_total)
  
  # global variance (RDA)
  rda.splsda_batch = varpart(scale(X.splsda_batch), ~ Treatment, ~ Batch, 
                             data = Batch_Trt.factors)
  gvar.splsdab[i, ] <- rda.splsda_batch$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.splsda_batch <- c()
  indiv.batch.splsda_batch <- c()
  for(c in seq_len(ncol(X.splsda_batch))){
    fit.res1 <- lm(scale(X.splsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.splsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.splsda_batch <- c(indiv.trt.splsda_batch, 
                                fit.summary1$r.squared)
    indiv.batch.splsda_batch <- c(indiv.batch.splsda_batch, 
                                  fit.summary2$r.squared)
  }
  r2.trt.splsdab[ ,i] <-  indiv.trt.splsda_batch
  r2.batch.splsdab[ ,i] <-  indiv.batch.splsda_batch
  
  # precision & recall & F1 (ANOVA)
  fit.splsda_batch <- lmFit(t(scale(X.splsda_batch)), 
                            design = model.matrix( ~ 0 + as.factor(trt)))
  fit.splsda_batch <- contrasts.fit(fit.splsda_batch, contrasts = c(1,-1))
  fit.result.splsda_batch <- topTable(eBayes(fit.splsda_batch), 
                                      number = p_total)
  otu.sig.splsda_batch <- rownames(fit.result.splsda_batch)[
    fit.result.splsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.splsda_batch <- 
    length(intersect(true.trt, otu.sig.splsda_batch))/
    length(otu.sig.splsda_batch)
  recall_limma.splsda_batch <- 
    length(intersect(true.trt, otu.sig.splsda_batch))/length(true.trt)
  F1_limma.splsda_batch <- 
    (2*precision_limma.splsda_batch*recall_limma.splsda_batch)/
    (precision_limma.splsda_batch + recall_limma.splsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.splsda_batch == 'NaN'){
    precision_limma.splsda_batch = 0
  }
  if(F1_limma.splsda_batch == 'NaN'){
    F1_limma.splsda_batch = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.splsda_batch_splsda <- splsda(X = X.splsda_batch, Y = trt, ncomp = 1, 
                                    keepX = length(true.trt))
  otu.dcn.splsda_batch <- which(fit.splsda_batch_splsda$loadings$X[ ,1] != 0)
  
  precision_splsda.splsda_batch <- 
    length(intersect(true.trt, otu.dcn.splsda_batch))/
    length(otu.dcn.splsda_batch)
  recall_splsda.splsda_batch <- 
    length(intersect(true.trt, otu.dcn.splsda_batch))/length(true.trt)
  F1_splsda.splsda_batch <- 
    (2*precision_splsda.splsda_batch*recall_splsda.splsda_batch)/
    (precision_splsda.splsda_batch + recall_splsda.splsda_batch)
  
  ## replace NA value with 0
  if(F1_splsda.splsda_batch == 'NaN'){
    F1_splsda.splsda_batch = 0
  }
  
  # summary
  # precision & recall & F1 (ANOVA)
  precision_limma[i, ] <- c(`Before correction` = precision_limma.before, 
                            `Ground-truth data` = precision_limma.clean,
                            `removeBatchEffect` = precision_limma.rbe,
                            ComBat = precision_limma.combat,
                            `PLSDA-batch` = precision_limma.plsda_batch,
                            `sPLSDA-batch` = precision_limma.splsda_batch)
  
  recall_limma[i, ] <- c(`Before correction` = recall_limma.before, 
                         `Ground-truth data` = recall_limma.clean,
                         `removeBatchEffect` = recall_limma.rbe,
                         ComBat = recall_limma.combat,
                         `PLSDA-batch` = recall_limma.plsda_batch,
                         `sPLSDA-batch` = recall_limma.splsda_batch)
  
  F1_limma[i, ] <- c(`Before correction` = F1_limma.before, 
                     `Ground-truth data` = F1_limma.clean,
                     `removeBatchEffect` = F1_limma.rbe,
                     ComBat = F1_limma.combat,
                     `PLSDA-batch` = F1_limma.plsda_batch,
                     `sPLSDA-batch` = F1_limma.splsda_batch)
  
  
  # precision & recall & F1 (sPLSDA)
  precision_splsda[i, ] <- c(`Before correction` = precision_splsda.before, 
                             `Ground-truth data` = precision_splsda.clean,
                             `removeBatchEffect` = precision_splsda.rbe,
                             ComBat = precision_splsda.combat,
                             `PLSDA-batch` = precision_splsda.plsda_batch,
                             `sPLSDA-batch` = precision_splsda.splsda_batch)
  
  recall_splsda[i, ] <- c(`Before correction` = recall_splsda.before, 
                          `Ground-truth data` = recall_splsda.clean,
                          `removeBatchEffect` = recall_splsda.rbe,
                          ComBat = recall_splsda.combat,
                          `PLSDA-batch` = recall_splsda.plsda_batch,
                          `sPLSDA-batch` = recall_splsda.splsda_batch)
  
  F1_splsda[i, ] <- c(`Before correction` = F1_splsda.before, 
                      `Ground-truth data` = F1_splsda.clean,
                      `removeBatchEffect` = F1_splsda.rbe,
                      ComBat = F1_splsda.combat,
                      `PLSDA-batch` = F1_splsda.plsda_batch,
                      `sPLSDA-batch` = F1_splsda.splsda_batch)
  
}

As the simulation step takes time, so we use the saved data into visulisation.

3.2.2 Figures

# global variance (RDA)
prop.gvar.all <- rbind(`Before correction` = colMeans(gvar.before),
                       `Ground-truth data` = colMeans(gvar.clean),
                       removeBatchEffect = colMeans(gvar.rbe),
                       ComBat = colMeans(gvar.combat),
                       `PLSDA-batch` = colMeans(gvar.plsdab),
                       `sPLSDA-batch` = colMeans(gvar.splsdab))

prop.gvar.all[prop.gvar.all < 0] = 0
prop.gvar.all <- t(apply(prop.gvar.all, 1, function(x){x/sum(x)}))
colnames(prop.gvar.all) <- c('Treatment', 'Intersection', 'Batch', 'Residuals')

partVar_plot(prop.df = prop.gvar.all)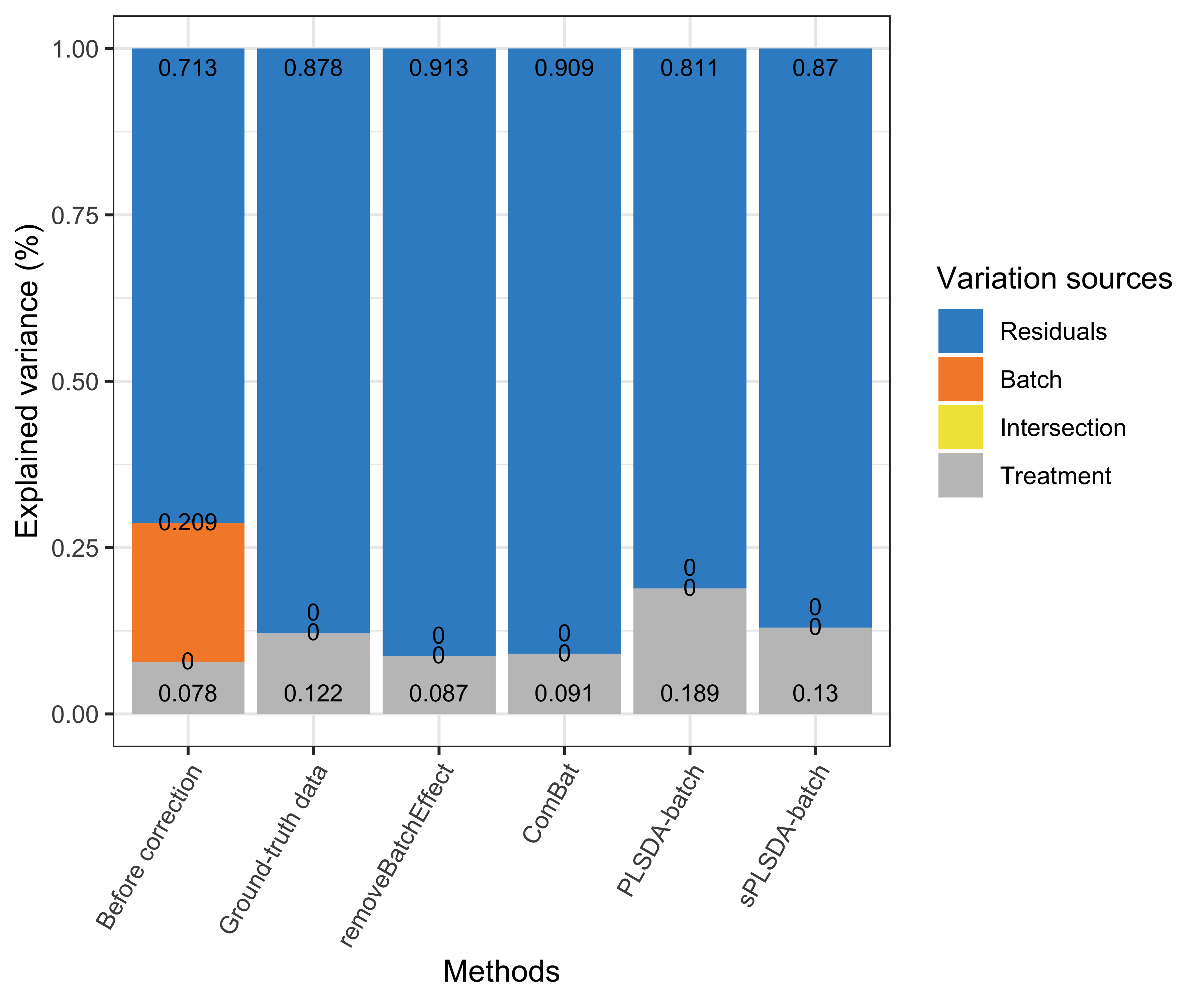
Figure 1: Simulation studies (Gaussian distribution): comparison of explained variance before and after batch effect correction for the balanced batch × treatment design.

Figure 3.1: Figure 1: Simulation studies (Gaussian distribution): comparison of explained variance before and after batch effect correction for the balanced batch × treatment design.

We first considered the proportion of variance explained by treatment and batch effects before and after batch effect correction across all variables using pRDA. Efficient batch effect correction methods should generate data with a smaller proportion of batch associated variance and larger proportion of treatment variance compared to the original data. The figure shows that there was no intersection shared between treatment and batch variation with a balanced batch \(\times\) treatment design. All methods successfully removed batch variation, but PLSDA-batch and sPLSDA-batch preserved more proportion of treatment variance than removeBatchEffect and ComBat. In addition, the data corrected by sPLSDA-batch included almost as much proportion of treatment variance as the ground-truth data.

################################################################################
# individual variance (R2)
# color
gcolor <- c(rep(pb_color(16), p_trt_relevant), 
            rep(pb_color(17), (p_total - p_trt_relevant)))
gcolor[intersect(true.trt, true.batch)] = pb_color(18)
gcolor[setdiff(seq_len(p_total), union(true.trt, true.batch))] = pb_color(15)

xlabs = 'R2(variable, treatment)'
ylabs = 'R2(variable, batch)'
edgex = 0.7
edgey = 0.5

# scatterplot
par(mfrow = c(3,2))
plot(rowMeans(r2.trt.before), rowMeans(r2.batch.before), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), 
     main = 'Before correction', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)

plot(rowMeans(r2.trt.clean), rowMeans(r2.batch.clean), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), 
     main = 'Ground-truth data', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)

plot(rowMeans(r2.trt.rbe), rowMeans(r2.batch.rbe), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), 
     main = 'removeBatchEffect', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)

plot(rowMeans(r2.trt.combat), rowMeans(r2.batch.combat), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), main = 'ComBat', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)

plot(rowMeans(r2.trt.plsdab), rowMeans(r2.batch.plsdab), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), main = 'PLSDA-batch', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)

plot(rowMeans(r2.trt.splsdab), rowMeans(r2.batch.splsdab), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), main = 'sPLSDA-batch', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)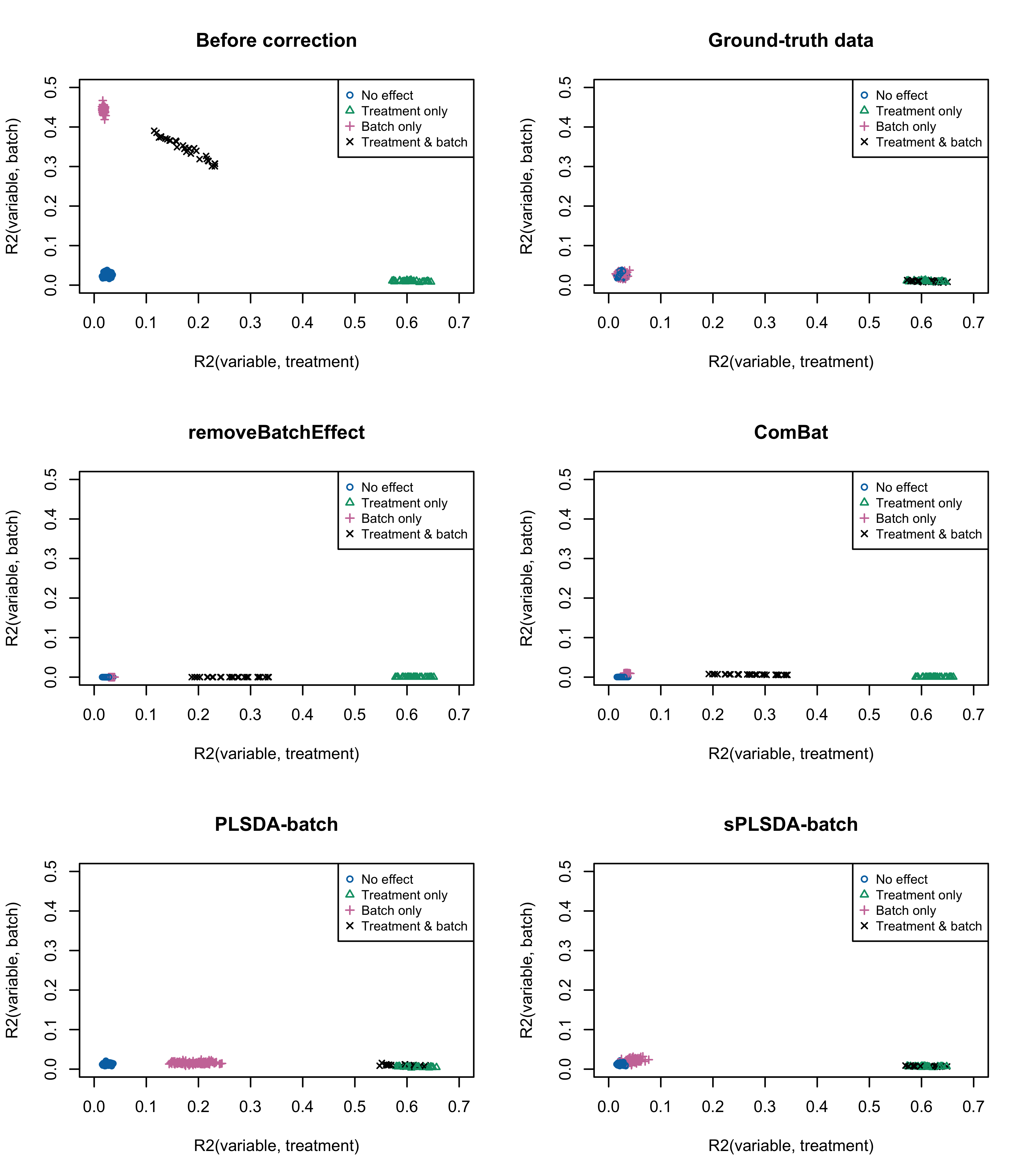
Figure 2: Simulation studies (Gaussian distribution): R2 values for each microbial variable before and after batch effect correction for the balanced batch × treatment design.

Figure 3.2: Figure 2: Simulation studies (Gaussian distribution): R2 values for each microbial variable before and after batch effect correction for the balanced batch × treatment design. 

par(mfrow = c(1,1))

We also estimated the proportion of variance explained by treatment and batch effects for each variable respectively using the \(R^2\) value. The variables assigned with both treatment and batch effects in the corrected data from removeBatchEffect and ComBat presented less proportion of treatment associated variance than in the ground truth data. This result agrees with the pRDA evaluation that these two methods do not preserve enough treatment variation. After PLSDA-batch correction, variables simulated with only batch effects displayed some amount of treatment variation, but only in the case where the batch effect variability among samples was high. sPLSDA-batch outperformed all methods, with results similar to the ground-truth data.

# precision & recall & F1 (ANOVA & sPLSDA)
## mean
acc_mean <- rbind(colMeans(precision_limma), colMeans(recall_limma), 
                  colMeans(F1_limma), colMeans(precision_splsda))
rownames(acc_mean) <- c('Precision', 'Recall', 'F1', 'Multivariate selection')
colnames(acc_mean) <- c('Before correction', 'Ground-truth data', 
                        'removeBatchEffect', 'ComBat', 
                        'PLSDA-batch', 'sPLSDA-batch')
acc_mean <- format(acc_mean, digits = 2)
knitr::kable(acc_mean, caption = 'Table 3: Simulation studies (Gaussian distribution): summary of accuracy measures before and after batch correction for the balanced batch × treatment design (mean).')
Table 3.1: Table 3: Simulation studies (Gaussian distribution): summary of accuracy measures before and after batch correction for the balanced batch × treatment design (mean).
Before correction Ground-truth data removeBatchEffect ComBat PLSDA-batch sPLSDA-batch
Precision 0.98 0.95 0.94 0.93 0.56 0.86
Recall 0.74 1.00 0.87 0.88 1.00 1.00
F1 0.84 0.98 0.89 0.89 0.68 0.92
Multivariate selection 0.89 1.00 0.92 0.92 0.92 1.00

When considering the measures of accuracy with univariate one-way ANOVA, we observed that the corrected data from PLSDA-batch and sPLSDA-batch led to higher recall and lower precision than the data from removeBatchEffect and ComBat. However, the precision of sPLSDA-batch was competitive to removeBatchEffect and ComBat. Moreover, sPLSDA-batch achieved higher F1 scores and multivariate selection scores than removeBatchEffect and ComBat.

## sd
acc_sd <- rbind(apply(precision_limma, 2, sd), apply(recall_limma, 2, sd), 
                apply(F1_limma, 2, sd), apply(precision_splsda, 2, sd))
rownames(acc_sd) <- c('Precision', 'Recall', 'F1', 'Multivariate selection')
colnames(acc_sd) <- c('Before correction', 'Ground-truth data', 
                      'removeBatchEffect', 'ComBat', 
                      'PLSDA-batch', 'sPLSDA-batch')
acc_sd <- format(acc_sd, digits = 1)
knitr::kable(acc_sd, caption = 'Table 4: Simulation studies (Gaussian distribution): summary of accuracy measures before and after batch correction for the balanced batch × treatment design (standard deviation).')
Table 3.2: Table 4: Simulation studies (Gaussian distribution): summary of accuracy measures before and after batch correction for the balanced batch × treatment design (standard deviation).
Before correction Ground-truth data removeBatchEffect ComBat PLSDA-batch sPLSDA-batch
Precision 0.021 0.031 0.151 0.160 0.252 0.110
Recall 0.095 0.000 0.098 0.098 0.021 0.000
F1 0.065 0.016 0.118 0.124 0.200 0.068
Multivariate selection 0.061 0.000 0.068 0.069 0.123 0.005

The standard deviations of the multivariate selection scores were all smaller than the univariate selection scores for the different corrected data, indicating a better stability of the variables selected by multivariate sPLSDA compared to the one-way ANOVA univariate selection.

3.2.3 Unbalanced batch \(\times\) treatment design

The unbalanced design had 4 and 16 samples from batch1 and batch2 respectively in trt1, 16 and 4 samples from batch1 and batch2 in trt2 (see the table below).

Table 5: Unbalanced batch \(\times\) treatment design in the simulation study

Trt1 Trt2
Batch1 4 16
Batch2 16 4 
nitr <- 50
p_total <- 300
p_trt_relevant <- 60
p_bat_relevant <- 150

# global variance (RDA)
gvar.before <- gvar.clean <- gvar.rbe <- gvar.combat <- 
  gvar.wplsdab <- gvar.swplsdab <- gvar.plsdab <- 
  gvar.splsdab <- data.frame(treatment = NA, batch = NA,  
                             intersection = NA, 
                             residual = NA)

# individual variance (R2)
r2.trt.before <- r2.trt.clean <- r2.trt.rbe  <- r2.trt.combat <- 
  r2.trt.wplsdab <- r2.trt.swplsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                         ncol = nitr))
r2.batch.before <- r2.batch.clean <- r2.batch.rbe  <- r2.batch.combat <- 
  r2.batch.wplsdab <- r2.batch.swplsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                             ncol = nitr))

# precision & recall & F1 (ANOVA)
precision_limma <- recall_limma <- F1_limma <- 
  data.frame(before = NA, clean = NA, rbe = NA, combat = NA, 
             wplsda_batch = NA, swplsda_batch = NA)

# precision & recall & F1 (sPLSDA)
precision_splsda <- recall_splsda <- F1_splsda <- 
  data.frame(before = NA, clean = NA, rbe = NA, combat = NA, 
             wplsda_batch = NA, swplsda_batch = NA)

for(i in seq_len(nitr)){
  ### initial setup ###
  simulation <- simData_Gaussian(mean.batch = 7, sd.batch = 8, 
                                 mean.trt = 3, sd.trt = 2, 
                                 N = 40, p_total = 300, 
                                 p_trt_relevant = 60, 
                                 p_bat_relevant = 150, 
                                 percentage_overlap_samples = 0.2,
                                 percentage_overlap_variables = 0.5, seeds = i)
  
  X <- simulation$data
  trt <- simulation$Y.trt
  batch <- simulation$Y.bat
  true.trt <- simulation$true.trt
  true.batch <- simulation$true.batch
  
  Batch_Trt.factors <- data.frame(Batch = batch, Treatment = trt)
  
  ### Before correction ###
  # global variance (RDA)
  rda.before = varpart(scale(X), ~ Treatment, ~ Batch, data = Batch_Trt.factors)
  gvar.before[i, ] <- rda.before$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.before <- c()
  indiv.batch.before <- c()
  for(c in seq_len(ncol(X))){
    fit.res1 <- lm(scale(X)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.before <- c(indiv.trt.before, fit.summary1$r.squared)
    indiv.batch.before <- c(indiv.batch.before, fit.summary2$r.squared)
  }
  r2.trt.before[ ,i] <-  indiv.trt.before
  r2.batch.before[ ,i] <-  indiv.batch.before
  
  # precision & recall & F1 (ANOVA)
  fit.before <- lmFit(t(scale(X)), design = model.matrix( ~ 0 + as.factor(trt)))
  fit.before <- contrasts.fit(fit.before, contrasts = c(1,-1))
  fit.result.before <- topTable(eBayes(fit.before), number = p_total)
  otu.sig.before <- 
    rownames(fit.result.before)[fit.result.before$adj.P.Val <= 0.05]
  
  precision_limma.before <- length(intersect(true.trt, otu.sig.before))/
    length(otu.sig.before)
  recall_limma.before <- length(intersect(true.trt, otu.sig.before))/
    length(true.trt)
  F1_limma.before <- (2*precision_limma.before*recall_limma.before)/
    (precision_limma.before + recall_limma.before)
  
  ## replace NA value with 0
  if(precision_limma.before == 'NaN'){
    precision_limma.before = 0
  }
  if(F1_limma.before == 'NaN'){
    F1_limma.before = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.before_splsda <- splsda(X = X, Y = trt, 
                              ncomp = 1, keepX = length(true.trt))
  otu.dcn.before <- which(fit.before_splsda$loadings$X[,1] != 0)
  
  precision_splsda.before <- length(intersect(true.trt, otu.dcn.before))/
    length(otu.dcn.before)
  recall_splsda.before <- length(intersect(true.trt, otu.dcn.before))/
    length(true.trt)
  F1_splsda.before <- (2*precision_splsda.before*recall_splsda.before)/
    (precision_splsda.before + recall_splsda.before)
  
  ## replace NA value with 0
  if(F1_splsda.before == 'NaN'){
    F1_splsda.before = 0
  }
  
  ##############################################################################
  ### Ground-truth data ###
  X.clean <- simulation$cleanData
  # global variance (RDA)
  rda.clean = varpart(scale(X.clean), ~ Treatment, ~ Batch, 
                      data = Batch_Trt.factors)
  gvar.clean[i, ] <- rda.clean$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.clean <- c()
  indiv.batch.clean <- c()
  for(c in seq_len(ncol(X.clean))){
    fit.res1 <- lm(scale(X.clean)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.clean)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.clean <- c(indiv.trt.clean, fit.summary1$r.squared)
    indiv.batch.clean <- c(indiv.batch.clean, fit.summary2$r.squared)
  }
  r2.trt.clean[ ,i] <-  indiv.trt.clean
  r2.batch.clean[ ,i] <-  indiv.batch.clean
  
  # precision & recall & F1 (ANOVA)
  fit.clean <- lmFit(t(scale(X.clean)), 
                     design = model.matrix( ~ 0 + as.factor(trt)))
  fit.clean <- contrasts.fit(fit.clean, contrasts = c(1,-1))
  fit.result.clean <- topTable(eBayes(fit.clean), number = p_total)
  otu.sig.clean <- 
    rownames(fit.result.clean)[fit.result.clean$adj.P.Val <= 0.05]
  
  precision_limma.clean <- length(intersect(true.trt, otu.sig.clean))/
    length(otu.sig.clean)
  recall_limma.clean <- length(intersect(true.trt, otu.sig.clean))/
    length(true.trt)
  F1_limma.clean <- (2*precision_limma.clean*recall_limma.clean)/
    (precision_limma.clean + recall_limma.clean)
  
  ## replace NA value with 0
  if(precision_limma.clean == 'NaN'){
    precision_limma.clean = 0
  }
  if(F1_limma.clean == 'NaN'){
    F1_limma.clean = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.clean_splsda <- splsda(X = X.clean, Y = trt, ncomp = 1, 
                             keepX = length(true.trt))
  otu.dcn.clean <- which(fit.clean_splsda$loadings$X[ ,1] != 0)
  
  precision_splsda.clean <- length(intersect(true.trt, otu.dcn.clean))/
    length(otu.dcn.clean)
  recall_splsda.clean <- length(intersect(true.trt, otu.dcn.clean))/
    length(true.trt)
  F1_splsda.clean <- (2*precision_splsda.clean*recall_splsda.clean)/
    (precision_splsda.clean + recall_splsda.clean)
  
  ## replace NA value with 0
  if(F1_splsda.clean == 'NaN'){
    F1_splsda.clean = 0
  }
  
  ##############################################################################
  ### removeBatchEffect corrected data ###
  X.rbe <-t(removeBatchEffect(t(X), batch = batch, 
                              design = model.matrix( ~ 0 + as.factor(trt))))
  
  # global variance (RDA)
  rda.rbe = varpart(scale(X.rbe), ~ Treatment, ~ Batch, 
                    data = Batch_Trt.factors)
  gvar.rbe[i, ] <- rda.rbe$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.rbe <- c()
  indiv.batch.rbe <- c()
  for(c in seq_len(ncol(X.rbe))){
    fit.res1 <- lm(scale(X.rbe)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.rbe)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.rbe <- c(indiv.trt.rbe, fit.summary1$r.squared)
    indiv.batch.rbe <- c(indiv.batch.rbe, fit.summary2$r.squared)
  }
  r2.trt.rbe[ ,i] <-  indiv.trt.rbe
  r2.batch.rbe[ ,i] <-  indiv.batch.rbe
  
  # precision & recall & F1 (ANOVA)
  fit.rbe <- lmFit(t(scale(X.rbe)), 
                   design = model.matrix( ~ 0 + as.factor(trt)))
  fit.rbe <- contrasts.fit(fit.rbe, contrasts = c(1,-1))
  fit.result.rbe <- topTable(eBayes(fit.rbe), number = p_total)
  otu.sig.rbe <- rownames(fit.result.rbe)[fit.result.rbe$adj.P.Val <= 0.05]
  
  precision_limma.rbe <- length(intersect(true.trt, otu.sig.rbe))/
    length(otu.sig.rbe)
  recall_limma.rbe <- length(intersect(true.trt, otu.sig.rbe))/
    length(true.trt)
  F1_limma.rbe <- (2*precision_limma.rbe*recall_limma.rbe)/
    (precision_limma.rbe + recall_limma.rbe)
  
  ## replace NA value with 0
  if(precision_limma.rbe == 'NaN'){
    precision_limma.rbe = 0
  }
  if(F1_limma.rbe == 'NaN'){
    F1_limma.rbe = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.rbe_splsda <- splsda(X = X.rbe, Y = trt, 
                           ncomp = 1, keepX = length(true.trt))
  otu.dcn.rbe <- which(fit.rbe_splsda$loadings$X[ ,1] != 0)
  
  precision_splsda.rbe <- length(intersect(true.trt, otu.dcn.rbe))/
    length(otu.dcn.rbe)
  recall_splsda.rbe <- length(intersect(true.trt, otu.dcn.rbe))/
    length(true.trt)
  F1_splsda.rbe <- (2*precision_splsda.rbe*recall_splsda.rbe)/
    (precision_splsda.rbe + recall_splsda.rbe)
  
  ## replace NA value with 0
  if(F1_splsda.rbe == 'NaN'){
    F1_splsda.rbe = 0
  }
  
  ##############################################################################
  ### ComBat corrected data ###
  X.combat <- t(ComBat(dat = t(X), batch = batch, 
                       mod = model.matrix( ~ as.factor(trt))))
  
  # global variance (RDA)
  rda.combat = varpart(scale(X.combat), ~ Treatment, ~ Batch, 
                       data = Batch_Trt.factors)
  gvar.combat[i, ] <- rda.combat$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.combat <- c()
  indiv.batch.combat <- c()
  for(c in seq_len(ncol(X.combat))){
    fit.res1 <- lm(scale(X.combat)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.combat)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.combat <- c(indiv.trt.combat, fit.summary1$r.squared)
    indiv.batch.combat <- c(indiv.batch.combat, fit.summary2$r.squared)
  }
  r2.trt.combat[ ,i] <-  indiv.trt.combat
  r2.batch.combat[ ,i] <-  indiv.batch.combat
  
  # precision & recall & F1 (ANOVA)
  fit.combat <- lmFit(t(scale(X.combat)), 
                      design = model.matrix( ~ 0 + as.factor(trt)))
  fit.combat <- contrasts.fit(fit.combat, contrasts = c(1,-1))
  fit.result.combat <- topTable(eBayes(fit.combat), number = p_total)
  otu.sig.combat <- 
    rownames(fit.result.combat)[fit.result.combat$adj.P.Val <= 0.05]
  
  precision_limma.combat <- length(intersect(true.trt, otu.sig.combat))/
    length(otu.sig.combat)
  recall_limma.combat <- length(intersect(true.trt, otu.sig.combat))/
    length(true.trt)
  F1_limma.combat <- (2*precision_limma.combat*recall_limma.combat)/
    (precision_limma.combat + recall_limma.combat)
  
  ## replace NA value with 0
  if(precision_limma.combat == 'NaN'){
    precision_limma.combat = 0
  }
  if(F1_limma.combat == 'NaN'){
    F1_limma.combat = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.combat_splsda <- splsda(X = X.combat, Y = trt, ncomp = 1, 
                              keepX = length(true.trt))
  otu.dcn.combat <- which(fit.combat_splsda$loadings$X[ ,1] != 0)
  
  precision_splsda.combat <- length(intersect(true.trt, otu.dcn.combat))/
    length(otu.dcn.combat)
  recall_splsda.combat <- length(intersect(true.trt, otu.dcn.combat))/
    length(true.trt)
  F1_splsda.combat <- (2*precision_splsda.combat*recall_splsda.combat)/
    (precision_splsda.combat + recall_splsda.combat)
  
  ## replace NA value with 0
  if(F1_splsda.combat == 'NaN'){
    F1_splsda.combat = 0
  }
  
  ##############################################################################
  ### wPLSDA-batch corrected data ###
  X.wplsda_batch.correct <- PLSDA_batch(X = X, 
                                        Y.trt = trt, Y.bat = batch, 
                                        ncomp.trt = 1, ncomp.bat = 1,
                                        balance = FALSE)
  X.wplsda_batch <- X.wplsda_batch.correct$X.nobatch
  colnames(X.wplsda_batch) <- seq_len(p_total)
  
  # global variance (RDA)
  rda.wplsda_batch = varpart(scale(X.wplsda_batch), ~ Treatment, ~ Batch, 
                             data = Batch_Trt.factors)
  gvar.wplsdab[i, ] <- rda.wplsda_batch$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.wplsda_batch <- c()
  indiv.batch.wplsda_batch <- c()
  for(c in seq_len(ncol(X.wplsda_batch))){
    fit.res1 <- lm(scale(X.wplsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.wplsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.wplsda_batch <- c(indiv.trt.wplsda_batch, fit.summary1$r.squared)
    indiv.batch.wplsda_batch <- c(indiv.batch.wplsda_batch, 
                                  fit.summary2$r.squared)
  }
  r2.trt.wplsdab[ ,i] <-  indiv.trt.wplsda_batch
  r2.batch.wplsdab[ ,i] <-  indiv.batch.wplsda_batch
  
  # precision & recall & F1 (ANOVA)
  fit.wplsda_batch <- lmFit(t(scale(X.wplsda_batch)), 
                            design = model.matrix( ~ 0 + as.factor(trt)))
  fit.wplsda_batch <- contrasts.fit(fit.wplsda_batch, contrasts = c(1,-1))
  fit.result.wplsda_batch <- topTable(eBayes(fit.wplsda_batch), 
                                      number = p_total)
  otu.sig.wplsda_batch <- rownames(fit.result.wplsda_batch)[
    fit.result.wplsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.wplsda_batch <- 
    length(intersect(true.trt, otu.sig.wplsda_batch))/
    length(otu.sig.wplsda_batch)
  recall_limma.wplsda_batch <- 
    length(intersect(true.trt, otu.sig.wplsda_batch))/
    length(true.trt)
  F1_limma.wplsda_batch <- 
    (2*precision_limma.wplsda_batch*recall_limma.wplsda_batch)/
    (precision_limma.wplsda_batch + recall_limma.wplsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.wplsda_batch == 'NaN'){
    precision_limma.wplsda_batch = 0
  }
  if(F1_limma.wplsda_batch == 'NaN'){
    F1_limma.wplsda_batch = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.wplsda_batch_splsda <- splsda(X = X.wplsda_batch, Y = trt, ncomp = 1, 
                                    keepX = length(true.trt))
  otu.dcn.wplsda_batch <- which(fit.wplsda_batch_splsda$loadings$X[ ,1] != 0)
  
  precision_splsda.wplsda_batch <- 
    length(intersect(true.trt, otu.dcn.wplsda_batch))/
    length(otu.dcn.wplsda_batch)
  recall_splsda.wplsda_batch <- 
    length(intersect(true.trt, otu.dcn.wplsda_batch))/
    length(true.trt)
  F1_splsda.wplsda_batch <- 
    (2*precision_splsda.wplsda_batch*recall_splsda.wplsda_batch)/
    (precision_splsda.wplsda_batch + recall_splsda.wplsda_batch)
  
  ## replace NA value with 0
  if(F1_splsda.wplsda_batch == 'NaN'){
    F1_splsda.wplsda_batch = 0
  }
  
  ##############################################################################
  ### swPLSDA-batch corrected data ###
  X.swplsda_batch.correct <- PLSDA_batch(X = X, 
                                         Y.trt = trt, Y.bat = batch, 
                                         ncomp.trt = 1, 
                                         keepX.trt = length(true.trt), 
                                         ncomp.bat = 1, balance = FALSE)
  X.swplsda_batch <- X.swplsda_batch.correct$X.nobatch
  colnames(X.swplsda_batch) <- seq_len(p_total)
  
  # global variance (RDA)
  rda.swplsda_batch = varpart(scale(X.swplsda_batch), ~ Treatment, ~ Batch, 
                              data = Batch_Trt.factors)
  gvar.swplsdab[i, ] <- rda.swplsda_batch$part$indfract$Adj.R.squared
  
  # individual variance (R2)
  indiv.trt.swplsda_batch <- c()
  indiv.batch.swplsda_batch <- c()
  for(c in seq_len(ncol(X.swplsda_batch))){
    fit.res1 <- lm(scale(X.swplsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.swplsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.swplsda_batch <- c(indiv.trt.swplsda_batch, 
                                 fit.summary1$r.squared)
    indiv.batch.swplsda_batch <- c(indiv.batch.swplsda_batch, 
                                   fit.summary2$r.squared)
  }
  r2.trt.swplsdab[ ,i] <-  indiv.trt.swplsda_batch
  r2.batch.swplsdab[ ,i] <-  indiv.batch.swplsda_batch
  
  # precision & recall & F1 (ANOVA)
  fit.swplsda_batch <- lmFit(t(scale(X.swplsda_batch)), 
                             design = model.matrix( ~ 0 + as.factor(trt)))
  fit.swplsda_batch <- contrasts.fit(fit.swplsda_batch, contrasts = c(1,-1))
  fit.result.swplsda_batch <- topTable(eBayes(fit.swplsda_batch), 
                                       number = p_total)
  otu.sig.swplsda_batch <- rownames(fit.result.swplsda_batch)[
    fit.result.swplsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.swplsda_batch <- 
    length(intersect(true.trt, otu.sig.swplsda_batch))/
    length(otu.sig.swplsda_batch)
  recall_limma.swplsda_batch <- 
    length(intersect(true.trt, otu.sig.swplsda_batch))/
    length(true.trt)
  F1_limma.swplsda_batch <- 
    (2*precision_limma.swplsda_batch*recall_limma.swplsda_batch)/
    (precision_limma.swplsda_batch + recall_limma.swplsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.swplsda_batch == 'NaN'){
    precision_limma.swplsda_batch = 0
  }
  if(F1_limma.swplsda_batch == 'NaN'){
    F1_limma.swplsda_batch = 0
  }
  
  # precision & recall & F1 (sPLSDA)
  fit.swplsda_batch_splsda <- splsda(X = X.swplsda_batch, Y = trt, ncomp = 1, 
                                     keepX = length(true.trt))
  otu.dcn.swplsda_batch <- which(fit.swplsda_batch_splsda$loadings$X[ ,1] != 0)
  
  precision_splsda.swplsda_batch <- 
    length(intersect(true.trt, otu.dcn.swplsda_batch))/
    length(otu.dcn.swplsda_batch)
  recall_splsda.swplsda_batch <- 
    length(intersect(true.trt, otu.dcn.swplsda_batch))/
    length(true.trt)
  F1_splsda.swplsda_batch <- 
    (2*precision_splsda.swplsda_batch*recall_splsda.swplsda_batch)/
    (precision_splsda.swplsda_batch + recall_splsda.swplsda_batch)
  
  ## replace NA value with 0
  if(F1_splsda.swplsda_batch == 'NaN'){
    F1_splsda.swplsda_batch = 0
  }
  
  ##############################################################################
  ### PLSDA-batch corrected data ###
  X.plsda_batch.correct <- PLSDA_batch(X = X, 
                                       Y.trt = trt, Y.bat = batch, 
                                       ncomp.trt = 1, ncomp.bat = 1)
  X.plsda_batch <- X.plsda_batch.correct$X.nobatch
  colnames(X.plsda_batch) <- seq_len(p_total)
  
  # global variance (RDA)
  rda.plsda_batch = varpart(scale(X.plsda_batch), ~ Treatment, ~ Batch, 
                            data = Batch_Trt.factors)
  gvar.plsdab[i, ] <- rda.plsda_batch$part$indfract$Adj.R.squared
  
  ##############################################################################
  ### sPLSDA-batch corrected data ###
  X.splsda_batch.correct <- PLSDA_batch(X = X, 
                                        Y.trt = trt, Y.bat = batch, 
                                        ncomp.trt = 1, 
                                        keepX.trt = length(true.trt), 
                                        ncomp.bat = 1)
  X.splsda_batch <- X.splsda_batch.correct$X.nobatch
  colnames(X.splsda_batch) <- seq_len(p_total)
  
  # global variance (RDA)
  rda.splsda_batch = varpart(scale(X.splsda_batch), ~ Treatment, ~ Batch,
                             data = Batch_Trt.factors)
  gvar.splsdab[i, ] <- rda.splsda_batch$part$indfract$Adj.R.squared
  
  
  # summary
  # precision & recall & F1 (ANOVA)
  precision_limma[i, ] <- c(`Before correction` = precision_limma.before, 
                            `Ground-truth data` = precision_limma.clean,
                            `removeBatchEffect` = precision_limma.rbe,
                            ComBat = precision_limma.combat,
                            `wPLSDA-batch` = precision_limma.wplsda_batch,
                            `swPLSDA-batch` = precision_limma.swplsda_batch)
  
  recall_limma[i, ] <- c(`Before correction` = recall_limma.before, 
                         `Ground-truth data` = recall_limma.clean,
                         `removeBatchEffect` = recall_limma.rbe,
                         ComBat = recall_limma.combat,
                         `wPLSDA-batch` = recall_limma.wplsda_batch,
                         `swPLSDA-batch` = recall_limma.swplsda_batch)
  
  F1_limma[i, ] <- c(`Before correction` = F1_limma.before, 
                     `Ground-truth data` = F1_limma.clean,
                     `removeBatchEffect` = F1_limma.rbe,
                     ComBat = F1_limma.combat,
                     `wPLSDA-batch` = F1_limma.wplsda_batch,
                     `swPLSDA-batch` = F1_limma.swplsda_batch)
  
  
  # precision & recall & F1 (sPLSDA)
  precision_splsda[i, ] <- c(`Before correction` = precision_splsda.before, 
                             `Ground-truth data` = precision_splsda.clean,
                             `removeBatchEffect` = precision_splsda.rbe,
                             ComBat = precision_splsda.combat,
                             `wPLSDA-batch` = precision_splsda.wplsda_batch,
                             `swPLSDA-batch` = precision_splsda.swplsda_batch)
  
  recall_splsda[i, ] <- c(`Before correction` = recall_splsda.before, 
                          `Ground-truth data` = recall_splsda.clean,
                          `removeBatchEffect` = recall_splsda.rbe,
                          ComBat = recall_splsda.combat,
                          `wPLSDA-batch` = recall_splsda.wplsda_batch,
                          `swPLSDA-batch` = recall_splsda.swplsda_batch)
  
  F1_splsda[i, ] <- c(`Before correction` = F1_splsda.before, 
                      `Ground-truth data` = F1_splsda.clean,
                      `removeBatchEffect` = F1_splsda.rbe,
                      ComBat = F1_splsda.combat,
                      `wPLSDA-batch` = F1_splsda.wplsda_batch,
                      `swPLSDA-batch` = F1_splsda.swplsda_batch)
  
}

3.2.4 Figures

# global variance (RDA)
prop.gvar.all <- rbind(`Before correction` = colMeans(gvar.before),
                       `Ground-truth data` = colMeans(gvar.clean),
                       removeBatchEffect = colMeans(gvar.rbe),
                       ComBat = colMeans(gvar.combat),
                       `wPLSDA-batch` = colMeans(gvar.wplsdab),
                       `swPLSDA-batch` = colMeans(gvar.swplsdab),
                       `PLSDA-batch` = colMeans(gvar.plsdab),
                       `sPLSDA-batch` = colMeans(gvar.splsdab))

prop.gvar.all[prop.gvar.all < 0] = 0
prop.gvar.all <- t(apply(prop.gvar.all, 1, function(x){x/sum(x)}))
colnames(prop.gvar.all) <- c('Treatment', 'Intersection', 'Batch', 'Residuals')

partVar_plot(prop.df = prop.gvar.all)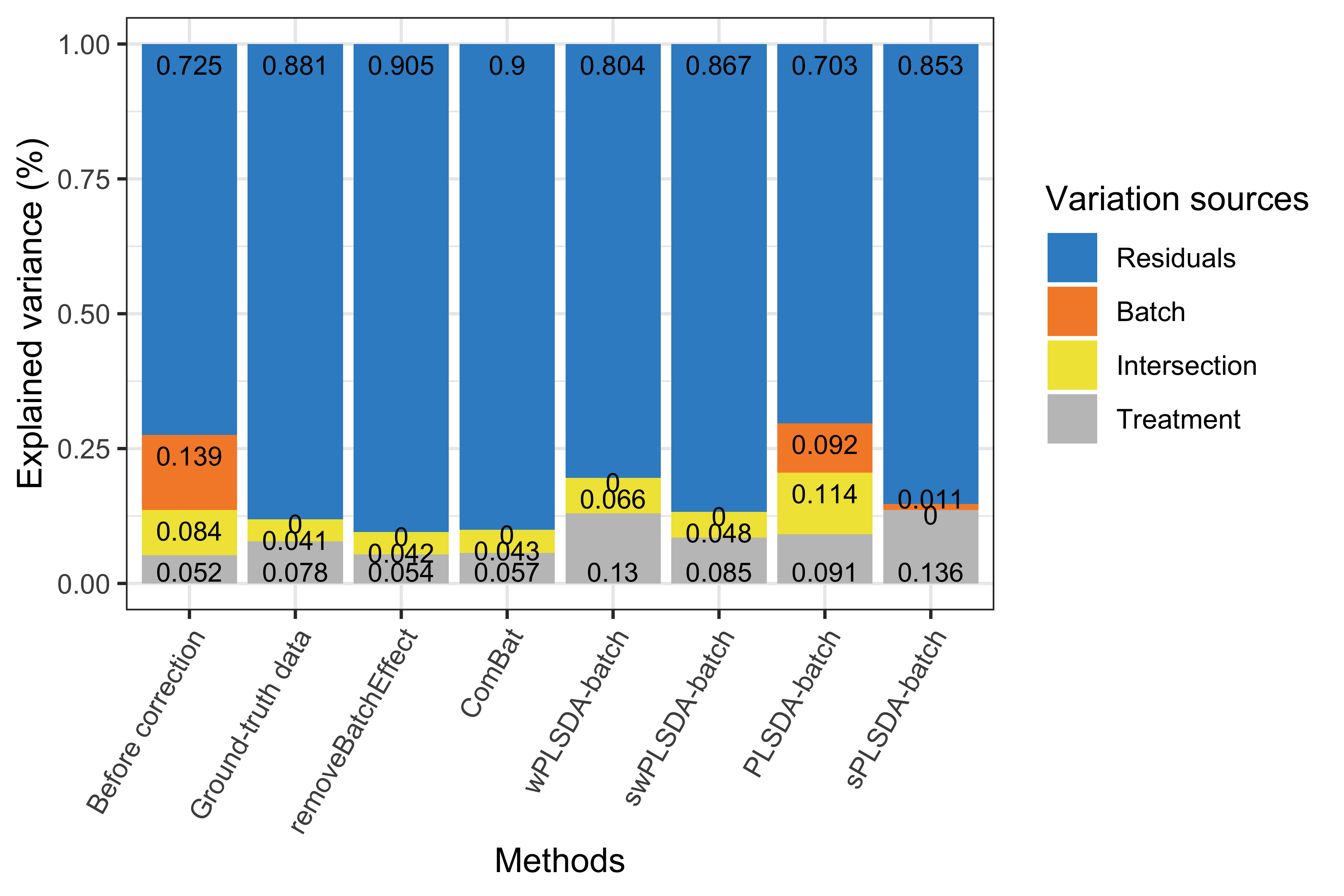
Figure 3: Simulation studies (Gaussian distribution): comparison of explained variance before and after batch effect correction for the unbalanced batch × treatment design.

Figure 3.3: Figure 3: Simulation studies (Gaussian distribution): comparison of explained variance before and after batch effect correction for the unbalanced batch × treatment design.

With an unbalanced batch \(\times\) treatment design, we observed that certain amount of variance was shared (intersection) and explained by both batch and treatment effects. Such intersectional variance should exist even in the ground-truth data with no batch effect, as it originates from treatment variation because of the unbalanced design. Unweighted PLSDA-batch and sPLSDA-batch failed in such design, as their corrected data still included a large amount of batch variation (PLSDA-batch) or not included intersectional variance (sPLSDA-batch), while the other methods removed batch variation successfully. The corrected data from removeBatchEffect and ComBat included less proportion of variance explained by treatment but more intersectional variance compared to the ground-truth data. Although wPLSDA-batch corrected data included the largest treatment variance, swPLSDA-batch outperformed all methods with results similar to the ground-truth data.

################################################################################
# individual variance (R2)
# color
gcolor <- c(rep(pb_color(16), p_trt_relevant), 
            rep(pb_color(17), (p_total - p_trt_relevant)))
gcolor[intersect(true.trt, true.batch)] = pb_color(18)
gcolor[setdiff(seq_len(p_total), union(true.trt, true.batch))] = pb_color(15)

xlabs = 'R2(variable, treatment)'
ylabs = 'R2(variable, batch)'
edgex = 0.7
edgey = 0.6

# scatterplot
par(mfrow = c(3,2))
plot(rowMeans(r2.trt.before), rowMeans(r2.batch.before), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), 
     main = 'Before correction', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)

plot(rowMeans(r2.trt.clean), rowMeans(r2.batch.clean), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), 
     main = 'Ground-truth data', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)

plot(rowMeans(r2.trt.rbe), rowMeans(r2.batch.rbe), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), 
     main = 'removeBatchEffect', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)

plot(rowMeans(r2.trt.combat), rowMeans(r2.batch.combat), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), main = 'ComBat', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)

plot(rowMeans(r2.trt.wplsdab), rowMeans(r2.batch.wplsdab), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), main = 'wPLSDA-batch', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)

plot(rowMeans(r2.trt.swplsdab), rowMeans(r2.batch.swplsdab), col = gcolor, 
     xlab = xlabs, ylab = ylabs, pch = as.numeric(as.factor(gcolor)),
     xlim = c(0, edgex), ylim = c(0, edgey), main = 'swPLSDA-batch', cex = 0.7)
legend('topright', legend = c('No effect', 'Treatment only', 
                              'Batch only', 'Treatment & batch'), 
       col = pb_color(15:18), pch = seq_len(4), cex = 0.8)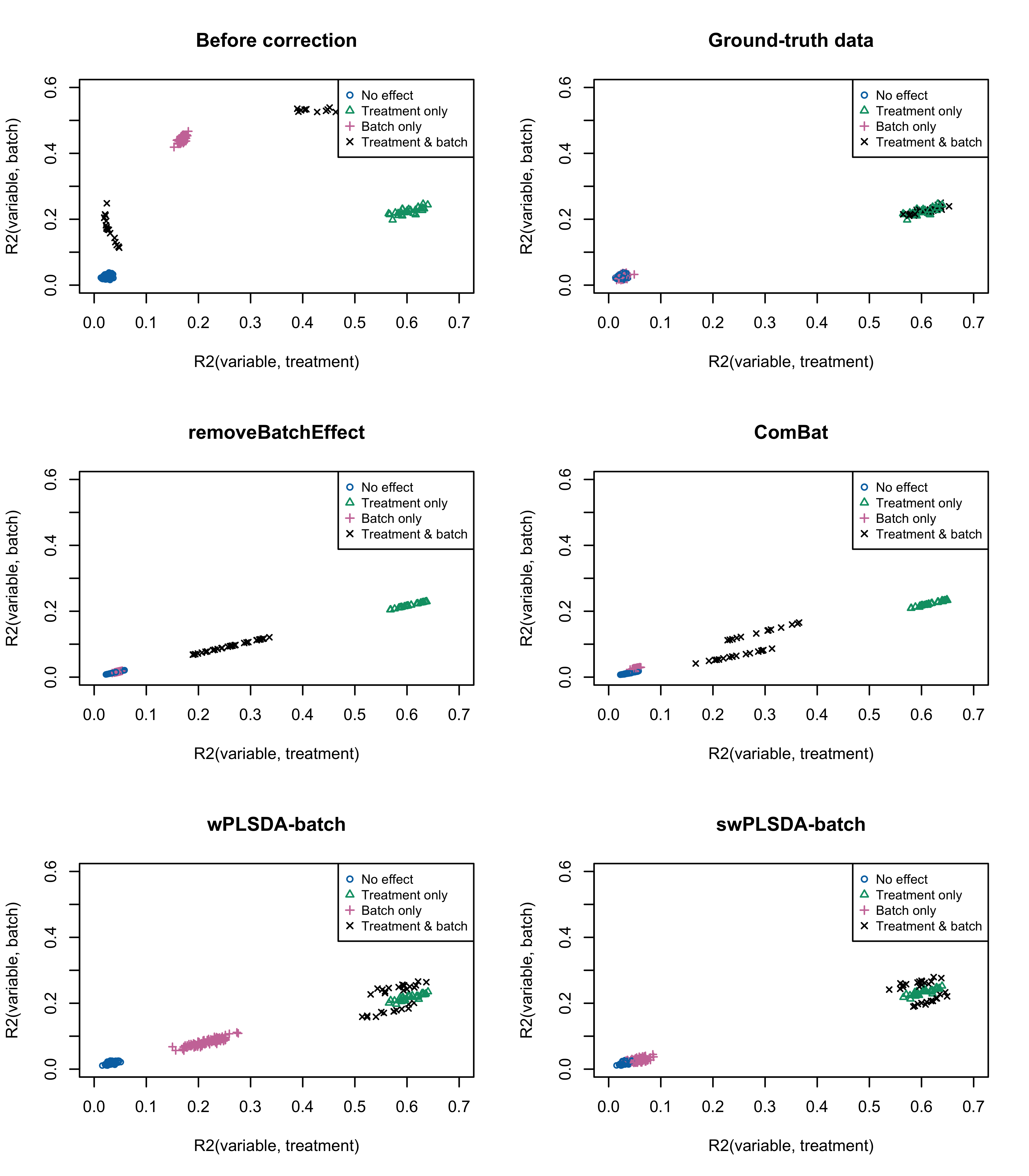
Figure 4: Simulation studies (Gaussian distribution): R2 values for each microbial variable before and after batch effect correction for the unbalanced batch × treatment design.

Figure 3.4: Figure 4: Simulation studies (Gaussian distribution): R2 values for each microbial variable before and after batch effect correction for the unbalanced batch × treatment design. 

par(mfrow = c(1,1))

Based on the \(R^2\) values, variables assigned with both treatment and batch effects were segregated into two groups depending on whether their abundance increased or decreased consistently or not according to the two effects. We observed similar results to those obtained from the balanced design.

# precision & recall & F1 (ANOVA & sPLSDA)
## mean
acc_mean <- rbind(colMeans(precision_limma), colMeans(recall_limma), 
                  colMeans(F1_limma), colMeans(precision_splsda))
rownames(acc_mean) <- c('Precision', 'Recall', 'F1', 'Multivariate selection')
colnames(acc_mean) <- c('Before correction', 'Ground-truth data', 
                        'removeBatchEffect', 'ComBat', 
                        'wPLSDA-batch', 'swPLSDA-batch')
acc_mean <- format(acc_mean, digits = 2)
knitr::kable(acc_mean, caption = 'Table 6: Simulation studies (Gaussian distribution): summary of accuracy measures before and after batch correction for the unbalanced batch × treatment design (mean).')
Table 3.3: Table 6: Simulation studies (Gaussian distribution): summary of accuracy measures before and after batch correction for the unbalanced batch × treatment design (mean).
Before correction Ground-truth data removeBatchEffect ComBat wPLSDA-batch swPLSDA-batch
Precision 0.52 0.96 0.85 0.80 0.52 0.80
Recall 0.72 1.00 0.86 0.86 0.99 1.00
F1 0.55 0.98 0.84 0.81 0.65 0.88
Multivariate selection 0.73 1.00 0.88 0.87 0.89 0.99

When considering the measures of accuracy with univariate one-way ANOVA, we observed that the corrected data from wPLSDA-batch and swPLSDA-batch led to higher recall and lower precision than the data from removeBatchEffect and ComBat. However, the precision of swPLSDA-batch was competitive to removeBatchEffect and ComBat. Moreover, weighted sPLSDA-batch achieved higher F1 scores and multivariate selection scores than removeBatchEffect and ComBat.

## sd
acc_sd <- rbind(apply(precision_limma, 2, sd), apply(recall_limma, 2, sd), 
                apply(F1_limma, 2, sd), apply(precision_splsda, 2, sd))
rownames(acc_sd) <- c('Precision', 'Recall', 'F1', 'Multivariate selection')
colnames(acc_sd) <- c('Before correction', 'Ground-truth data', 
                      'removeBatchEffect', 'ComBat', 
                      'wPLSDA-batch', 'swPLSDA-batch')
acc_sd <- format(acc_sd, digits = 2)
knitr::kable(acc_sd, caption = 'Table 7: Simulation studies (Gaussian distribution): summary of accuracy measures before and after batch correction for the unbalanced batch × treatment design (standard deviation).')
Table 3.4: Table 7: Simulation studies (Gaussian distribution): summary of accuracy measures before and after batch correction for the unbalanced batch × treatment design (standard deviation).
Before correction Ground-truth data removeBatchEffect ComBat wPLSDA-batch swPLSDA-batch
Precision 0.325 0.031 0.176 0.231 0.232 0.137
Recall 0.042 0.000 0.104 0.100 0.029 0.000
F1 0.212 0.017 0.137 0.177 0.189 0.092
Multivariate selection 0.051 0.000 0.069 0.083 0.148 0.016

The standard deviations of the multivariate selection scores were all smaller than the univariate selection scores for the different corrected data, indicating a better stability of the variables selected by multivariate sPLSDA compared to the one-way ANOVA univariate selection.

3.3 References

References

Singh, Amrit, Casey P Shannon, Benoı̂t Gautier, Florian Rohart, Michaël Vacher, Scott J Tebbutt, and Kim-Anh Lê Cao. 2019. “DIABLO: An Integrative Approach for Identifying Key Molecular Drivers from Multi-Omics Assays.” Bioinformatics 35 (17): 3055–62.
Weiss, Sophie, Zhenjiang Zech Xu, Shyamal Peddada, Amnon Amir, Kyle Bittinger, Antonio Gonzalez, Catherine Lozupone, et al. 2017. “Normalization and Microbial Differential Abundance Strategies Depend Upon Data Characteristics.” Microbiome 5 (1): 1–18.