Chapter 4 Batch Effects Management in Simulation Studies (Negative Binomial Distribution)

4.1 Introduction

Microbiome data are multivariate with inherent correlation structure between microbial variables. The data are over-dispersed with a distribution close to a negative binomial distribution (McMurdie and Holmes 2014; Quinn et al. 2018). Inspired by (Hawinkel et al. 2019), we simulated data from multivariate negative binomial distribution achieved with quantile-quantile transformation between multivariate normal and negative binomial distributions. To add treatment and batch effects, we used matrix factorisation to simulate the mean for modelling negative binomial distribution as a matrix \[\Theta = \begin{bmatrix} \theta_{11} & ... & \theta_{1M}\\ ...& ... & ... \\ \theta_{1N} & ... & \theta_{NM} \end{bmatrix}\] for \(N\) samples and \(M\) microbial variables as follows:

\[\Theta = exp(x_{(trt)}^{\top}\beta^{(trt)} + x_{(batch)}^{\top}\beta^{(batch)} + \epsilon)\]

where \(x_{(trt)}\) and \(x_{(batch)}\) represent the design vectors of treatment and batch effects respectively for each sample. \(\beta^{(trt)}\) and \(\beta^{(batch)}\) represent the regression coefficients of treatment and batch effects for each microbial variable, and \(\beta^{(trt)}_{j} \in N(\mu_{(trt)},\sigma_{(trt)}^{2})\), \(\beta^{(batch)}_{j} \in N(\mu_{(batch)},\sigma_{(batch)}^{2})\). \(\epsilon\) contains the random noise that is independent and identically distributed (i.i.d) and \(\epsilon_{ij} \in N(0,\delta^{2})\), in which \(i = 1,2,...,N\) samples, \(j = 1,2,..,M\) variables.

The probability matrix \[P = \begin{bmatrix} p_{11} & ... & p_{1M}\\ ...& ... & ... \\ p_{1N} & ... & p_{NM} \end{bmatrix}\] for modelling negative binomial distribution is calculated as

\[p_{ij} = \frac{r}{r + \theta_{ij}}\] where \(p_{ij}\) and \(\theta_{ij}\) represent the probability of success in each trial and the mean for negative binomial distribution of sample \(i\) and microbial variable \(j\), and \(r\) is the dispersion parameter representing the number of successes.

We then simulated a data matrix based on multivariate normal distribution with mean \(0\) and correlation matrix \(\Sigma\):

\[X^{normal} = N(0, \Sigma)\]

where the correlation matrix \(\Sigma\) was simulated with the strategy adapted from (McGregor, Labbe, and Greenwood 2020) as follows: We first generated a lower-triangular matrix \(L\), in which the diagonal elements follow \(Unif(1.5, 2.5)\), and the other elements \(Unif(-1.5, 1.5)\). We randomly set the elements outside the diagonal of \(L\) to zero with probability \(0.7\). A precision matrix, which is the inverse of covariance matrix was created as \(R^{-1} = LL^{\top}\). The corresponding correlation matrix \(\Sigma\) to \(R\) was then obtained. These parameters were set according to (McGregor, Labbe, and Greenwood 2020).

Thereafter we used Cumulative Distribution Function (CDF) to achieve quantile-quantile transformation as:

\[CDF(x^{normal}_{ij}) = CDF(x^{nb}_{ij})\]

where \(CDF(x^{normal}_{ij})\) represents the cumulative probability of \(x^{normal}_{ij}\) for sample \(i\) and variable \(j\) that belongs to matrix \(X^{normal}\) from multivariate normal distribution. \(CDF(x^{nb}_{ij})\) represents the cumulative probability of each \(x^{nb}_{ij}\) in matrix \(X^{nb}\) from negative binomial distribution.

Based on the cumulative probability, we can simulate a data matrix \(X^{nb}\) with multivariate negative binomial distribution:

\[X^{nb} = NB(r, P, \Sigma)\]

where \(r\) represents the dispersion parameter, \(P\) represents the probability matrix and \(\Sigma\) the correlation matrix explaining the dependence structure between microbial variables.

We simulated datasets with different parameters including amount of batch and treatment effects (\(\mu_{(batch)}\), \(\mu_{(trt)}\)) and variability among variables (\(\sigma_{(batch)}\), \(\sigma_{(trt)}\)), number of variables with batch and/or treatment effects (\(M^{(batch)}\), \(M^{(trt)}\) and \(M^{(trt \ \& \ batch)}\)), balanced and unbalanced batch \(\times\) treatment designs, as summarised in the table below.

Table 1: Summary of simulation scenarios (Negative Binomial distribution). For a given choice of parameters reported in this table, each simulation was repeated 50 times. \(M^{(trt)}, M^{(batch)}\) and \(M^{(trt \ \& \ batch)}\) represent the number of variables with treatment, batch, or both effects respectively. Simu 6 includes parameters likely to represent real data according to our experience in analysing microbiome datasets.

\(\mu_{(trt)}\) \(\sigma_{(trt)}\) \(\mu_{(batch)}\) \(\sigma_{(batch)}\) \(M^{(trt)}\) \(M^{(batch)}\) \(M^{(trt \ \& \ batch)}\)
Simu 1 3 1 7 {1,4,8} 60 150 0
Simu 2 {3,5,7} 1 7 8 60 150 0
Simu 3 3 {1,2,4} 7 8 60 150 0
Simu 4 3 2 7 8 {30,60,100,150} 150 0
Simu 5 3 2 7 8 60 {30,60,100,150} 0
Simu 6 3 2 7 8 60 150 {0,18,30,42,60}

The microbial variables with treatment or batch effects were randomly indexed in the data with non-zero \(\beta^{(trt)}\) or \(\beta^{(batch)}\). The background noise \(\epsilon_{ij}\) was randomly sampled from \(N(0,0.2^{2})\), reflecting real microbiome datasets.

We also simulated datasets with different number of batch groups:

  1. Two batch groups: Each dataset included 300 variables and 40 samples grouped according to two treatments (trt1 and trt2) and two batches (batch1 and batch2).
  2. Three batch groups: Each dataset included 300 variables and 36 samples grouped according to two treatments (trt1 and trt2) and three batches (batch1, batch2 and batch3).

In addition, we simulated a ground-truth dataset that only included treatment effects and background noise without batch effects to evaluate batch effect correction methods.

Our simulations generate over-dispersed count data with batch and treatment effects as well as correlation structure among variables, but without any compositional structure. We therefore only applied natural log transformation to the simulated data prior to analysis.

In these simulation scenarios, for PLSDA-batch we set \(C-1\) (or \(B-1\)) components associated with treatment (or batch) effects (where \(C\) and \(B\) represent the total number of treatment and batch groups respectively) as \(C-1\) (\(B-1\)) components are likely to explain 100% variance in \(Y\). The number of variables with a true treatment effect (\(M^{(trt)}\)) is set as the optimal number to select on each treatment component in sPLSDA-batch.

4.2 Simulations (two batch groups)

4.2.1 Balanced batch \(\times\) treatment design

The balanced batch \(\times\) treatment experimental design included 10 samples from two batches respectively in each treatment group.

Table 2: Balanced batch \(\times\) treatment design in the simulation study

Trt1 Trt2
Batch1 10 10
Batch2 10 10 
nitr <- 50
N = 40
p_total = 300
p_trt_relevant = 100 
p_bat_relevant = 200 

# global variance (RDA)
gvar.before <- gvar.clean <- 
  gvar.rbe <- gvar.combat <- 
  gvar.plsdab <- gvar.splsdab <- data.frame(treatment = NA, batch = NA,  
                                            intersection = NA, 
                                            residual = NA)

# individual variance (R2)
r2.trt.before <- r2.trt.clean <- 
  r2.trt.rbe  <- r2.trt.combat <- 
  r2.trt.plsdab <- r2.trt.splsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                       ncol = nitr))
r2.batch.before <- r2.batch.clean <- 
  r2.batch.rbe  <- r2.batch.combat <- 
  r2.batch.plsdab <- r2.batch.splsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                           ncol = nitr))

# precision & recall & F1 (ANOVA)
precision_limma <- recall_limma <- F1_limma <- 
  data.frame(before = NA, clean = NA, 
             rbe = NA, combat = NA, 
             plsda_batch = NA, splsda_batch = NA, 
             sva = NA)

# auc (splsda)
auc_splsda <- 
  data.frame(before = NA, clean = NA, 
             rbe = NA, combat = NA, 
             plsda_batch = NA, splsda_batch = NA)


set.seed(70)
data.cor.res = corStruct(p = 300, zero_prob = 0.7)

for(i in 1: nitr){
  ### initial setup ###
  simulation <- simData_mnegbinom(batch.group = 2,
                                  mean.batch = 7, 
                                  sd.batch = 8, 
                                  mean.trt = 3, 
                                  sd.trt = 2, 
                                  mean.bg = 0, 
                                  sd.bg = 0.2, 
                                  N = 40, 
                                  p_total = 300, 
                                  p_trt_relevant = 100, 
                                  p_bat_relevant = 200, 
                                  percentage_overlap_samples = 0.5, 
                                  percentage_overlap_variables = 0.5, 
                                  data.cor = data.cor.res$data.cor, 
                                  disp = 10, prob_zero = 0, 
                                  seeds = i)
  
  set.seed(i)
  raw_count <- simulation$data
  raw_count_clean <- simulation$cleanData
  
  ## log transformation
  data_log <- log(raw_count + 1)
  data_log_clean <- log(raw_count_clean + 1)
  
  trt <- simulation$Y.trt
  batch <- simulation$Y.bat
  
  true.trt <- simulation$true.trt
  true.batch <- simulation$true.batch
  
  Batch_Trt.factors <- data.frame(Batch = batch, Treatment = trt)
  
  ### Original ###
  X <- data_log
  
  ### Clean data ###
  X.clean <- data_log_clean
  
  #####
  rownames(X) = rownames(X.clean) = names(trt) = names(batch) = 
    paste0('sample', 1:N)
  
  colnames(X) = colnames(X.clean) = paste0('otu', 1:p_total)
  
  ### Before correction ###
  # global variance (RDA)
  rda.before = varpart(scale(X), ~ Treatment, ~ Batch, 
                       data = Batch_Trt.factors)
  gvar.before[i,] <- rda.before$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.before <- lmFit(t(scale(X)), design = model.matrix(~ as.factor(trt)))
  fit.result.before <- topTable(eBayes(fit.before), coef = 2, number = p_total)
  otu.sig.before <- 
    rownames(fit.result.before)[fit.result.before$adj.P.Val <= 0.05]
  
  precision_limma.before <- 
    length(intersect(colnames(X)[true.trt], otu.sig.before))/
    length(otu.sig.before)
  recall_limma.before <- 
    length(intersect(colnames(X)[true.trt], otu.sig.before))/length(true.trt)
  F1_limma.before <- 
    (2*precision_limma.before*recall_limma.before)/
    (precision_limma.before + recall_limma.before)
  
  ## replace NA value with 0
  if(precision_limma.before == 'NaN'){
    precision_limma.before = 0
  }
  if(F1_limma.before == 'NaN'){
    F1_limma.before = 0
  }
  
  # individual variance (R2)
  indiv.trt.before <- c()
  indiv.batch.before <- c()
  for(c in seq_len(ncol(X))){
    fit.res1 <- lm(scale(X)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.before <- c(indiv.trt.before, fit.summary1$r.squared)
    indiv.batch.before <- c(indiv.batch.before, fit.summary2$r.squared)
  }
  r2.trt.before[ ,i] <-  indiv.trt.before
  r2.batch.before[ ,i] <-  indiv.batch.before
  
  
  # auc (sPLSDA)
  fit.before_plsda <- splsda(X = X, Y = trt, ncomp = 1)
  
  true.response <- rep(0, p_total)
  true.response[true.trt] = 1
  before.predictor <- as.numeric(abs(fit.before_plsda$loadings$X))
  roc.before_splsda <- roc(true.response, before.predictor, auc = TRUE)
  auc.before_splsda <- roc.before_splsda$auc
  
  
  ##############################################################################
  ### Ground-truth data ###
  # global variance (RDA)
  rda.clean = varpart(scale(X.clean), ~ Treatment, ~ Batch, 
                      data = Batch_Trt.factors)
  gvar.clean[i, ] <- rda.clean$part$indfract$Adj.R.squared
  
  
  # precision & recall & F1 (ANOVA)
  fit.clean <- lmFit(t(scale(X.clean)), design = model.matrix(~ as.factor(trt)))
  fit.result.clean <- topTable(eBayes(fit.clean), coef = 2, number = p_total)
  otu.sig.clean <- 
    rownames(fit.result.clean)[fit.result.clean$adj.P.Val <= 0.05]
  
  precision_limma.clean<- 
    length(intersect(colnames(X)[true.trt], otu.sig.clean))/
    length(otu.sig.clean)
  recall_limma.clean<- 
    length(intersect(colnames(X)[true.trt], otu.sig.clean))/
    length(true.trt)
  F1_limma.clean <- 
    (2*precision_limma.clean*recall_limma.clean)/
    (precision_limma.clean + recall_limma.clean)
  
  ## replace NA value with 0
  if(precision_limma.clean == 'NaN'){
    precision_limma.clean = 0
  }
  if(F1_limma.clean == 'NaN'){
    F1_limma.clean = 0
  }
  
  # individual variance (R2)
  indiv.trt.clean <- c()
  indiv.batch.clean <- c()
  for(c in seq_len(ncol(X.clean))){
    fit.res1 <- lm(scale(X.clean)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.clean)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.clean <- c(indiv.trt.clean, fit.summary1$r.squared)
    indiv.batch.clean <- c(indiv.batch.clean, fit.summary2$r.squared)
  }
  r2.trt.clean[ ,i] <-  indiv.trt.clean
  r2.batch.clean[ ,i] <-  indiv.batch.clean
  
  # auc (sPLSDA)
  fit.clean_plsda <- splsda(X = X.clean, Y = trt, ncomp = 1)
  
  clean.predictor <- as.numeric(abs(fit.clean_plsda$loadings$X))
  roc.clean_splsda <- roc(true.response, clean.predictor, auc = TRUE)
  auc.clean_splsda <- roc.clean_splsda$auc
  
  ##############################################################################
  ### removeBatchEffect corrected data ###
  X.rbe <-t(removeBatchEffect(t(X), batch = batch, 
                              design = model.matrix(~ as.factor(trt))))
  
  # global variance (RDA)
  rda.rbe = varpart(scale(X.rbe), ~ Treatment, ~ Batch, 
                    data = Batch_Trt.factors)
  gvar.rbe[i, ] <- rda.rbe$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.rbe <- lmFit(t(scale(X.rbe)), 
                   design = model.matrix( ~ as.factor(trt)))
  fit.result.rbe <- topTable(eBayes(fit.rbe), coef = 2, number = p_total)
  otu.sig.rbe <- rownames(fit.result.rbe)[fit.result.rbe$adj.P.Val <= 0.05]
  
  precision_limma.rbe <- length(intersect(colnames(X)[true.trt], otu.sig.rbe))/
    length(otu.sig.rbe)
  recall_limma.rbe <- length(intersect(colnames(X)[true.trt], otu.sig.rbe))/
    length(true.trt)
  F1_limma.rbe <- (2*precision_limma.rbe*recall_limma.rbe)/
    (precision_limma.rbe + recall_limma.rbe)
  
  ## replace NA value with 0
  if(precision_limma.rbe == 'NaN'){
    precision_limma.rbe = 0
  }
  if(F1_limma.rbe == 'NaN'){
    F1_limma.rbe = 0
  }
  
  # individual variance (R2)
  indiv.trt.rbe <- c()
  indiv.batch.rbe <- c()
  for(c in seq_len(ncol(X.rbe))){
    fit.res1 <- lm(scale(X.rbe)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.rbe)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.rbe <- c(indiv.trt.rbe, fit.summary1$r.squared)
    indiv.batch.rbe <- c(indiv.batch.rbe, fit.summary2$r.squared)
  }
  r2.trt.rbe[ ,i] <-  indiv.trt.rbe
  r2.batch.rbe[ ,i] <-  indiv.batch.rbe
  
  
  # auc (sPLSDA)
  fit.rbe_plsda <- splsda(X = X.rbe, Y = trt, ncomp = 1)
  
  rbe.predictor <- as.numeric(abs(fit.rbe_plsda$loadings$X))
  roc.rbe_splsda <- roc(true.response, rbe.predictor, auc = TRUE)
  auc.rbe_splsda <- roc.rbe_splsda$auc
  
  ##############################################################################
  ### ComBat corrected data ###
  X.combat <- t(ComBat(dat = t(X), batch = batch, 
                       mod = model.matrix( ~ as.factor(trt))))
  
  # global variance (RDA)
  rda.combat = varpart(scale(X.combat), ~ Treatment, ~ Batch, 
                       data = Batch_Trt.factors)
  gvar.combat[i, ] <- rda.combat$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.combat <- lmFit(t(scale(X.combat)), 
                      design = model.matrix( ~ as.factor(trt)))
  fit.result.combat <- topTable(eBayes(fit.combat), coef = 2, number = p_total)
  otu.sig.combat <- rownames(fit.result.combat)[fit.result.combat$adj.P.Val <= 
                                                  0.05]
  
  precision_limma.combat <- 
    length(intersect(colnames(X)[true.trt], otu.sig.combat))/
    length(otu.sig.combat)
  recall_limma.combat <- 
    length(intersect(colnames(X)[true.trt], otu.sig.combat))/
    length(true.trt)
  F1_limma.combat <- (2*precision_limma.combat*recall_limma.combat)/
    (precision_limma.combat + recall_limma.combat)
  
  ## replace NA value with 0
  if(precision_limma.combat == 'NaN'){
    precision_limma.combat = 0
  }
  if(F1_limma.combat == 'NaN'){
    F1_limma.combat = 0
  }
  
  # individual variance (R2)
  indiv.trt.combat <- c()
  indiv.batch.combat <- c()
  for(c in seq_len(ncol(X.combat))){
    fit.res1 <- lm(scale(X.combat)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.combat)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.combat <- c(indiv.trt.combat, fit.summary1$r.squared)
    indiv.batch.combat <- c(indiv.batch.combat, fit.summary2$r.squared)
  }
  r2.trt.combat[ ,i] <-  indiv.trt.combat
  r2.batch.combat[ ,i] <-  indiv.batch.combat
  
  
  # auc (sPLSDA)
  fit.combat_plsda <- splsda(X = X.combat, Y = trt, ncomp = 1)
  
  combat.predictor <- as.numeric(abs(fit.combat_plsda$loadings$X))
  roc.combat_splsda <- roc(true.response, combat.predictor, auc = TRUE)
  auc.combat_splsda <- roc.combat_splsda$auc
  
  
  ##############################################################################
  ### PLSDA-batch corrected data ###
  X.plsda_batch.correct <- PLSDA_batch(X = X, 
                                       Y.trt = trt, Y.bat = batch, 
                                       ncomp.trt = 1, ncomp.bat = 1)
  X.plsda_batch <- X.plsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.plsda_batch = varpart(scale(X.plsda_batch), ~ Treatment, ~ Batch, 
                            data = Batch_Trt.factors)
  gvar.plsdab[i, ] <- rda.plsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.plsda_batch <- lmFit(t(scale(X.plsda_batch)), 
                           design = model.matrix( ~ as.factor(trt)))
  fit.result.plsda_batch <- topTable(eBayes(fit.plsda_batch), 
                                     coef = 2, number = p_total)
  otu.sig.plsda_batch <- rownames(fit.result.plsda_batch)[
    fit.result.plsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.plsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.plsda_batch))/
    length(otu.sig.plsda_batch)
  recall_limma.plsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.plsda_batch))/
    length(true.trt)
  F1_limma.plsda_batch <- 
    (2*precision_limma.plsda_batch*recall_limma.plsda_batch)/
    (precision_limma.plsda_batch + recall_limma.plsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.plsda_batch == 'NaN'){
    precision_limma.plsda_batch = 0
  }
  if(F1_limma.plsda_batch == 'NaN'){
    F1_limma.plsda_batch = 0
  }
  
  # individual variance (R2)
  indiv.trt.plsda_batch <- c()
  indiv.batch.plsda_batch <- c()
  for(c in seq_len(ncol(X.plsda_batch))){
    fit.res1 <- lm(scale(X.plsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.plsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.plsda_batch <- c(indiv.trt.plsda_batch, 
                               fit.summary1$r.squared)
    indiv.batch.plsda_batch <- c(indiv.batch.plsda_batch, 
                                 fit.summary2$r.squared)
  }
  r2.trt.plsdab[ ,i] <-  indiv.trt.plsda_batch
  r2.batch.plsdab[ ,i] <-  indiv.batch.plsda_batch
  
  # auc (sPLSDA)
  fit.plsda_batch_plsda <- splsda(X = X.plsda_batch, Y = trt, ncomp = 1)
  
  plsda_batch.predictor <- as.numeric(abs(fit.plsda_batch_plsda$loadings$X))
  roc.plsda_batch_splsda <- roc(true.response, 
                                plsda_batch.predictor, auc = TRUE)
  auc.plsda_batch_splsda <- roc.plsda_batch_splsda$auc
  
  ##############################################################################
  ### sPLSDA-batch corrected data ###
  X.splsda_batch.correct <- PLSDA_batch(X = X, 
                                        Y.trt = trt, 
                                        Y.bat = batch, 
                                        ncomp.trt = 1, 
                                        keepX.trt = length(true.trt), 
                                        ncomp.bat = 1)
  X.splsda_batch <- X.splsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.splsda_batch = varpart(scale(X.splsda_batch), ~ Treatment, ~ Batch, 
                             data = Batch_Trt.factors)
  gvar.splsdab[i, ] <- rda.splsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.splsda_batch <- lmFit(t(scale(X.splsda_batch)), 
                            design = model.matrix( ~ as.factor(trt)))
  fit.result.splsda_batch <- topTable(eBayes(fit.splsda_batch), coef = 2, 
                                      number = p_total)
  otu.sig.splsda_batch <- rownames(fit.result.splsda_batch)[
    fit.result.splsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.splsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.splsda_batch))/
    length(otu.sig.splsda_batch)
  recall_limma.splsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.splsda_batch))/
    length(true.trt)
  F1_limma.splsda_batch <- 
    (2*precision_limma.splsda_batch*recall_limma.splsda_batch)/
    (precision_limma.splsda_batch + recall_limma.splsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.splsda_batch == 'NaN'){
    precision_limma.splsda_batch = 0
  }
  if(F1_limma.splsda_batch == 'NaN'){
    F1_limma.splsda_batch = 0
  }
  
  
  # individual variance (R2)
  indiv.trt.splsda_batch <- c()
  indiv.batch.splsda_batch <- c()
  for(c in seq_len(ncol(X.splsda_batch))){
    fit.res1 <- lm(scale(X.splsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.splsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.splsda_batch <- c(indiv.trt.splsda_batch, 
                                fit.summary1$r.squared)
    indiv.batch.splsda_batch <- c(indiv.batch.splsda_batch, 
                                  fit.summary2$r.squared)
  }
  r2.trt.splsdab[ ,i] <-  indiv.trt.splsda_batch
  r2.batch.splsdab[ ,i] <-  indiv.batch.splsda_batch
  
  # auc (sPLSDA)
  fit.splsda_batch_plsda <- splsda(X = X.splsda_batch, Y = trt, ncomp = 1)
  
  splsda_batch.predictor <- as.numeric(abs(fit.splsda_batch_plsda$loadings$X))
  roc.splsda_batch_splsda <- roc(true.response, 
                                 splsda_batch.predictor, auc = TRUE)
  auc.splsda_batch_splsda <- roc.splsda_batch_splsda$auc
  
  ##############################################################################
  ### SVA ###
  X.mod <- model.matrix(~ as.factor(trt))
  X.mod0 <- model.matrix(~ 1, data = as.factor(trt))
  X.sva.n <- num.sv(dat = t(X), mod = X.mod, method = 'leek')
  X.sva <- sva(t(X), X.mod, X.mod0, n.sv = X.sva.n)
  
  X.mod.batch <- cbind(X.mod, X.sva$sv)
  X.mod0.batch <- cbind(X.mod0, X.sva$sv)
  X.sva.p <- f.pvalue(t(X), X.mod.batch, X.mod0.batch)
  X.sva.p.adj <- p.adjust(X.sva.p, method = 'fdr')
  
  otu.sig.sva <- which(X.sva.p.adj <= 0.05)
  
  # precision & recall & F1 (ANOVA)
  precision_limma.sva <- 
    length(intersect(true.trt, otu.sig.sva))/length(otu.sig.sva)
  recall_limma.sva <- 
    length(intersect(true.trt, otu.sig.sva))/length(true.trt)
  F1_limma.sva <- 
    (2*precision_limma.sva*recall_limma.sva)/
    (precision_limma.sva + recall_limma.sva)
  
  ## replace NA value with 0
  if(precision_limma.sva == 'NaN'){
    precision_limma.sva = 0
  }
  if(F1_limma.sva == 'NaN'){
    F1_limma.sva = 0
  }
  
  
  # summary
  # precision & recall & F1 (ANOVA)
  precision_limma[i, ] <- c(`Before correction` = precision_limma.before, 
                            `Ground-truth data` = precision_limma.clean,
                            `removeBatchEffect` = precision_limma.rbe,
                            ComBat = precision_limma.combat,
                            `PLSDA-batch` = precision_limma.plsda_batch,
                            `sPLSDA-batch` = precision_limma.splsda_batch,
                            SVA = precision_limma.sva)
  
  recall_limma[i, ] <- c(`Before correction` = recall_limma.before, 
                         `Ground-truth data` = recall_limma.clean,
                         `removeBatchEffect` = recall_limma.rbe,
                         ComBat = recall_limma.combat,
                         `PLSDA-batch` = recall_limma.plsda_batch,
                         `sPLSDA-batch` = recall_limma.splsda_batch,
                         SVA = recall_limma.sva)
  
  F1_limma[i, ] <- c(`Before correction` = F1_limma.before, 
                     `Ground-truth data` = F1_limma.clean,
                     `removeBatchEffect` = F1_limma.rbe,
                     ComBat = F1_limma.combat,
                     `PLSDA-batch` = F1_limma.plsda_batch,
                     `sPLSDA-batch` = F1_limma.splsda_batch,
                     SVA = F1_limma.sva)
  
  # auc (splsda)
  auc_splsda[i, ] <- c(`Before correction` = auc.before_splsda, 
                       `Ground-truth data` = auc.clean_splsda, 
                       `removeBatchEffect` = auc.rbe_splsda, 
                       ComBat = auc.combat_splsda, 
                       `PLSDA-batch` = auc.plsda_batch_splsda, 
                       `sPLSDA-batch` = auc.splsda_batch_splsda)
  
  # print(i)
  
}

4.2.2 Figures

# global variance (RDA)
prop.gvar.all <- rbind(`Before correction` = colMeans(gvar.before),
                       `Ground-truth data` = colMeans(gvar.clean),
                       removeBatchEffect = colMeans(gvar.rbe),
                       ComBat = colMeans(gvar.combat),
                       `PLSDA-batch` = colMeans(gvar.plsdab),
                       `sPLSDA-batch` = colMeans(gvar.splsdab))

prop.gvar.all[prop.gvar.all < 0] = 0
prop.gvar.all <- t(apply(prop.gvar.all, 1, function(x){x/sum(x)}))
colnames(prop.gvar.all) <- c('Treatment', 'Intersection', 'Batch', 'Residuals')

partVar_plot(prop.df = prop.gvar.all)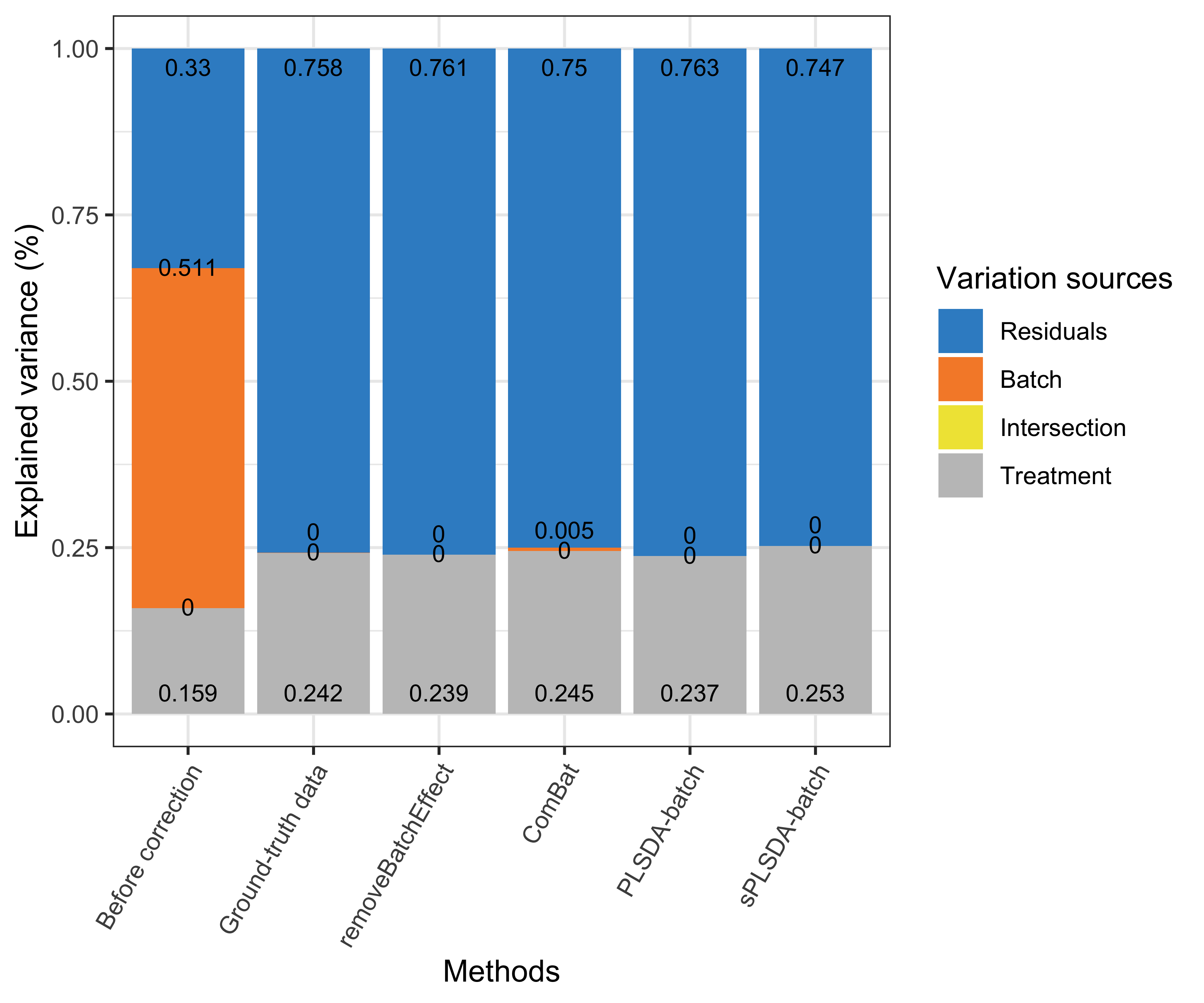
Figure 1: Simulation studies (two batch groups): comparison of explained variance before and after batch effect correction for the balanced batch × treatment design.

Figure 4.1: Figure 1: Simulation studies (two batch groups): comparison of explained variance before and after batch effect correction for the balanced batch × treatment design.

Efficient batch effect correction methods should generate data with a null proportion of variance explained by batch effects, and a proportion of variance explained by treatment that is larger compared to the original data, as shown in the figure above original data and ground-truth data.

For a balanced batch \(\times\) treatment design, we observed no intersection shared between treatment and batch variance, as expected. All methods successfully removed batch variance and preserved (or slightly increased) treatment variance (sPLSDA-batch), with the exception of ComBat where a very small amount of batch variance remained.

################################################################################
# individual variance (R2)
## boxplot
# class
gclass <- c(rep('Treatment only', p_trt_relevant), 
            rep('Batch only', (p_total - p_trt_relevant)))
gclass[intersect(true.trt, true.batch)] = 'Treatment & batch'
gclass[setdiff(1:p_total, union(true.trt, true.batch))] = 'No effect'

gclass <- factor(gclass, levels = c('Treatment & batch', 
                                    'Treatment only', 
                                    'Batch only', 
                                    'No effect'))

before.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.before), 
                                      rowMeans(r2.batch.before)), 
                               type = as.factor(rep(c('Treatment','Batch'), 
                                                    each = 300)),
                               class = rep(gclass,2))
clean.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.clean), 
                                     rowMeans(r2.batch.clean)), 
                              type = as.factor(rep(c('Treatment','Batch'), 
                                                   each = 300)),
                              class = rep(gclass,2))
rbe.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.rbe), 
                                   rowMeans(r2.batch.rbe)), 
                            type = as.factor(rep(c('Treatment','Batch'), 
                                                 each = 300)),
                            class = rep(gclass,2))
combat.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.combat), 
                                      rowMeans(r2.batch.combat)), 
                               type = as.factor(rep(c('Treatment','Batch'), 
                                                    each = 300)),
                               class = rep(gclass,2))
plsda_batch.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.plsdab), 
                                           rowMeans(r2.batch.plsdab)), 
                                    type = as.factor(rep(c('Treatment','Batch'), 
                                                         each = 300)),
                                    class = rep(gclass,2))
splsda_batch.r2.df.ggp <- 
  data.frame(r2 = c(rowMeans(r2.trt.splsdab), 
                    rowMeans(r2.batch.splsdab)), 
             type = as.factor(rep(c('Treatment','Batch'), 
                                  each = 300)),
             class = rep(gclass,2))

all.r2.df.ggp <- rbind(before.r2.df.ggp, clean.r2.df.ggp,
                       rbe.r2.df.ggp, combat.r2.df.ggp,
                       plsda_batch.r2.df.ggp, splsda_batch.r2.df.ggp)

all.r2.df.ggp$methods <- rep(c('Before correction', 
                               'Ground-truth data', 
                               'removeBatchEffect', 
                               'ComBat',
                               'PLSDA-batch', 
                               'sPLSDA-batch'), each = 600)

all.r2.df.ggp$methods <- factor(all.r2.df.ggp$methods, 
                                levels = unique(all.r2.df.ggp$methods))

ggplot(all.r2.df.ggp, aes(x = type, y = r2, fill = class)) +
  geom_boxplot(alpha = 0.80) +
  theme_bw() + 
  theme(text = element_text(size = 18),
        axis.title.x = element_blank(),
        axis.title.y = element_blank(),
        panel.grid.minor.x = element_blank(),
        panel.grid.major.x = element_blank(),
        legend.position = "right") + facet_grid(class ~ methods) + 
  scale_fill_manual(values=c('dark gray', color.mixo(4), 
                             color.mixo(5), color.mixo(9)))
Figure 2: Simulation studies (two batch groups): R2 values for each microbial variable before and after batch effect correction for the balanced batch × treatment design.

Figure 4.2: Figure 2: Simulation studies (two batch groups): R2 values for each microbial variable before and after batch effect correction for the balanced batch × treatment design. 

################################################################################
## barplot
# class
before.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.before), gclass, sum), 
                    tapply(rowMeans(r2.batch.before), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

clean.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.clean), gclass, sum), 
                    tapply(rowMeans(r2.batch.clean), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

rbe.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.rbe), gclass, sum), 
                    tapply(rowMeans(r2.batch.rbe), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

combat.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.combat), gclass, sum), 
                    tapply(rowMeans(r2.batch.combat), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

plsda_batch.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.plsdab), gclass, sum), 
                    tapply(rowMeans(r2.batch.plsdab), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

splsda_batch.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.splsdab), gclass, sum), 
                    tapply(rowMeans(r2.batch.splsdab), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))


all.r2.df.bp <- rbind(before.r2.df.bp, clean.r2.df.bp,
                      rbe.r2.df.bp, combat.r2.df.bp,
                      plsda_batch.r2.df.bp, splsda_batch.r2.df.bp)


all.r2.df.bp$methods <- rep(c('Before correction', 
                              'Ground-truth data', 
                              'removeBatchEffect', 'ComBat',
                              'PLSDA-batch', 'sPLSDA-batch'), each = 8)

all.r2.df.bp$methods <- factor(all.r2.df.bp$methods, 
                               levels = unique(all.r2.df.bp$methods))

ggplot(all.r2.df.bp, aes(x = type, y = r2, fill = class)) +
  geom_bar(stat="identity") + 
  theme_bw() + 
  theme(text = element_text(size = 18),
        axis.title.x = element_blank(),
        axis.title.y = element_blank(),
        panel.grid.minor.x = element_blank(),
        panel.grid.major.x = element_blank(),
        legend.position = "right") + facet_grid(class ~ methods) + 
  scale_fill_manual(values=c('dark gray', color.mixo(4), 
                             color.mixo(5), color.mixo(9)))
Figure 3: Simulation studies (two batch groups): the sum of R2 values for each microbial variable before and after batch effect correction for the balanced batch × treatment design.

Figure 4.3: Figure 3: Simulation studies (two batch groups): the sum of R2 values for each microbial variable before and after batch effect correction for the balanced batch × treatment design.

We estimated the proportion of variance explained by treatment and batch effects for each variable using the \(R^2\) value. removeBatchEffect and PLSDA-batch had the best performance, with results very similar to the ground-truth data. ComBat retained more batch variance of variables with batch effects only, and with both batch and treatment effects, indicating an incomplete removal of batch effects. This result is in agreement with the overall pRDA evaluation described earlier. For sPLSDA-batch, variables with no treatment effect (batch effects only) included a slight amount of (spurious) treatment variance. This was also observed in pRDA evaluation. However, sPLSDA-batch performed as well as PLSDA-batch when the simulated data did not include variables with both batch and treatment effects.

# precision & recall & F1 (ANOVA & sPLSDA)
## mean
acc_mean <- rbind(colMeans(precision_limma), colMeans(recall_limma), 
                  colMeans(F1_limma), c(colMeans(auc_splsda), sva = NA))
rownames(acc_mean) <- c('Precision', 'Recall', 'F1', 'AUC')
colnames(acc_mean) <- c('Before correction', 'Ground-truth data', 
                        'removeBatchEffect', 'ComBat', 
                        'PLSDA-batch', 'sPLSDA-batch', 'SVA')
acc_mean <- format(acc_mean, digits = 3)
knitr::kable(acc_mean, caption = 'Table 3: Simulation studies (two batch groups): summary of accuracy measurements before and after batch effect correction for the balanced batch × treatment design (mean).')
Table 4.1: Table 3: Simulation studies (two batch groups): summary of accuracy measurements before and after batch effect correction for the balanced batch × treatment design (mean).
Before correction Ground-truth data removeBatchEffect ComBat PLSDA-batch sPLSDA-batch SVA
Precision 0.984 0.952 0.950 0.952 0.952 0.807 0.957
Recall 0.674 0.900 0.910 0.911 0.910 0.910 0.934
F1 0.799 0.923 0.927 0.929 0.929 0.851 0.944
AUC 0.944 0.964 0.968 0.968 0.969 0.954 NA

The results from the accuracy measures combined with variable selection highlight the importance of removing batch effects as both F1 score and AUC largely improved compared to the original data.

Starting from the original data compared to the ground-truth data, selected variables had a higher precision, lower recall and lower AUC, indicating a smaller number of variables selected with an actual treatment effect. Combined with univariate one-way ANOVA, SVA performed best with the highest, and sometimes greater, accuracy measurements than the ground-truth data. The other methods led to similar performance with the exception of sPLSDA-batch, which selected more false positives than the other methods. PLSDA-batch led to a slightly better AUC than the other methods.

## sd
acc_sd <- rbind(apply(precision_limma, 2, sd), apply(recall_limma, 2, sd), 
                apply(F1_limma, 2, sd), c(apply(auc_splsda, 2, sd), NA))
rownames(acc_sd) <- c('Precision', 'Recall', 'F1', 'AUC')
colnames(acc_sd) <- c('Before correction', 'Ground-truth data', 
                      'removeBatchEffect', 'ComBat', 
                      'PLSDA-batch', 'sPLSDA-batch', 'SVA')
acc_sd <- format(acc_sd, digits = 1)
knitr::kable(acc_sd, caption = 'Table 4: Simulation studies (two batch groups): summary of accuracy measurements before and after batch effect correction for the balanced batch × treatment design (standard deviation).')
Table 4.2: Table 4: Simulation studies (two batch groups): summary of accuracy measurements before and after batch effect correction for the balanced batch × treatment design (standard deviation).
Before correction Ground-truth data removeBatchEffect ComBat PLSDA-batch sPLSDA-batch SVA
Precision 0.04 0.08 0.09 0.08 0.08 0.11 0.06
Recall 0.03 0.03 0.03 0.03 0.03 0.03 0.03
F1 0.02 0.05 0.05 0.05 0.05 0.06 0.04
AUC 0.02 0.02 0.02 0.02 0.01 0.02 NA

4.2.3 Unbalanced batch \(\times\) treatment design

The unbalanced design included 4 and 16 samples from batch1 and batch2 respectively in trt1, 16 and 4 samples from batch1 and batch2 in trt2.

Table 5: Unbalanced batch \(\times\) treatment design in the simulation study

Trt1 Trt2
Batch1 4 16
Batch2 16 4 
nitr <- 50
N = 40
p_total = 300
p_trt_relevant = 100 
p_bat_relevant = 200 

# global variance (RDA)
gvar.before <- gvar.clean <- 
  gvar.rbe <- gvar.combat <- 
  gvar.wplsdab <- gvar.swplsdab <- 
  gvar.plsdab <- gvar.splsdab <- data.frame(treatment = NA, batch = NA,  
                                            intersection = NA, 
                                            residual = NA)

# individual variance (R2)
r2.trt.before <- r2.trt.clean <- 
  r2.trt.rbe  <- r2.trt.combat <- 
  r2.trt.wplsdab <- r2.trt.swplsdab <-
  r2.trt.plsdab <- r2.trt.splsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                       ncol = nitr))
r2.batch.before <- r2.batch.clean <- 
  r2.batch.rbe  <- r2.batch.combat <- 
  r2.batch.wplsdab <- r2.batch.swplsdab <-
  r2.batch.plsdab <- r2.batch.splsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                           ncol = nitr))

# precision & recall & F1 (ANOVA)
precision_limma <- recall_limma <- F1_limma <- 
  data.frame(before = NA, clean = NA, 
             rbe = NA, combat = NA, 
             wplsda_batch = NA, swplsda_batch = NA, 
             sva = NA)

# auc (splsda)
auc_splsda <- 
  data.frame(before = NA, clean = NA, 
             rbe = NA, combat = NA, 
             wplsda_batch = NA, swplsda_batch = NA)


set.seed(70)
data.cor.res = corStruct(p = 300, zero_prob = 0.7)

for(i in 1: nitr){
  ### initial setup ###
  simulation <- simData_mnegbinom(batch.group = 2,
                                  mean.batch = 7, 
                                  sd.batch = 8, 
                                  mean.trt = 3, 
                                  sd.trt = 2, 
                                  mean.bg = 0, 
                                  sd.bg = 0.2, 
                                  N = 40, 
                                  p_total = 300, 
                                  p_trt_relevant = 100, 
                                  p_bat_relevant = 200, 
                                  percentage_overlap_samples = 0.2, 
                                  percentage_overlap_variables = 0.5, 
                                  data.cor = data.cor.res$data.cor, 
                                  disp = 10, prob_zero = 0, 
                                  seeds = i)
  
  set.seed(i)
  raw_count <- simulation$data
  raw_count_clean <- simulation$cleanData
  
  ## log transformation
  data_log <- log(raw_count + 1)
  data_log_clean <- log(raw_count_clean + 1)
  
  trt <- simulation$Y.trt
  batch <- simulation$Y.bat
  
  true.trt <- simulation$true.trt
  true.batch <- simulation$true.batch
  
  Batch_Trt.factors <- data.frame(Batch = batch, Treatment = trt)
  
  ### Original ###
  X <- data_log
  
  ### Clean data ###
  X.clean <- data_log_clean
  
  #####
  rownames(X) = rownames(X.clean) = names(trt) = names(batch) = 
    paste0('sample', 1:N)
  
  colnames(X) = colnames(X.clean) = paste0('otu', 1:p_total)
  
  ### Before correction ###
  # global variance (RDA)
  rda.before = varpart(scale(X), ~ Treatment, ~ Batch, 
                       data = Batch_Trt.factors)
  gvar.before[i,] <- rda.before$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.before <- lmFit(t(scale(X)), design = model.matrix(~ as.factor(trt)))
  fit.result.before <- topTable(eBayes(fit.before), coef = 2, number = p_total)
  otu.sig.before <- 
    rownames(fit.result.before)[fit.result.before$adj.P.Val <= 0.05]
  
  precision_limma.before <- 
    length(intersect(colnames(X)[true.trt], otu.sig.before))/
    length(otu.sig.before)
  recall_limma.before <- 
    length(intersect(colnames(X)[true.trt], otu.sig.before))/
    length(true.trt)
  F1_limma.before <- 
    (2*precision_limma.before*recall_limma.before)/
    (precision_limma.before + recall_limma.before)
  
  ## replace NA value with 0
  if(precision_limma.before == 'NaN'){
    precision_limma.before = 0
  }
  if(F1_limma.before == 'NaN'){
    F1_limma.before = 0
  }
  
  # individual variance (R2)
  indiv.trt.before <- c()
  indiv.batch.before <- c()
  for(c in seq_len(ncol(X))){
    fit.res1 <- lm(scale(X)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.before <- c(indiv.trt.before, fit.summary1$r.squared)
    indiv.batch.before <- c(indiv.batch.before, fit.summary2$r.squared)
  }
  r2.trt.before[ ,i] <-  indiv.trt.before
  r2.batch.before[ ,i] <-  indiv.batch.before
  
  
  # auc (sPLSDA)
  fit.before_plsda <- splsda(X = X, Y = trt, ncomp = 1)
  
  true.response <- rep(0, p_total)
  true.response[true.trt] = 1
  before.predictor <- as.numeric(abs(fit.before_plsda$loadings$X))
  roc.before_splsda <- roc(true.response, before.predictor, auc = TRUE)
  auc.before_splsda <- roc.before_splsda$auc
  
  
  ##############################################################################
  ### Ground-truth data ###
  # global variance (RDA)
  rda.clean = varpart(scale(X.clean), ~ Treatment, ~ Batch, 
                      data = Batch_Trt.factors)
  gvar.clean[i, ] <- rda.clean$part$indfract$Adj.R.squared
  
  
  # precision & recall & F1 (ANOVA)
  fit.clean <- lmFit(t(scale(X.clean)), design = model.matrix(~ as.factor(trt)))
  fit.result.clean <- topTable(eBayes(fit.clean), coef = 2, number = p_total)
  otu.sig.clean <- 
    rownames(fit.result.clean)[fit.result.clean$adj.P.Val <= 0.05]
  
  precision_limma.clean <- 
    length(intersect(colnames(X)[true.trt], otu.sig.clean))/
    length(otu.sig.clean)
  recall_limma.clean <- 
    length(intersect(colnames(X)[true.trt], otu.sig.clean))/length(true.trt)
  F1_limma.clean <- 
    (2*precision_limma.clean*recall_limma.clean)/
    (precision_limma.clean + recall_limma.clean)
  
  ## replace NA value with 0
  if(precision_limma.clean == 'NaN'){
    precision_limma.clean = 0
  }
  if(F1_limma.clean == 'NaN'){
    F1_limma.clean = 0
  }
  
  # individual variance (R2)
  indiv.trt.clean <- c()
  indiv.batch.clean <- c()
  for(c in seq_len(ncol(X.clean))){
    fit.res1 <- lm(scale(X.clean)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.clean)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.clean <- c(indiv.trt.clean, fit.summary1$r.squared)
    indiv.batch.clean <- c(indiv.batch.clean, fit.summary2$r.squared)
  }
  r2.trt.clean[ ,i] <-  indiv.trt.clean
  r2.batch.clean[ ,i] <-  indiv.batch.clean
  
  # auc (sPLSDA)
  fit.clean_plsda <- splsda(X = X.clean, Y = trt, ncomp = 1)
  
  clean.predictor <- as.numeric(abs(fit.clean_plsda$loadings$X))
  roc.clean_splsda <- roc(true.response, clean.predictor, auc = TRUE)
  auc.clean_splsda <- roc.clean_splsda$auc
  
  ##############################################################################
  ### removeBatchEffect corrected data ###
  X.rbe <-t(removeBatchEffect(t(X), batch = batch, 
                              design = model.matrix(~ as.factor(trt))))
  
  # global variance (RDA)
  rda.rbe = varpart(scale(X.rbe), ~ Treatment, ~ Batch, 
                    data = Batch_Trt.factors)
  gvar.rbe[i, ] <- rda.rbe$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.rbe <- lmFit(t(scale(X.rbe)), 
                   design = model.matrix( ~ as.factor(trt)))
  fit.result.rbe <- topTable(eBayes(fit.rbe), coef = 2, number = p_total)
  otu.sig.rbe <- rownames(fit.result.rbe)[fit.result.rbe$adj.P.Val <= 0.05]
  
  precision_limma.rbe <- length(intersect(colnames(X)[true.trt], otu.sig.rbe))/
    length(otu.sig.rbe)
  recall_limma.rbe <- length(intersect(colnames(X)[true.trt], otu.sig.rbe))/
    length(true.trt)
  F1_limma.rbe <- (2*precision_limma.rbe*recall_limma.rbe)/
    (precision_limma.rbe + recall_limma.rbe)
  
  ## replace NA value with 0
  if(precision_limma.rbe == 'NaN'){
    precision_limma.rbe = 0
  }
  if(F1_limma.rbe == 'NaN'){
    F1_limma.rbe = 0
  }
  
  # individual variance (R2)
  indiv.trt.rbe <- c()
  indiv.batch.rbe <- c()
  for(c in seq_len(ncol(X.rbe))){
    fit.res1 <- lm(scale(X.rbe)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.rbe)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.rbe <- c(indiv.trt.rbe, fit.summary1$r.squared)
    indiv.batch.rbe <- c(indiv.batch.rbe, fit.summary2$r.squared)
  }
  r2.trt.rbe[ ,i] <-  indiv.trt.rbe
  r2.batch.rbe[ ,i] <-  indiv.batch.rbe
  
  
  # auc (sPLSDA)
  fit.rbe_plsda <- splsda(X = X.rbe, Y = trt, ncomp = 1)
  
  rbe.predictor <- as.numeric(abs(fit.rbe_plsda$loadings$X))
  roc.rbe_splsda <- roc(true.response, rbe.predictor, auc = TRUE)
  auc.rbe_splsda <- roc.rbe_splsda$auc
  
  ##############################################################################
  ### ComBat corrected data ###
  X.combat <- t(ComBat(dat = t(X), batch = batch, 
                       mod = model.matrix( ~ as.factor(trt))))
  
  # global variance (RDA)
  rda.combat = varpart(scale(X.combat), ~ Treatment, ~ Batch, 
                       data = Batch_Trt.factors)
  gvar.combat[i, ] <- rda.combat$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.combat <- lmFit(t(scale(X.combat)), 
                      design = model.matrix( ~ as.factor(trt)))
  fit.result.combat <- topTable(eBayes(fit.combat), coef = 2, number = p_total)
  otu.sig.combat <- 
    rownames(fit.result.combat)[fit.result.combat$adj.P.Val <= 0.05]
  
  precision_limma.combat <- 
    length(intersect(colnames(X)[true.trt], otu.sig.combat))/
    length(otu.sig.combat)
  recall_limma.combat <- 
    length(intersect(colnames(X)[true.trt], otu.sig.combat))/
    length(true.trt)
  F1_limma.combat <- (2*precision_limma.combat*recall_limma.combat)/
    (precision_limma.combat + recall_limma.combat)
  
  ## replace NA value with 0
  if(precision_limma.combat == 'NaN'){
    precision_limma.combat = 0
  }
  if(F1_limma.combat == 'NaN'){
    F1_limma.combat = 0
  }
  
  # individual variance (R2)
  indiv.trt.combat <- c()
  indiv.batch.combat <- c()
  for(c in seq_len(ncol(X.combat))){
    fit.res1 <- lm(scale(X.combat)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.combat)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.combat <- c(indiv.trt.combat, fit.summary1$r.squared)
    indiv.batch.combat <- c(indiv.batch.combat, fit.summary2$r.squared)
  }
  r2.trt.combat[ ,i] <-  indiv.trt.combat
  r2.batch.combat[ ,i] <-  indiv.batch.combat
  
  
  # auc (sPLSDA)
  fit.combat_plsda <- splsda(X = X.combat, Y = trt, ncomp = 1)
  
  combat.predictor <- as.numeric(abs(fit.combat_plsda$loadings$X))
  roc.combat_splsda <- roc(true.response, combat.predictor, auc = TRUE)
  auc.combat_splsda <- roc.combat_splsda$auc
  
  
  ##############################################################################
  ### wPLSDA-batch corrected data ###
  X.wplsda_batch.correct <- PLSDA_batch(X = X, 
                                        Y.trt = trt, Y.bat = batch, 
                                        ncomp.trt = 1, ncomp.bat = 1,
                                        balance = FALSE)
  X.wplsda_batch <- X.wplsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.wplsda_batch = varpart(scale(X.wplsda_batch), ~ Treatment, ~ Batch, 
                             data = Batch_Trt.factors)
  gvar.wplsdab[i, ] <- rda.wplsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.wplsda_batch <- lmFit(t(scale(X.wplsda_batch)), 
                            design = model.matrix( ~ as.factor(trt)))
  fit.result.wplsda_batch <- topTable(eBayes(fit.wplsda_batch), 
                                      coef = 2, number = p_total)
  otu.sig.wplsda_batch <- rownames(fit.result.wplsda_batch)[
    fit.result.wplsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.wplsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.wplsda_batch))/
    length(otu.sig.wplsda_batch)
  recall_limma.wplsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.wplsda_batch))/
    length(true.trt)
  F1_limma.wplsda_batch <- 
    (2*precision_limma.wplsda_batch*recall_limma.wplsda_batch)/
    (precision_limma.wplsda_batch + recall_limma.wplsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.wplsda_batch == 'NaN'){
    precision_limma.wplsda_batch = 0
  }
  if(F1_limma.wplsda_batch == 'NaN'){
    F1_limma.wplsda_batch = 0
  }
  
  # individual variance (R2)
  indiv.trt.wplsda_batch <- c()
  indiv.batch.wplsda_batch <- c()
  for(c in seq_len(ncol(X.wplsda_batch))){
    fit.res1 <- lm(scale(X.wplsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.wplsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.wplsda_batch <- c(indiv.trt.wplsda_batch, 
                                fit.summary1$r.squared)
    indiv.batch.wplsda_batch <- c(indiv.batch.wplsda_batch, 
                                  fit.summary2$r.squared)
  }
  r2.trt.wplsdab[ ,i] <-  indiv.trt.wplsda_batch
  r2.batch.wplsdab[ ,i] <-  indiv.batch.wplsda_batch
  
  # auc (sPLSDA)
  fit.wplsda_batch_plsda <- splsda(X = X.wplsda_batch, Y = trt, ncomp = 1)
  
  wplsda_batch.predictor <- as.numeric(abs(fit.wplsda_batch_plsda$loadings$X))
  roc.wplsda_batch_splsda <- roc(true.response, 
                                 wplsda_batch.predictor, auc = TRUE)
  auc.wplsda_batch_splsda <- roc.wplsda_batch_splsda$auc
  
  ##############################################################################
  ### sPLSDA-batch corrected data ###
  X.swplsda_batch.correct <- PLSDA_batch(X = X, 
                                         Y.trt = trt, 
                                         Y.bat = batch, 
                                         ncomp.trt = 1, 
                                         keepX.trt = length(true.trt), 
                                         ncomp.bat = 1,
                                         balance = FALSE)
  X.swplsda_batch <- X.swplsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.swplsda_batch = varpart(scale(X.swplsda_batch), ~ Treatment, ~ Batch, 
                              data = Batch_Trt.factors)
  gvar.swplsdab[i, ] <- rda.swplsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.swplsda_batch <- lmFit(t(scale(X.swplsda_batch)), 
                             design = model.matrix( ~ as.factor(trt)))
  fit.result.swplsda_batch <- topTable(eBayes(fit.swplsda_batch), coef = 2, 
                                       number = p_total)
  otu.sig.swplsda_batch <- rownames(fit.result.swplsda_batch)[
    fit.result.swplsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.swplsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.swplsda_batch))/
    length(otu.sig.swplsda_batch)
  recall_limma.swplsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.swplsda_batch))/
    length(true.trt)
  F1_limma.swplsda_batch <- 
    (2*precision_limma.swplsda_batch*recall_limma.swplsda_batch)/
    (precision_limma.swplsda_batch + recall_limma.swplsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.swplsda_batch == 'NaN'){
    precision_limma.swplsda_batch = 0
  }
  if(F1_limma.swplsda_batch == 'NaN'){
    F1_limma.swplsda_batch = 0
  }
  
  
  # individual variance (R2)
  indiv.trt.swplsda_batch <- c()
  indiv.batch.swplsda_batch <- c()
  for(c in seq_len(ncol(X.swplsda_batch))){
    fit.res1 <- lm(scale(X.swplsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.swplsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.swplsda_batch <- c(indiv.trt.swplsda_batch, 
                                 fit.summary1$r.squared)
    indiv.batch.swplsda_batch <- c(indiv.batch.swplsda_batch, 
                                   fit.summary2$r.squared)
  }
  r2.trt.swplsdab[ ,i] <-  indiv.trt.swplsda_batch
  r2.batch.swplsdab[ ,i] <-  indiv.batch.swplsda_batch
  
  # auc (sPLSDA)
  fit.swplsda_batch_plsda <- splsda(X = X.swplsda_batch, Y = trt, ncomp = 1)
  
  swplsda_batch.predictor <- as.numeric(abs(fit.swplsda_batch_plsda$loadings$X))
  roc.swplsda_batch_splsda <- roc(true.response, 
                                  swplsda_batch.predictor, auc = TRUE)
  auc.swplsda_batch_splsda <- roc.swplsda_batch_splsda$auc
  
  ##############################################################################
  ### PLSDA-batch corrected data ###
  X.plsda_batch.correct <- PLSDA_batch(X = X, 
                                       Y.trt = trt, Y.bat = batch, 
                                       ncomp.trt = 1, ncomp.bat = 1)
  X.plsda_batch <- X.plsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.plsda_batch = varpart(scale(X.plsda_batch), ~ Treatment, ~ Batch, 
                            data = Batch_Trt.factors)
  gvar.plsdab[i, ] <- rda.plsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.plsda_batch <- lmFit(t(scale(X.plsda_batch)), 
                           design = model.matrix( ~ as.factor(trt)))
  fit.result.plsda_batch <- topTable(eBayes(fit.plsda_batch), 
                                     coef = 2, number = p_total)
  otu.sig.plsda_batch <- rownames(fit.result.plsda_batch)[
    fit.result.plsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.plsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.plsda_batch))/
    length(otu.sig.plsda_batch)
  recall_limma.plsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.plsda_batch))/
    length(true.trt)
  F1_limma.plsda_batch <- 
    (2*precision_limma.plsda_batch*recall_limma.plsda_batch)/
    (precision_limma.plsda_batch + recall_limma.plsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.plsda_batch == 'NaN'){
    precision_limma.plsda_batch = 0
  }
  if(F1_limma.plsda_batch == 'NaN'){
    F1_limma.plsda_batch = 0
  }
  
  # individual variance (R2)
  indiv.trt.plsda_batch <- c()
  indiv.batch.plsda_batch <- c()
  for(c in seq_len(ncol(X.plsda_batch))){
    fit.res1 <- lm(scale(X.plsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.plsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.plsda_batch <- c(indiv.trt.plsda_batch, 
                               fit.summary1$r.squared)
    indiv.batch.plsda_batch <- c(indiv.batch.plsda_batch, 
                                 fit.summary2$r.squared)
  }
  r2.trt.plsdab[ ,i] <-  indiv.trt.plsda_batch
  r2.batch.plsdab[ ,i] <-  indiv.batch.plsda_batch
  
  # auc (sPLSDA)
  fit.plsda_batch_plsda <- splsda(X = X.plsda_batch, Y = trt, ncomp = 1)
  
  plsda_batch.predictor <- as.numeric(abs(fit.plsda_batch_plsda$loadings$X))
  roc.plsda_batch_splsda <- roc(true.response, 
                                plsda_batch.predictor, auc = TRUE)
  auc.plsda_batch_splsda <- roc.plsda_batch_splsda$auc
  
  ##############################################################################
  ### sPLSDA-batch corrected data ###
  X.splsda_batch.correct <- PLSDA_batch(X = X, 
                                        Y.trt = trt, 
                                        Y.bat = batch, 
                                        ncomp.trt = 1, 
                                        keepX.trt = length(true.trt), 
                                        ncomp.bat = 1)
  X.splsda_batch <- X.splsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.splsda_batch = varpart(scale(X.splsda_batch), ~ Treatment, ~ Batch, 
                             data = Batch_Trt.factors)
  gvar.splsdab[i, ] <- rda.splsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.splsda_batch <- lmFit(t(scale(X.splsda_batch)), 
                            design = model.matrix( ~ as.factor(trt)))
  fit.result.splsda_batch <- topTable(eBayes(fit.splsda_batch), coef = 2, 
                                      number = p_total)
  otu.sig.splsda_batch <- rownames(fit.result.splsda_batch)[
    fit.result.splsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.splsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.splsda_batch))/
    length(otu.sig.splsda_batch)
  recall_limma.splsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.splsda_batch))/
    length(true.trt)
  F1_limma.splsda_batch <- 
    (2*precision_limma.splsda_batch*recall_limma.splsda_batch)/
    (precision_limma.splsda_batch + recall_limma.splsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.splsda_batch == 'NaN'){
    precision_limma.splsda_batch = 0
  }
  if(F1_limma.splsda_batch == 'NaN'){
    F1_limma.splsda_batch = 0
  }
  
  
  # individual variance (R2)
  indiv.trt.splsda_batch <- c()
  indiv.batch.splsda_batch <- c()
  for(c in seq_len(ncol(X.splsda_batch))){
    fit.res1 <- lm(scale(X.splsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.splsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.splsda_batch <- c(indiv.trt.splsda_batch, 
                                fit.summary1$r.squared)
    indiv.batch.splsda_batch <- c(indiv.batch.splsda_batch, 
                                  fit.summary2$r.squared)
  }
  r2.trt.splsdab[ ,i] <-  indiv.trt.splsda_batch
  r2.batch.splsdab[ ,i] <-  indiv.batch.splsda_batch
  
  # auc (sPLSDA)
  fit.splsda_batch_plsda <- splsda(X = X.splsda_batch, Y = trt, ncomp = 1)
  
  splsda_batch.predictor <- as.numeric(abs(fit.splsda_batch_plsda$loadings$X))
  roc.splsda_batch_splsda <- roc(true.response, 
                                 splsda_batch.predictor, auc = TRUE)
  auc.splsda_batch_splsda <- roc.splsda_batch_splsda$auc
  
  ##############################################################################
  ### SVA ###
  X.mod <- model.matrix(~ as.factor(trt))
  X.mod0 <- model.matrix(~ 1, data = as.factor(trt))
  X.sva.n <- num.sv(dat = t(X), mod = X.mod, method = 'leek')
  X.sva <- sva(t(X), X.mod, X.mod0, n.sv = X.sva.n)
  
  X.mod.batch <- cbind(X.mod, X.sva$sv)
  X.mod0.batch <- cbind(X.mod0, X.sva$sv)
  X.sva.p <- f.pvalue(t(X), X.mod.batch, X.mod0.batch)
  X.sva.p.adj <- p.adjust(X.sva.p, method = 'fdr')
  
  otu.sig.sva <- which(X.sva.p.adj <= 0.05)
  
  # precision & recall & F1 (ANOVA)
  precision_limma.sva <- 
    length(intersect(true.trt, otu.sig.sva))/length(otu.sig.sva)
  recall_limma.sva <- 
    length(intersect(true.trt, otu.sig.sva))/length(true.trt)
  F1_limma.sva <- 
    (2*precision_limma.sva*recall_limma.sva)/
    (precision_limma.sva + recall_limma.sva)
  
  ## replace NA value with 0
  if(precision_limma.sva == 'NaN'){
    precision_limma.sva = 0
  }
  if(F1_limma.sva == 'NaN'){
    F1_limma.sva = 0
  }
  
  
  # summary
  # precision & recall & F1 (ANOVA)
  precision_limma[i, ] <- c(`Before correction` = precision_limma.before, 
                            `Ground-truth data` = precision_limma.clean,
                            `removeBatchEffect` = precision_limma.rbe,
                            ComBat = precision_limma.combat,
                            `wPLSDA-batch` = precision_limma.wplsda_batch,
                            `swPLSDA-batch` = precision_limma.swplsda_batch,
                            SVA = precision_limma.sva)
  
  recall_limma[i, ] <- c(`Before correction` = recall_limma.before, 
                         `Ground-truth data` = recall_limma.clean,
                         `removeBatchEffect` = recall_limma.rbe,
                         ComBat = recall_limma.combat,
                         `wPLSDA-batch` = recall_limma.wplsda_batch,
                         `swPLSDA-batch` = recall_limma.swplsda_batch,
                         SVA = recall_limma.sva)
  
  F1_limma[i, ] <- c(`Before correction` = F1_limma.before, 
                     `Ground-truth data` = F1_limma.clean,
                     `removeBatchEffect` = F1_limma.rbe,
                     ComBat = F1_limma.combat,
                     `wPLSDA-batch` = F1_limma.wplsda_batch,
                     `swPLSDA-batch` = F1_limma.swplsda_batch,
                     SVA = F1_limma.sva)
  
  # auc (splsda)
  auc_splsda[i, ] <- c(`Before correction` = auc.before_splsda, 
                       `Ground-truth data` = auc.clean_splsda, 
                       `removeBatchEffect` = auc.rbe_splsda, 
                       ComBat = auc.combat_splsda, 
                       `wPLSDA-batch` = auc.wplsda_batch_splsda, 
                       `swPLSDA-batch` = auc.swplsda_batch_splsda)
  
  #print(i)
  
}

4.2.4 Figures

# global variance (RDA)
prop.gvar.all <- rbind(`Before correction` = colMeans(gvar.before),
                       `Ground-truth data` = colMeans(gvar.clean),
                       removeBatchEffect = colMeans(gvar.rbe),
                       ComBat = colMeans(gvar.combat),
                       `wPLSDA-batch` = colMeans(gvar.wplsdab),
                       `swPLSDA-batch` = colMeans(gvar.swplsdab),
                       `PLSDA-batch` = colMeans(gvar.plsdab),
                       `sPLSDA-batch` = colMeans(gvar.splsdab))

prop.gvar.all[prop.gvar.all < 0] = 0
prop.gvar.all <- t(apply(prop.gvar.all, 1, function(x){x/sum(x)}))
colnames(prop.gvar.all) <- c('Treatment', 'Intersection', 'Batch', 'Residuals')

partVar_plot(prop.df = prop.gvar.all)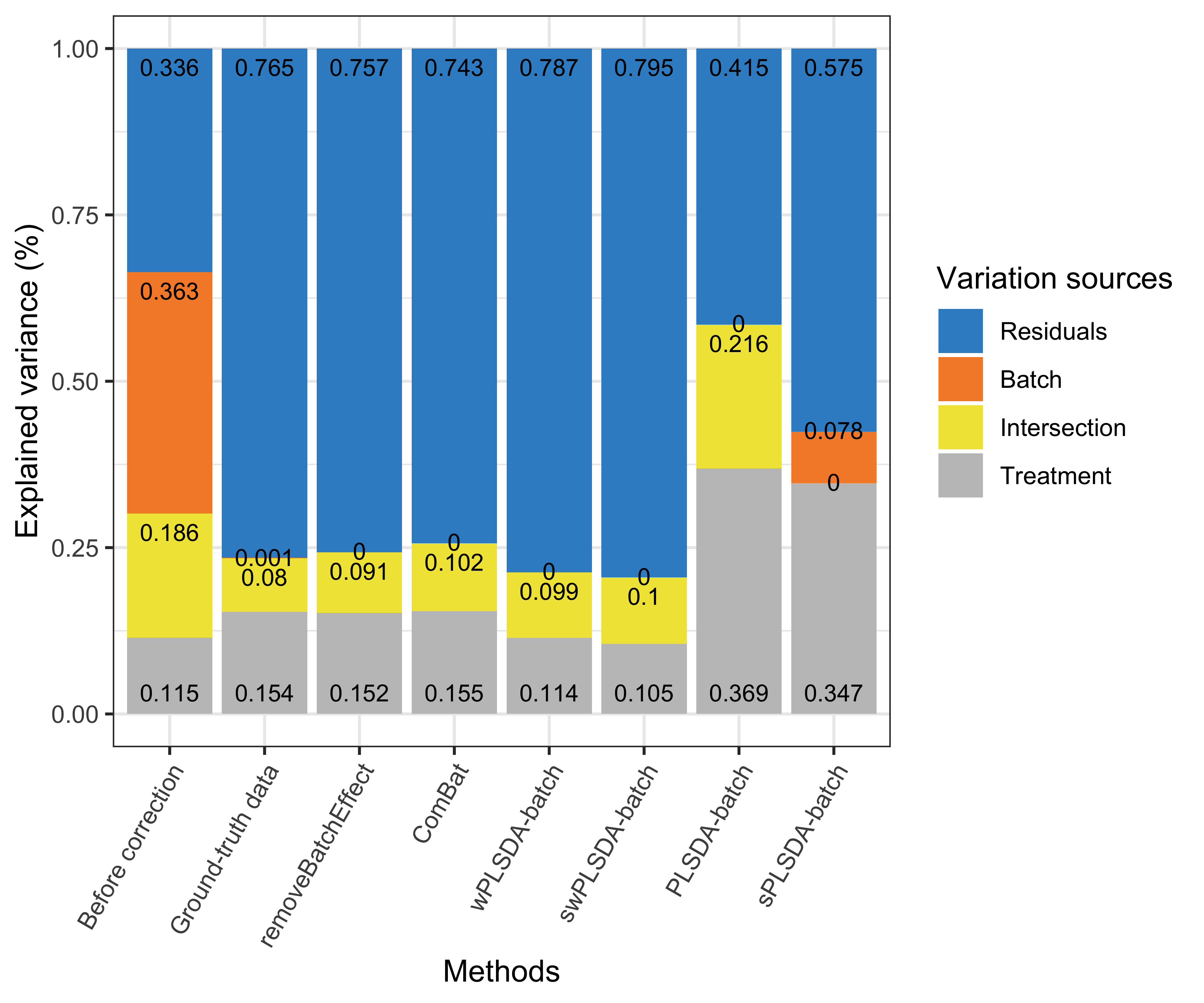
Figure 4: Simulation studies (two batch groups): comparison of explained variance before and after batch effect correction for the unbalanced batch × treatment design.

Figure 4.4: Figure 4: Simulation studies (two batch groups): comparison of explained variance before and after batch effect correction for the unbalanced batch × treatment design.

For a strong unbalanced batch \(\times\) treatment design, we observed the presence of intersectional variance explained by both batch and treatment effects, as expected. This source of variance is also present in the ground-truth data but should be smaller compared to the uncorrected data. Both unweighted PLSDA-batch and sPLSDA-batch performed poorly for such design - for PLSDA-batch the intersectional variance increased while for sPLSDA-batch the batch variance was not entirely removed. The other methods were successful in removing batch variance. removeBatchEffect and ComBat explained a proportion of variance by treatment similar to the ground-truth data, while wPLSDA-batch and swPLSDA-batch explained slightly less treatment variance.

###############################################################################
# individual variance (R2)
## boxplot
# class
gclass <- c(rep('Treatment only', p_trt_relevant), 
            rep('Batch only', (p_total - p_trt_relevant)))
gclass[intersect(true.trt, true.batch)] = 'Treatment & batch'
gclass[setdiff(1:p_total, union(true.trt, true.batch))] = 'No effect'

gclass <- factor(gclass, levels = c('Treatment & batch', 
                                    'Treatment only', 
                                    'Batch only', 
                                    'No effect'))

before.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.before), 
                                      rowMeans(r2.batch.before)), 
                               type = as.factor(rep(c('Treatment','Batch'), 
                                                    each = 300)),
                               class = rep(gclass,2))
clean.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.clean), 
                                     rowMeans(r2.batch.clean)), 
                              type = as.factor(rep(c('Treatment','Batch'), 
                                                   each = 300)),
                              class = rep(gclass,2))
rbe.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.rbe), 
                                   rowMeans(r2.batch.rbe)), 
                            type = as.factor(rep(c('Treatment','Batch'), 
                                                 each = 300)),
                            class = rep(gclass,2))
combat.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.combat), 
                                      rowMeans(r2.batch.combat)), 
                               type = as.factor(rep(c('Treatment','Batch'), 
                                                    each = 300)),
                               class = rep(gclass,2))
wplsda_batch.r2.df.ggp <- 
  data.frame(r2 = c(rowMeans(r2.trt.wplsdab), 
                    rowMeans(r2.batch.wplsdab)), 
             type = as.factor(rep(c('Treatment','Batch'), 
                                  each = 300)),
             class = rep(gclass,2))
swplsda_batch.r2.df.ggp <- 
  data.frame(r2 = c(rowMeans(r2.trt.swplsdab), 
                    rowMeans(r2.batch.swplsdab)), 
             type = as.factor(rep(c('Treatment','Batch'),
                                  each = 300)),
             class = rep(gclass,2))

all.r2.df.ggp <- rbind(before.r2.df.ggp, clean.r2.df.ggp,
                       rbe.r2.df.ggp, combat.r2.df.ggp,
                       wplsda_batch.r2.df.ggp, swplsda_batch.r2.df.ggp)

all.r2.df.ggp$methods <- rep(c('Before correction', 
                               'Ground-truth data', 
                               'removeBatchEffect', 
                               'ComBat',
                               'wPLSDA-batch', 
                               'swPLSDA-batch'), each = 600)

all.r2.df.ggp$methods <- factor(all.r2.df.ggp$methods, 
                                levels = unique(all.r2.df.ggp$methods))

ggplot(all.r2.df.ggp, aes(x = type, y = r2, fill = class)) +
  geom_boxplot(alpha = 0.80) +
  theme_bw() + 
  theme(text = element_text(size = 18),
        axis.title.x = element_blank(),
        axis.title.y = element_blank(),
        panel.grid.minor.x = element_blank(),
        panel.grid.major.x = element_blank(),
        legend.position = "right") + facet_grid(class ~ methods) + 
  scale_fill_manual(values=c('dark gray', color.mixo(4), 
                             color.mixo(5), color.mixo(9)))
Figure 5: Simulation studies (two batch groups): R2 values for each microbial variable before and after batch effect correction for the unbalanced batch × treatment design.

Figure 4.5: Figure 5: Simulation studies (two batch groups): R2 values for each microbial variable before and after batch effect correction for the unbalanced batch × treatment design. 

################################################################################
## barplot
# class
before.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.before), gclass, sum), 
                    tapply(rowMeans(r2.batch.before), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

clean.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.clean), gclass, sum), 
                    tapply(rowMeans(r2.batch.clean), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

rbe.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.rbe), gclass, sum), 
                    tapply(rowMeans(r2.batch.rbe), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

combat.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.combat), gclass, sum), 
                    tapply(rowMeans(r2.batch.combat), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

wplsda_batch.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.wplsdab), gclass, sum), 
                    tapply(rowMeans(r2.batch.wplsdab), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

swplsda_batch.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.swplsdab), gclass, sum), 
                    tapply(rowMeans(r2.batch.swplsdab), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))


all.r2.df.bp <- rbind(before.r2.df.bp, clean.r2.df.bp,
                      rbe.r2.df.bp, combat.r2.df.bp,
                      wplsda_batch.r2.df.bp, swplsda_batch.r2.df.bp)


all.r2.df.bp$methods <- rep(c('Before correction', 
                              'Ground-truth data', 
                              'removeBatchEffect', 
                              'ComBat',
                              'wPLSDA-batch', 
                              'swPLSDA-batch'), each = 8)

all.r2.df.bp$methods <- factor(all.r2.df.bp$methods, 
                               levels = unique(all.r2.df.bp$methods))

ggplot(all.r2.df.bp, aes(x = type, y = r2, fill = class)) +
  geom_bar(stat="identity") + 
  theme_bw() + 
  theme(text = element_text(size = 18),
        axis.title.x = element_blank(),
        axis.title.y = element_blank(),
        panel.grid.minor.x = element_blank(),
        panel.grid.major.x = element_blank(),
        legend.position = "right") + facet_grid(class ~ methods) + 
  scale_fill_manual(values=c('dark gray', color.mixo(4), 
                             color.mixo(5), color.mixo(9)))
Figure 6: Simulation studies (two batch groups): the sum of R2 values for each microbial variable before and after batch effect correction for the unbalanced batch × treatment design.

Figure 4.6: Figure 6: Simulation studies (two batch groups): the sum of R2 values for each microbial variable before and after batch effect correction for the unbalanced batch × treatment design.

We observed similar performance for removeBatchEffect and ComBat for the unbalanced design compared to the balanced design. With wPLSDA-batch and swPLSDA-batch, variables with both treatment and batch effects explained less treatment variance after correction, compared to the ground-truth data. However, for the other variables, wPLSDA-batch and its sparse version performed as similar as the ground-truth data.

# precision & recall & F1 (ANOVA & sPLSDA)
## mean
acc_mean <- rbind(colMeans(precision_limma), colMeans(recall_limma), 
                  colMeans(F1_limma), c(colMeans(auc_splsda), sva = NA))
rownames(acc_mean) <- c('Precision', 'Recall', 'F1', 'AUC')
colnames(acc_mean) <- c('Before correction', 'Ground-truth data', 
                        'removeBatchEffect', 'ComBat', 
                        'wPLSDA-batch', 'swPLSDA-batch', 'SVA')
acc_mean <- format(acc_mean, digits = 3)
knitr::kable(acc_mean, caption = 'Table 6 Simulation studies (two batch groups): summary of accuracy measurements before and after batch effect correction for the unbalanced batch × treatment design (mean).')
Table 4.3: Table 6 Simulation studies (two batch groups): summary of accuracy measurements before and after batch effect correction for the unbalanced batch × treatment design (mean).
Before correction Ground-truth data removeBatchEffect ComBat wPLSDA-batch swPLSDA-batch SVA
Precision 0.385 0.973 0.901 0.834 0.943 0.943 0.401
Recall 0.825 0.895 0.910 0.919 0.888 0.862 0.918
F1 0.525 0.932 0.903 0.873 0.914 0.900 0.558
AUC 0.704 0.967 0.963 0.962 0.965 0.954 NA

In the unbalanced design, the precision of SVA is low and very similar to the original data, indicating that the performance of SVA heavily depends on the experimental design and is likely to overfit. This may explain the somewhat inflated results of SVA in the balanced design case. wPLSDA-batch performed best with results close to those from the ground-truth data.

## sd
acc_sd <- rbind(apply(precision_limma, 2, sd), apply(recall_limma, 2, sd), 
                apply(F1_limma, 2, sd), c(apply(auc_splsda, 2, sd), NA))
rownames(acc_sd) <- c('Precision', 'Recall', 'F1', 'AUC')
colnames(acc_sd) <- c('Before correction', 'Ground-truth data', 
                      'removeBatchEffect', 'ComBat', 
                      'wPLSDA-batch', 'swPLSDA-batch', 'SVA')
acc_sd <- format(acc_sd, digits = 1)
knitr::kable(acc_sd, caption = 'Table 7 Simulation studies (two batch groups): summary of accuracy measurements before and after batch effect correction for the unbalanced batch × treatment design (standard deviation).')
Table 4.4: Table 7 Simulation studies (two batch groups): summary of accuracy measurements before and after batch effect correction for the unbalanced batch × treatment design (standard deviation).
Before correction Ground-truth data removeBatchEffect ComBat wPLSDA-batch swPLSDA-batch SVA
Precision 0.01 0.05 0.09 0.08 0.05 0.05 0.02
Recall 0.03 0.03 0.03 0.03 0.03 0.03 0.03
F1 0.01 0.03 0.05 0.05 0.03 0.03 0.02
AUC 0.06 0.02 0.02 0.01 0.01 0.02 NA

4.3 Simulations (three batch groups)

4.3.1 Balanced batch \(\times\) treatment design

The balanced batch \(\times\) treatment experimental design included 6 samples from three batches respectively in each treatment group.

Table 8: Balanced batch \(\times\) treatment design in the simulation study

Trt1 Trt2
Batch1 6 6
Batch2 6 6
Batch3 6 6 
nitr <- 50
N = 36
p_total = 300
p_trt_relevant = 100 
p_bat_relevant = 200 

# global variance (RDA)
gvar.before <- gvar.clean <- 
  gvar.rbe <- gvar.combat <- 
  gvar.plsdab <- gvar.splsdab <- data.frame(treatment = NA, batch = NA,  
                                            intersection = NA, 
                                            residual = NA)

# individual variance (R2)
r2.trt.before <- r2.trt.clean <- 
  r2.trt.rbe  <- r2.trt.combat <- 
  r2.trt.plsdab <- r2.trt.splsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                       ncol = nitr))
r2.batch.before <- r2.batch.clean <- 
  r2.batch.rbe  <- r2.batch.combat <- 
  r2.batch.plsdab <- r2.batch.splsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                           ncol = nitr))

# precision & recall & F1 (ANOVA)
precision_limma <- recall_limma <- F1_limma <- 
  data.frame(before = NA, clean = NA, 
             rbe = NA, combat = NA, 
             plsda_batch = NA, splsda_batch = NA, 
             sva = NA)

# auc (splsda)
auc_splsda <- 
  data.frame(before = NA, clean = NA, 
             rbe = NA, combat = NA, 
             plsda_batch = NA, splsda_batch = NA)


set.seed(70)
data.cor.res = corStruct(p = 300, zero_prob = 0.7)

for(i in 1: nitr){
  ### initial setup ###
  simulation <- simData_mnegbinom(batch.group = 3,
                                  mean.batch = 7, 
                                  sd.batch = 8, 
                                  mean.trt = 3, 
                                  sd.trt = 2, 
                                  mean.bg = 0, 
                                  sd.bg = 0.2, 
                                  N = 36, 
                                  p_total = 300, 
                                  p_trt_relevant = 100, 
                                  p_bat_relevant = 200, 
                                  percentage_overlap_samples = 0.5, 
                                  percentage_overlap_variables = 0.5, 
                                  data.cor = data.cor.res$data.cor, 
                                  disp = 10, prob_zero = 0, 
                                  seeds = i)
  
  set.seed(i)
  raw_count <- simulation$data
  raw_count_clean <- simulation$cleanData
  
  ## log transformation
  data_log <- log(raw_count + 1)
  data_log_clean <- log(raw_count_clean + 1)
  
  trt <- simulation$Y.trt
  batch <- simulation$Y.bat
  
  true.trt <- simulation$true.trt
  true.batch <- simulation$true.batch
  
  Batch_Trt.factors <- data.frame(Batch = batch, Treatment = trt)
  
  ### Original ###
  X <- data_log
  
  ### Clean data ###
  X.clean <- data_log_clean
  
  #####
  rownames(X) = rownames(X.clean) = names(trt) = names(batch) = 
    paste0('sample', 1:N)
  
  colnames(X) = colnames(X.clean) = paste0('otu', 1:p_total)
  
  ### Before correction ###
  # global variance (RDA)
  rda.before = varpart(scale(X), ~ Treatment, ~ Batch, 
                       data = Batch_Trt.factors)
  gvar.before[i,] <- rda.before$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.before <- lmFit(t(scale(X)), design = model.matrix(~ as.factor(trt)))
  fit.result.before <- topTable(eBayes(fit.before), coef = 2, number = p_total)
  otu.sig.before <- 
    rownames(fit.result.before)[fit.result.before$adj.P.Val <= 0.05]
  
  precision_limma.before <- 
    length(intersect(colnames(X)[true.trt], otu.sig.before))/
    length(otu.sig.before)
  recall_limma.before <- 
    length(intersect(colnames(X)[true.trt], otu.sig.before))/length(true.trt)
  F1_limma.before <- 
    (2*precision_limma.before*recall_limma.before)/
    (precision_limma.before + recall_limma.before)
  
  ## replace NA value with 0
  if(precision_limma.before == 'NaN'){
    precision_limma.before = 0
  }
  if(F1_limma.before == 'NaN'){
    F1_limma.before = 0
  }
  
  # individual variance (R2)
  indiv.trt.before <- c()
  indiv.batch.before <- c()
  for(c in seq_len(ncol(X))){
    fit.res1 <- lm(scale(X)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.before <- c(indiv.trt.before, fit.summary1$r.squared)
    indiv.batch.before <- c(indiv.batch.before, fit.summary2$r.squared)
  }
  r2.trt.before[ ,i] <-  indiv.trt.before
  r2.batch.before[ ,i] <-  indiv.batch.before
  
  
  # auc (sPLSDA)
  fit.before_plsda <- splsda(X = X, Y = trt, ncomp = 1)
  
  true.response <- rep(0, p_total)
  true.response[true.trt] = 1
  before.predictor <- as.numeric(abs(fit.before_plsda$loadings$X))
  roc.before_splsda <- roc(true.response, before.predictor, auc = TRUE)
  auc.before_splsda <- roc.before_splsda$auc
  
  
  ##############################################################################
  ### Ground-truth data ###
  # global variance (RDA)
  rda.clean = varpart(scale(X.clean), ~ Treatment, ~ Batch, 
                      data = Batch_Trt.factors)
  gvar.clean[i, ] <- rda.clean$part$indfract$Adj.R.squared
  
  
  # precision & recall & F1 (ANOVA)
  fit.clean <- lmFit(t(scale(X.clean)), design = model.matrix(~ as.factor(trt)))
  fit.result.clean <- topTable(eBayes(fit.clean), coef = 2, number = p_total)
  otu.sig.clean <- 
    rownames(fit.result.clean)[fit.result.clean$adj.P.Val <= 0.05]
  
  precision_limma.clean <- 
    length(intersect(colnames(X)[true.trt], otu.sig.clean))/
    length(otu.sig.clean)
  recall_limma.clean<- 
    length(intersect(colnames(X)[true.trt], otu.sig.clean))/length(true.trt)
  F1_limma.clean <- 
    (2*precision_limma.clean*recall_limma.clean)/
    (precision_limma.clean + recall_limma.clean)
  
  ## replace NA value with 0
  if(precision_limma.clean == 'NaN'){
    precision_limma.clean = 0
  }
  if(F1_limma.clean == 'NaN'){
    F1_limma.clean = 0
  }
  
  # individual variance (R2)
  indiv.trt.clean <- c()
  indiv.batch.clean <- c()
  for(c in seq_len(ncol(X.clean))){
    fit.res1 <- lm(scale(X.clean)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.clean)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.clean <- c(indiv.trt.clean, fit.summary1$r.squared)
    indiv.batch.clean <- c(indiv.batch.clean, fit.summary2$r.squared)
  }
  r2.trt.clean[ ,i] <-  indiv.trt.clean
  r2.batch.clean[ ,i] <-  indiv.batch.clean
  
  # auc (sPLSDA)
  fit.clean_plsda <- splsda(X = X.clean, Y = trt, ncomp = 1)
  
  clean.predictor <- as.numeric(abs(fit.clean_plsda$loadings$X))
  roc.clean_splsda <- roc(true.response, clean.predictor, auc = TRUE)
  auc.clean_splsda <- roc.clean_splsda$auc
  
  ##############################################################################
  ### removeBatchEffect corrected data ###
  X.rbe <-t(removeBatchEffect(t(X), batch = batch, 
                              design = model.matrix(~ as.factor(trt))))
  
  # global variance (RDA)
  rda.rbe = varpart(scale(X.rbe), ~ Treatment, ~ Batch, 
                    data = Batch_Trt.factors)
  gvar.rbe[i, ] <- rda.rbe$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.rbe <- lmFit(t(scale(X.rbe)), 
                   design = model.matrix( ~ as.factor(trt)))
  fit.result.rbe <- topTable(eBayes(fit.rbe), coef = 2, number = p_total)
  otu.sig.rbe <- rownames(fit.result.rbe)[fit.result.rbe$adj.P.Val <= 0.05]
  
  precision_limma.rbe <- length(intersect(colnames(X)[true.trt], otu.sig.rbe))/
    length(otu.sig.rbe)
  recall_limma.rbe <- length(intersect(colnames(X)[true.trt], otu.sig.rbe))/
    length(true.trt)
  F1_limma.rbe <- (2*precision_limma.rbe*recall_limma.rbe)/
    (precision_limma.rbe + recall_limma.rbe)
  
  ## replace NA value with 0
  if(precision_limma.rbe == 'NaN'){
    precision_limma.rbe = 0
  }
  if(F1_limma.rbe == 'NaN'){
    F1_limma.rbe = 0
  }
  
  # individual variance (R2)
  indiv.trt.rbe <- c()
  indiv.batch.rbe <- c()
  for(c in seq_len(ncol(X.rbe))){
    fit.res1 <- lm(scale(X.rbe)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.rbe)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.rbe <- c(indiv.trt.rbe, fit.summary1$r.squared)
    indiv.batch.rbe <- c(indiv.batch.rbe, fit.summary2$r.squared)
  }
  r2.trt.rbe[ ,i] <-  indiv.trt.rbe
  r2.batch.rbe[ ,i] <-  indiv.batch.rbe
  
  
  # auc (sPLSDA)
  fit.rbe_plsda <- splsda(X = X.rbe, Y = trt, ncomp = 1)
  
  rbe.predictor <- as.numeric(abs(fit.rbe_plsda$loadings$X))
  roc.rbe_splsda <- roc(true.response, rbe.predictor, auc = TRUE)
  auc.rbe_splsda <- roc.rbe_splsda$auc
  
  ##############################################################################
  ### ComBat corrected data ###
  X.combat <- t(ComBat(dat = t(X), batch = batch, 
                       mod = model.matrix( ~ as.factor(trt))))
  
  # global variance (RDA)
  rda.combat = varpart(scale(X.combat), ~ Treatment, ~ Batch, 
                       data = Batch_Trt.factors)
  gvar.combat[i, ] <- rda.combat$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.combat <- lmFit(t(scale(X.combat)), 
                      design = model.matrix( ~ as.factor(trt)))
  fit.result.combat <- topTable(eBayes(fit.combat), coef = 2, number = p_total)
  otu.sig.combat <- rownames(fit.result.combat)[fit.result.combat$adj.P.Val <= 
                                                  0.05]
  
  precision_limma.combat <- 
    length(intersect(colnames(X)[true.trt], otu.sig.combat))/
    length(otu.sig.combat)
  recall_limma.combat <- 
    length(intersect(colnames(X)[true.trt], otu.sig.combat))/
    length(true.trt)
  F1_limma.combat <- (2*precision_limma.combat*recall_limma.combat)/
    (precision_limma.combat + recall_limma.combat)
  
  ## replace NA value with 0
  if(precision_limma.combat == 'NaN'){
    precision_limma.combat = 0
  }
  if(F1_limma.combat == 'NaN'){
    F1_limma.combat = 0
  }
  
  # individual variance (R2)
  indiv.trt.combat <- c()
  indiv.batch.combat <- c()
  for(c in seq_len(ncol(X.combat))){
    fit.res1 <- lm(scale(X.combat)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.combat)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.combat <- c(indiv.trt.combat, fit.summary1$r.squared)
    indiv.batch.combat <- c(indiv.batch.combat, fit.summary2$r.squared)
  }
  r2.trt.combat[ ,i] <-  indiv.trt.combat
  r2.batch.combat[ ,i] <-  indiv.batch.combat
  
  
  # auc (sPLSDA)
  fit.combat_plsda <- splsda(X = X.combat, Y = trt, ncomp = 1)
  
  combat.predictor <- as.numeric(abs(fit.combat_plsda$loadings$X))
  roc.combat_splsda <- roc(true.response, combat.predictor, auc = TRUE)
  auc.combat_splsda <- roc.combat_splsda$auc
  
  
  ##############################################################################
  ### PLSDA-batch corrected data ###
  X.plsda_batch.correct <- PLSDA_batch(X = X, 
                                       Y.trt = trt, Y.bat = batch, 
                                       ncomp.trt = 1, ncomp.bat = 2)
  X.plsda_batch <- X.plsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.plsda_batch = varpart(scale(X.plsda_batch), ~ Treatment, ~ Batch, 
                            data = Batch_Trt.factors)
  gvar.plsdab[i, ] <- rda.plsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.plsda_batch <- lmFit(t(scale(X.plsda_batch)), 
                           design = model.matrix( ~ as.factor(trt)))
  fit.result.plsda_batch <- topTable(eBayes(fit.plsda_batch), 
                                     coef = 2, number = p_total)
  otu.sig.plsda_batch <- rownames(fit.result.plsda_batch)[
    fit.result.plsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.plsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.plsda_batch))/
    length(otu.sig.plsda_batch)
  recall_limma.plsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.plsda_batch))/
    length(true.trt)
  F1_limma.plsda_batch <- 
    (2*precision_limma.plsda_batch*recall_limma.plsda_batch)/
    (precision_limma.plsda_batch + recall_limma.plsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.plsda_batch == 'NaN'){
    precision_limma.plsda_batch = 0
  }
  if(F1_limma.plsda_batch == 'NaN'){
    F1_limma.plsda_batch = 0
  }
  
  # individual variance (R2)
  indiv.trt.plsda_batch <- c()
  indiv.batch.plsda_batch <- c()
  for(c in seq_len(ncol(X.plsda_batch))){
    fit.res1 <- lm(scale(X.plsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.plsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.plsda_batch <- c(indiv.trt.plsda_batch, 
                               fit.summary1$r.squared)
    indiv.batch.plsda_batch <- c(indiv.batch.plsda_batch, 
                                 fit.summary2$r.squared)
  }
  r2.trt.plsdab[ ,i] <-  indiv.trt.plsda_batch
  r2.batch.plsdab[ ,i] <-  indiv.batch.plsda_batch
  
  # auc (sPLSDA)
  fit.plsda_batch_plsda <- splsda(X = X.plsda_batch, Y = trt, ncomp = 1)
  
  plsda_batch.predictor <- as.numeric(abs(fit.plsda_batch_plsda$loadings$X))
  roc.plsda_batch_splsda <- roc(true.response, 
                                plsda_batch.predictor, auc = TRUE)
  auc.plsda_batch_splsda <- roc.plsda_batch_splsda$auc
  
  ##############################################################################
  ### sPLSDA-batch corrected data ###
  X.splsda_batch.correct <- PLSDA_batch(X = X, 
                                        Y.trt = trt, 
                                        Y.bat = batch, 
                                        ncomp.trt = 1, 
                                        keepX.trt = length(true.trt), 
                                        ncomp.bat = 2)
  X.splsda_batch <- X.splsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.splsda_batch = varpart(scale(X.splsda_batch), ~ Treatment, ~ Batch, 
                             data = Batch_Trt.factors)
  gvar.splsdab[i, ] <- rda.splsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.splsda_batch <- lmFit(t(scale(X.splsda_batch)), 
                            design = model.matrix( ~ as.factor(trt)))
  fit.result.splsda_batch <- topTable(eBayes(fit.splsda_batch), coef = 2, 
                                      number = p_total)
  otu.sig.splsda_batch <- rownames(fit.result.splsda_batch)[
    fit.result.splsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.splsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.splsda_batch))/
    length(otu.sig.splsda_batch)
  recall_limma.splsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.splsda_batch))/
    length(true.trt)
  F1_limma.splsda_batch <- 
    (2*precision_limma.splsda_batch*recall_limma.splsda_batch)/
    (precision_limma.splsda_batch + recall_limma.splsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.splsda_batch == 'NaN'){
    precision_limma.splsda_batch = 0
  }
  if(F1_limma.splsda_batch == 'NaN'){
    F1_limma.splsda_batch = 0
  }
  
  
  # individual variance (R2)
  indiv.trt.splsda_batch <- c()
  indiv.batch.splsda_batch <- c()
  for(c in seq_len(ncol(X.splsda_batch))){
    fit.res1 <- lm(scale(X.splsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.splsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.splsda_batch <- c(indiv.trt.splsda_batch, 
                                fit.summary1$r.squared)
    indiv.batch.splsda_batch <- c(indiv.batch.splsda_batch, 
                                  fit.summary2$r.squared)
  }
  r2.trt.splsdab[ ,i] <-  indiv.trt.splsda_batch
  r2.batch.splsdab[ ,i] <-  indiv.batch.splsda_batch
  
  # auc (sPLSDA)
  fit.splsda_batch_plsda <- splsda(X = X.splsda_batch, Y = trt, ncomp = 1)
  
  splsda_batch.predictor <- as.numeric(abs(fit.splsda_batch_plsda$loadings$X))
  roc.splsda_batch_splsda <- roc(true.response, 
                                 splsda_batch.predictor, auc = TRUE)
  auc.splsda_batch_splsda <- roc.splsda_batch_splsda$auc
  
  ##############################################################################
  ### SVA ###
  X.mod <- model.matrix(~ as.factor(trt))
  X.mod0 <- model.matrix(~ 1, data = as.factor(trt))
  X.sva.n <- num.sv(dat = t(X), mod = X.mod, method = 'leek')
  X.sva <- sva(t(X), X.mod, X.mod0, n.sv = X.sva.n)
  
  X.mod.batch <- cbind(X.mod, X.sva$sv)
  X.mod0.batch <- cbind(X.mod0, X.sva$sv)
  X.sva.p <- f.pvalue(t(X), X.mod.batch, X.mod0.batch)
  X.sva.p.adj <- p.adjust(X.sva.p, method = 'fdr')
  
  otu.sig.sva <- which(X.sva.p.adj <= 0.05)
  
  # precision & recall & F1 (ANOVA)
  precision_limma.sva <- 
    length(intersect(true.trt, otu.sig.sva))/length(otu.sig.sva)
  recall_limma.sva <- 
    length(intersect(true.trt, otu.sig.sva))/length(true.trt)
  F1_limma.sva <- (2*precision_limma.sva*recall_limma.sva)/
    (precision_limma.sva + recall_limma.sva)
  
  ## replace NA value with 0
  if(precision_limma.sva == 'NaN'){
    precision_limma.sva = 0
  }
  if(F1_limma.sva == 'NaN'){
    F1_limma.sva = 0
  }
  
  
  # summary
  # precision & recall & F1 (ANOVA)
  precision_limma[i, ] <- c(`Before correction` = precision_limma.before, 
                            `Ground-truth data` = precision_limma.clean,
                            `removeBatchEffect` = precision_limma.rbe,
                            ComBat = precision_limma.combat,
                            `PLSDA-batch` = precision_limma.plsda_batch,
                            `sPLSDA-batch` = precision_limma.splsda_batch,
                            SVA = precision_limma.sva)
  
  recall_limma[i, ] <- c(`Before correction` = recall_limma.before, 
                         `Ground-truth data` = recall_limma.clean,
                         `removeBatchEffect` = recall_limma.rbe,
                         ComBat = recall_limma.combat,
                         `PLSDA-batch` = recall_limma.plsda_batch,
                         `sPLSDA-batch` = recall_limma.splsda_batch,
                         SVA = recall_limma.sva)
  
  F1_limma[i, ] <- c(`Before correction` = F1_limma.before, 
                     `Ground-truth data` = F1_limma.clean,
                     `removeBatchEffect` = F1_limma.rbe,
                     ComBat = F1_limma.combat,
                     `PLSDA-batch` = F1_limma.plsda_batch,
                     `sPLSDA-batch` = F1_limma.splsda_batch,
                     SVA = F1_limma.sva)
  
  # auc (splsda)
  auc_splsda[i, ] <- c(`Before correction` = auc.before_splsda, 
                       `Ground-truth data` = auc.clean_splsda, 
                       `removeBatchEffect` = auc.rbe_splsda, 
                       ComBat = auc.combat_splsda, 
                       `PLSDA-batch` = auc.plsda_batch_splsda, 
                       `sPLSDA-batch` = auc.splsda_batch_splsda)
  
  # print(i)
  
}

4.3.2 Figures

# global variance (RDA)
prop.gvar.all <- rbind(`Before correction` = colMeans(gvar.before),
                       `Ground-truth data` = colMeans(gvar.clean),
                       removeBatchEffect = colMeans(gvar.rbe),
                       ComBat = colMeans(gvar.combat),
                       `PLSDA-batch` = colMeans(gvar.plsdab),
                       `sPLSDA-batch` = colMeans(gvar.splsdab))

prop.gvar.all[prop.gvar.all < 0] = 0
prop.gvar.all <- t(apply(prop.gvar.all, 1, function(x){x/sum(x)}))
colnames(prop.gvar.all) <- c('Treatment', 'Intersection', 'Batch', 'Residuals')

partVar_plot(prop.df = prop.gvar.all)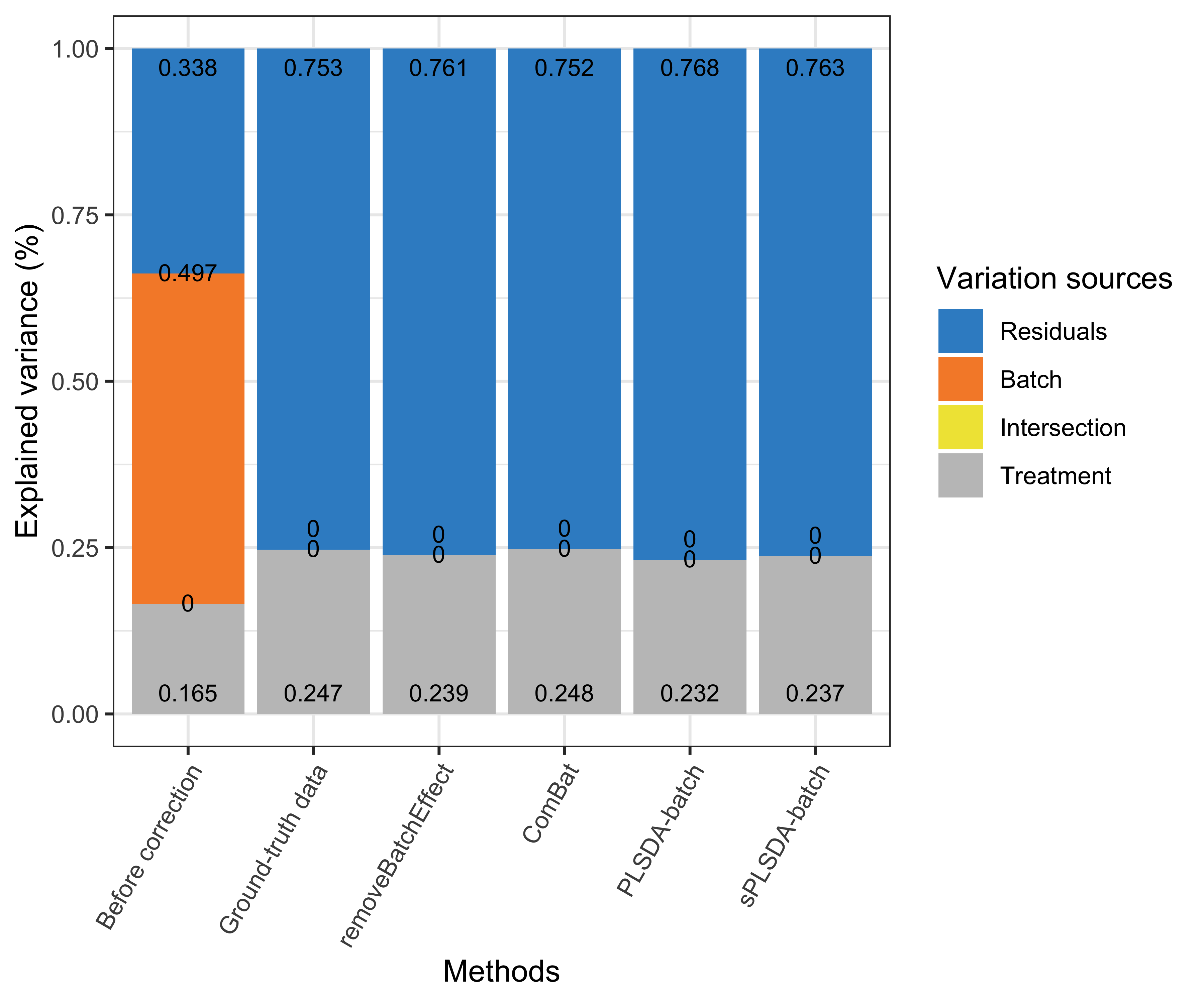
Figure 7: Simulation studies (three batch groups): comparison of explained variance before and after batch effect correction for the balanced batch × treatment design.

Figure 4.7: Figure 7: Simulation studies (three batch groups): comparison of explained variance before and after batch effect correction for the balanced batch × treatment design. 

################################################################################
# individual variance (R2)
## boxplot
# class
gclass <- c(rep('Treatment only', p_trt_relevant), 
            rep('Batch only', (p_total - p_trt_relevant)))
gclass[intersect(true.trt, true.batch)] = 'Treatment & batch'
gclass[setdiff(1:p_total, union(true.trt, true.batch))] = 'No effect'

gclass <- factor(gclass, levels = c('Treatment & batch', 
                                    'Treatment only', 
                                    'Batch only', 
                                    'No effect'))

before.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.before), 
                                      rowMeans(r2.batch.before)), 
                               type = as.factor(rep(c('Treatment','Batch'), 
                                                    each = 300)),
                               class = rep(gclass,2))
clean.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.clean), 
                                     rowMeans(r2.batch.clean)), 
                              type = as.factor(rep(c('Treatment','Batch'), 
                                                   each = 300)),
                              class = rep(gclass,2))
rbe.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.rbe), 
                                   rowMeans(r2.batch.rbe)), 
                            type = as.factor(rep(c('Treatment','Batch'), 
                                                 each = 300)),
                            class = rep(gclass,2))
combat.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.combat), 
                                      rowMeans(r2.batch.combat)), 
                               type = as.factor(rep(c('Treatment','Batch'), 
                                                    each = 300)),
                               class = rep(gclass,2))
plsda_batch.r2.df.ggp <- 
  data.frame(r2 = c(rowMeans(r2.trt.plsdab), 
                    rowMeans(r2.batch.plsdab)), 
             type = as.factor(rep(c('Treatment','Batch'), 
                                  each = 300)),
             class = rep(gclass,2))
splsda_batch.r2.df.ggp <- 
  data.frame(r2 = c(rowMeans(r2.trt.splsdab), 
                    rowMeans(r2.batch.splsdab)), 
             type = as.factor(rep(c('Treatment','Batch'), 
                                  each = 300)),
             class = rep(gclass,2))

all.r2.df.ggp <- rbind(before.r2.df.ggp, clean.r2.df.ggp,
                       rbe.r2.df.ggp, combat.r2.df.ggp,
                       plsda_batch.r2.df.ggp, splsda_batch.r2.df.ggp)

all.r2.df.ggp$methods <- rep(c('Before correction', 
                               'Ground-truth data', 
                               'removeBatchEffect', 
                               'ComBat',
                               'PLSDA-batch', 
                               'sPLSDA-batch'), each = 600)

all.r2.df.ggp$methods <- factor(all.r2.df.ggp$methods, 
                                levels = unique(all.r2.df.ggp$methods))

ggplot(all.r2.df.ggp, aes(x = type, y = r2, fill = class)) +
  geom_boxplot(alpha = 0.80) +
  theme_bw() + 
  theme(text = element_text(size = 18),
        axis.title.x = element_blank(),
        axis.title.y = element_blank(),
        panel.grid.minor.x = element_blank(),
        panel.grid.major.x = element_blank(),
        legend.position = "right") + facet_grid(class ~ methods) + 
  scale_fill_manual(values=c('dark gray', color.mixo(4), 
                             color.mixo(5), color.mixo(9)))
Figure 8: Simulation studies (three batch groups): R2 values for each microbial variable before and after batch effect correction for the balanced batch × treatment design.

Figure 4.8: Figure 8: Simulation studies (three batch groups): R2 values for each microbial variable before and after batch effect correction for the balanced batch × treatment design. 

################################################################################
## barplot
# class
before.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.before), gclass, sum),
                    tapply(rowMeans(r2.batch.before), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

clean.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.clean), gclass, sum),
                    tapply(rowMeans(r2.batch.clean), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

rbe.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.rbe), gclass, sum), 
                    tapply(rowMeans(r2.batch.rbe), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

combat.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.combat), gclass, sum),
                    tapply(rowMeans(r2.batch.combat), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

plsda_batch.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.plsdab), gclass, sum), 
                    tapply(rowMeans(r2.batch.plsdab), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

splsda_batch.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.splsdab), gclass, sum), 
                    tapply(rowMeans(r2.batch.splsdab), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))


all.r2.df.bp <- rbind(before.r2.df.bp, clean.r2.df.bp,
                      rbe.r2.df.bp, combat.r2.df.bp,
                      plsda_batch.r2.df.bp, splsda_batch.r2.df.bp)


all.r2.df.bp$methods <- rep(c('Before correction', 
                              'Ground-truth data', 
                              'removeBatchEffect', 
                              'ComBat',
                              'PLSDA-batch', 
                              'sPLSDA-batch'), each = 8)

all.r2.df.bp$methods <- factor(all.r2.df.bp$methods, 
                               levels = unique(all.r2.df.bp$methods))

ggplot(all.r2.df.bp, aes(x = type, y = r2, fill = class)) +
  geom_bar(stat="identity") + 
  theme_bw() + 
  theme(text = element_text(size = 18),
        axis.title.x = element_blank(),
        axis.title.y = element_blank(),
        panel.grid.minor.x = element_blank(),
        panel.grid.major.x = element_blank(),
        legend.position = "right") + facet_grid(class ~ methods) +
  scale_fill_manual(values=c('dark gray', color.mixo(4), 
                             color.mixo(5), color.mixo(9)))
Figure 9: Simulation studies (three batch groups): the sum of R2 values for each microbial variable before and after batch effect correction for the balanced batch × treatment design.

Figure 4.9: Figure 9: Simulation studies (three batch groups): the sum of R2 values for each microbial variable before and after batch effect correction for the balanced batch × treatment design. 

# precision & recall & F1 (ANOVA & sPLSDA)
## mean
acc_mean <- rbind(colMeans(precision_limma), colMeans(recall_limma), 
                  colMeans(F1_limma), c(colMeans(auc_splsda), sva = NA))
rownames(acc_mean) <- c('Precision', 'Recall', 'F1', 'AUC')
colnames(acc_mean) <- c('Before correction', 'Ground-truth data', 
                        'removeBatchEffect', 'ComBat', 
                        'PLSDA-batch', 'sPLSDA-batch', 'SVA')
acc_mean <- format(acc_mean, digits = 3)
knitr::kable(acc_mean, caption = 'Table 9: Simulation studies (three batch groups): summary of accuracy measurements before and after batch effect correction for the balanced batch × treatment design (mean).')
Table 4.5: Table 9: Simulation studies (three batch groups): summary of accuracy measurements before and after batch effect correction for the balanced batch × treatment design (mean).
Before correction Ground-truth data removeBatchEffect ComBat PLSDA-batch sPLSDA-batch SVA
Precision 0.986 0.954 0.949 0.940 0.957 0.856 0.964
Recall 0.667 0.891 0.902 0.903 0.896 0.884 0.934
F1 0.795 0.920 0.923 0.919 0.924 0.867 0.948
AUC 0.940 0.959 0.964 0.964 0.964 0.949 NA 
## sd
acc_sd <- rbind(apply(precision_limma, 2, sd), apply(recall_limma, 2, sd), 
                apply(F1_limma, 2, sd), c(apply(auc_splsda, 2, sd), NA))
rownames(acc_sd) <- c('Precision', 'Recall', 'F1', 'AUC')
colnames(acc_sd) <- c('Before correction', 'Ground-truth data', 
                      'removeBatchEffect', 'ComBat', 
                      'PLSDA-batch', 'sPLSDA-batch', 'SVA')
acc_sd <- format(acc_sd, digits = 1)
knitr::kable(acc_sd, caption = 'Table 10: Simulation studies (three batch groups): summary of accuracy measurements before and after batch effect correction for the balanced batch × treatment design (standard deviation).')
Table 4.6: Table 10: Simulation studies (three batch groups): summary of accuracy measurements before and after batch effect correction for the balanced batch × treatment design (standard deviation).
Before correction Ground-truth data removeBatchEffect ComBat PLSDA-batch sPLSDA-batch SVA
Precision 0.03 0.07 0.07 0.08 0.06 0.08 0.02
Recall 0.04 0.03 0.03 0.03 0.03 0.03 0.02
F1 0.03 0.04 0.04 0.04 0.03 0.04 0.01
AUC 0.02 0.02 0.02 0.02 0.02 0.02 NA

4.3.3 Unbalanced batch \(\times\) treatment design

The unbalanced design included 2, 10 and 2 samples from batch1, batch2 and batch3 respectively in trt1, 10, 2 and 10 samples from batch1, batch2 and batch3 in trt2.

Table 11: Unbalanced batch \(\times\) treatment design in the simulation study

Trt1 Trt2
Batch1 2 10
Batch2 10 2
Batch3 2 10 
nitr <- 50
N = 36
p_total = 300
p_trt_relevant = 100 
p_bat_relevant = 200 

# global variance (RDA)
gvar.before <- gvar.clean <- 
  gvar.rbe <- gvar.combat <- 
  gvar.wplsdab <- gvar.swplsdab <- 
  gvar.plsdab <- gvar.splsdab <- data.frame(treatment = NA, batch = NA,  
                                            intersection = NA, 
                                            residual = NA)

# individual variance (R2)
r2.trt.before <- r2.trt.clean <- 
  r2.trt.rbe  <- r2.trt.combat <- 
  r2.trt.wplsdab <- r2.trt.swplsdab <-
  r2.trt.plsdab <- r2.trt.splsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                       ncol = nitr))
r2.batch.before <- r2.batch.clean <- 
  r2.batch.rbe  <- r2.batch.combat <- 
  r2.batch.wplsdab <- r2.batch.swplsdab <-
  r2.batch.plsdab <- r2.batch.splsdab <- data.frame(matrix(NA, nrow = p_total, 
                                                           ncol = nitr))

# precision & recall & F1 (ANOVA)
precision_limma <- recall_limma <- F1_limma <- 
  data.frame(before = NA, clean = NA, 
             rbe = NA, combat = NA, 
             wplsda_batch = NA, swplsda_batch = NA, 
             sva = NA)

# auc (splsda)
auc_splsda <- 
  data.frame(before = NA, clean = NA, 
             rbe = NA, combat = NA, 
             wplsda_batch = NA, swplsda_batch = NA)


set.seed(70)
data.cor.res = corStruct(p = 300, zero_prob = 0.7)

for(i in 1: nitr){
  ### initial setup ###
  simulation <- simData_mnegbinom(batch.group = 3,
                                  mean.batch = 7, 
                                  sd.batch = 8, 
                                  mean.trt = 3, 
                                  sd.trt = 2, 
                                  mean.bg = 0, 
                                  sd.bg = 0.2, 
                                  N = 36, 
                                  p_total = 300, 
                                  p_trt_relevant = 100, 
                                  p_bat_relevant = 200, 
                                  percentage_overlap_samples = 1/6, 
                                  percentage_overlap_variables = 0.5, 
                                  data.cor = data.cor.res$data.cor, 
                                  disp = 10, prob_zero = 0, 
                                  seeds = i)
  
  set.seed(i)
  raw_count <- simulation$data
  raw_count_clean <- simulation$cleanData
  
  ## log transformation
  data_log <- log(raw_count + 1)
  data_log_clean <- log(raw_count_clean + 1)
  
  trt <- simulation$Y.trt
  batch <- simulation$Y.bat
  
  true.trt <- simulation$true.trt
  true.batch <- simulation$true.batch
  
  Batch_Trt.factors <- data.frame(Batch = batch, Treatment = trt)
  
  ### Original ###
  X <- data_log
  
  ### Clean data ###
  X.clean <- data_log_clean
  
  #####
  rownames(X) = rownames(X.clean) = names(trt) = names(batch) = 
    paste0('sample', 1:N)
  
  colnames(X) = colnames(X.clean) = paste0('otu', 1:p_total)
  
  ### Before correction ###
  # global variance (RDA)
  rda.before = varpart(scale(X), ~ Treatment, ~ Batch, 
                       data = Batch_Trt.factors)
  gvar.before[i,] <- rda.before$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.before <- lmFit(t(scale(X)), design = model.matrix(~ as.factor(trt)))
  fit.result.before <- topTable(eBayes(fit.before), coef = 2, number = p_total)
  otu.sig.before <- 
    rownames(fit.result.before)[fit.result.before$adj.P.Val <= 0.05]
  
  precision_limma.before <- 
    length(intersect(colnames(X)[true.trt], otu.sig.before))/
    length(otu.sig.before)
  recall_limma.before <- 
    length(intersect(colnames(X)[true.trt], otu.sig.before))/length(true.trt)
  F1_limma.before <- 
    (2*precision_limma.before*recall_limma.before)/
    (precision_limma.before + recall_limma.before)
  
  ## replace NA value with 0
  if(precision_limma.before == 'NaN'){
    precision_limma.before = 0
  }
  if(F1_limma.before == 'NaN'){
    F1_limma.before = 0
  }
  
  # individual variance (R2)
  indiv.trt.before <- c()
  indiv.batch.before <- c()
  for(c in seq_len(ncol(X))){
    fit.res1 <- lm(scale(X)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.before <- c(indiv.trt.before, fit.summary1$r.squared)
    indiv.batch.before <- c(indiv.batch.before, fit.summary2$r.squared)
  }
  r2.trt.before[ ,i] <-  indiv.trt.before
  r2.batch.before[ ,i] <-  indiv.batch.before
  
  
  # auc (sPLSDA)
  fit.before_plsda <- splsda(X = X, Y = trt, ncomp = 1)
  
  true.response <- rep(0, p_total)
  true.response[true.trt] = 1
  before.predictor <- as.numeric(abs(fit.before_plsda$loadings$X))
  roc.before_splsda <- roc(true.response, before.predictor, auc = TRUE)
  auc.before_splsda <- roc.before_splsda$auc
  
  
  ##############################################################################
  ### Ground-truth data ###
  # global variance (RDA)
  rda.clean = varpart(scale(X.clean), ~ Treatment, ~ Batch, 
                      data = Batch_Trt.factors)
  gvar.clean[i, ] <- rda.clean$part$indfract$Adj.R.squared
  
  
  # precision & recall & F1 (ANOVA)
  fit.clean <- lmFit(t(scale(X.clean)), design = model.matrix(~ as.factor(trt)))
  fit.result.clean <- topTable(eBayes(fit.clean), coef = 2, number = p_total)
  otu.sig.clean <- 
    rownames(fit.result.clean)[fit.result.clean$adj.P.Val <= 0.05]
  
  precision_limma.clean <- 
    length(intersect(colnames(X)[true.trt], otu.sig.clean))/
    length(otu.sig.clean)
  recall_limma.clean <- 
    length(intersect(colnames(X)[true.trt], otu.sig.clean))/length(true.trt)
  F1_limma.clean <- 
    (2*precision_limma.clean*recall_limma.clean)/
    (precision_limma.clean + recall_limma.clean)
  
  ## replace NA value with 0
  if(precision_limma.clean == 'NaN'){
    precision_limma.clean = 0
  }
  if(F1_limma.clean == 'NaN'){
    F1_limma.clean = 0
  }
  
  # individual variance (R2)
  indiv.trt.clean <- c()
  indiv.batch.clean <- c()
  for(c in seq_len(ncol(X.clean))){
    fit.res1 <- lm(scale(X.clean)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.clean)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.clean <- c(indiv.trt.clean, fit.summary1$r.squared)
    indiv.batch.clean <- c(indiv.batch.clean, fit.summary2$r.squared)
  }
  r2.trt.clean[ ,i] <-  indiv.trt.clean
  r2.batch.clean[ ,i] <-  indiv.batch.clean
  
  # auc (sPLSDA)
  fit.clean_plsda <- splsda(X = X.clean, Y = trt, ncomp = 1)
  
  clean.predictor <- as.numeric(abs(fit.clean_plsda$loadings$X))
  roc.clean_splsda <- roc(true.response, clean.predictor, auc = TRUE)
  auc.clean_splsda <- roc.clean_splsda$auc
  
  ##############################################################################
  ### removeBatchEffect corrected data ###
  X.rbe <-t(removeBatchEffect(t(X), batch = batch, 
                              design = model.matrix(~ as.factor(trt))))
  
  # global variance (RDA)
  rda.rbe = varpart(scale(X.rbe), ~ Treatment, ~ Batch, 
                    data = Batch_Trt.factors)
  gvar.rbe[i, ] <- rda.rbe$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.rbe <- lmFit(t(scale(X.rbe)), 
                   design = model.matrix( ~ as.factor(trt)))
  fit.result.rbe <- topTable(eBayes(fit.rbe), coef = 2, number = p_total)
  otu.sig.rbe <- rownames(fit.result.rbe)[fit.result.rbe$adj.P.Val <= 0.05]
  
  precision_limma.rbe <- length(intersect(colnames(X)[true.trt], otu.sig.rbe))/
    length(otu.sig.rbe)
  recall_limma.rbe <- length(intersect(colnames(X)[true.trt], otu.sig.rbe))/
    length(true.trt)
  F1_limma.rbe <- (2*precision_limma.rbe*recall_limma.rbe)/
    (precision_limma.rbe + recall_limma.rbe)
  
  ## replace NA value with 0
  if(precision_limma.rbe == 'NaN'){
    precision_limma.rbe = 0
  }
  if(F1_limma.rbe == 'NaN'){
    F1_limma.rbe = 0
  }
  
  # individual variance (R2)
  indiv.trt.rbe <- c()
  indiv.batch.rbe <- c()
  for(c in seq_len(ncol(X.rbe))){
    fit.res1 <- lm(scale(X.rbe)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.rbe)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.rbe <- c(indiv.trt.rbe, fit.summary1$r.squared)
    indiv.batch.rbe <- c(indiv.batch.rbe, fit.summary2$r.squared)
  }
  r2.trt.rbe[ ,i] <-  indiv.trt.rbe
  r2.batch.rbe[ ,i] <-  indiv.batch.rbe
  
  
  # auc (sPLSDA)
  fit.rbe_plsda <- splsda(X = X.rbe, Y = trt, ncomp = 1)
  
  rbe.predictor <- as.numeric(abs(fit.rbe_plsda$loadings$X))
  roc.rbe_splsda <- roc(true.response, rbe.predictor, auc = TRUE)
  auc.rbe_splsda <- roc.rbe_splsda$auc
  
  ##############################################################################
  ### ComBat corrected data ###
  X.combat <- t(ComBat(dat = t(X), batch = batch, 
                       mod = model.matrix( ~ as.factor(trt))))
  
  # global variance (RDA)
  rda.combat = varpart(scale(X.combat), ~ Treatment, ~ Batch, 
                       data = Batch_Trt.factors)
  gvar.combat[i, ] <- rda.combat$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.combat <- lmFit(t(scale(X.combat)), 
                      design = model.matrix( ~ as.factor(trt)))
  fit.result.combat <- topTable(eBayes(fit.combat), coef = 2, number = p_total)
  otu.sig.combat <- 
    rownames(fit.result.combat)[fit.result.combat$adj.P.Val <= 0.05]
  
  precision_limma.combat <- 
    length(intersect(colnames(X)[true.trt], otu.sig.combat))/
    length(otu.sig.combat)
  recall_limma.combat <- 
    length(intersect(colnames(X)[true.trt], otu.sig.combat))/
    length(true.trt)
  F1_limma.combat <- 
    (2*precision_limma.combat*recall_limma.combat)/
    (precision_limma.combat + recall_limma.combat)
  
  ## replace NA value with 0
  if(precision_limma.combat == 'NaN'){
    precision_limma.combat = 0
  }
  if(F1_limma.combat == 'NaN'){
    F1_limma.combat = 0
  }
  
  # individual variance (R2)
  indiv.trt.combat <- c()
  indiv.batch.combat <- c()
  for(c in seq_len(ncol(X.combat))){
    fit.res1 <- lm(scale(X.combat)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.combat)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.combat <- c(indiv.trt.combat, fit.summary1$r.squared)
    indiv.batch.combat <- c(indiv.batch.combat, fit.summary2$r.squared)
  }
  r2.trt.combat[ ,i] <-  indiv.trt.combat
  r2.batch.combat[ ,i] <-  indiv.batch.combat
  
  
  # auc (sPLSDA)
  fit.combat_plsda <- splsda(X = X.combat, Y = trt, ncomp = 1)
  
  combat.predictor <- as.numeric(abs(fit.combat_plsda$loadings$X))
  roc.combat_splsda <- roc(true.response, combat.predictor, auc = TRUE)
  auc.combat_splsda <- roc.combat_splsda$auc
  
  
  ##############################################################################
  ### wPLSDA-batch corrected data ###
  X.wplsda_batch.correct <- PLSDA_batch(X = X, 
                                        Y.trt = trt, Y.bat = batch, 
                                        ncomp.trt = 1, ncomp.bat = 2,
                                        balance = FALSE)
  X.wplsda_batch <- X.wplsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.wplsda_batch = varpart(scale(X.wplsda_batch), ~ Treatment, ~ Batch, 
                             data = Batch_Trt.factors)
  gvar.wplsdab[i, ] <- rda.wplsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.wplsda_batch <- lmFit(t(scale(X.wplsda_batch)), 
                            design = model.matrix( ~ as.factor(trt)))
  fit.result.wplsda_batch <- topTable(eBayes(fit.wplsda_batch), 
                                      coef = 2, number = p_total)
  otu.sig.wplsda_batch <- rownames(fit.result.wplsda_batch)[
    fit.result.wplsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.wplsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.wplsda_batch))/
    length(otu.sig.wplsda_batch)
  recall_limma.wplsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.wplsda_batch))/
    length(true.trt)
  F1_limma.wplsda_batch <- 
    (2*precision_limma.wplsda_batch*recall_limma.wplsda_batch)/
    (precision_limma.wplsda_batch + recall_limma.wplsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.wplsda_batch == 'NaN'){
    precision_limma.wplsda_batch = 0
  }
  if(F1_limma.wplsda_batch == 'NaN'){
    F1_limma.wplsda_batch = 0
  }
  
  # individual variance (R2)
  indiv.trt.wplsda_batch <- c()
  indiv.batch.wplsda_batch <- c()
  for(c in seq_len(ncol(X.wplsda_batch))){
    fit.res1 <- lm(scale(X.wplsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.wplsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.wplsda_batch <- c(indiv.trt.wplsda_batch, 
                                fit.summary1$r.squared)
    indiv.batch.wplsda_batch <- c(indiv.batch.wplsda_batch, 
                                  fit.summary2$r.squared)
  }
  r2.trt.wplsdab[ ,i] <-  indiv.trt.wplsda_batch
  r2.batch.wplsdab[ ,i] <-  indiv.batch.wplsda_batch
  
  # auc (sPLSDA)
  fit.wplsda_batch_plsda <- splsda(X = X.wplsda_batch, Y = trt, ncomp = 1)
  
  wplsda_batch.predictor <- as.numeric(abs(fit.wplsda_batch_plsda$loadings$X))
  roc.wplsda_batch_splsda <- roc(true.response, 
                                 wplsda_batch.predictor, auc = TRUE)
  auc.wplsda_batch_splsda <- roc.wplsda_batch_splsda$auc
  
  ##############################################################################
  ### sPLSDA-batch corrected data ###
  X.swplsda_batch.correct <- PLSDA_batch(X = X, 
                                         Y.trt = trt, 
                                         Y.bat = batch, 
                                         ncomp.trt = 1, 
                                         keepX.trt = length(true.trt), 
                                         ncomp.bat = 2,
                                         balance = FALSE)
  X.swplsda_batch <- X.swplsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.swplsda_batch = varpart(scale(X.swplsda_batch), ~ Treatment, ~ Batch, 
                              data = Batch_Trt.factors)
  gvar.swplsdab[i, ] <- rda.swplsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.swplsda_batch <- lmFit(t(scale(X.swplsda_batch)), 
                             design = model.matrix( ~ as.factor(trt)))
  fit.result.swplsda_batch <- topTable(eBayes(fit.swplsda_batch), coef = 2, 
                                       number = p_total)
  otu.sig.swplsda_batch <- rownames(fit.result.swplsda_batch)[
    fit.result.swplsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.swplsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.swplsda_batch))/
    length(otu.sig.swplsda_batch)
  recall_limma.swplsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.swplsda_batch))/
    length(true.trt)
  F1_limma.swplsda_batch <- 
    (2*precision_limma.swplsda_batch*recall_limma.swplsda_batch)/
    (precision_limma.swplsda_batch + recall_limma.swplsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.swplsda_batch == 'NaN'){
    precision_limma.swplsda_batch = 0
  }
  if(F1_limma.swplsda_batch == 'NaN'){
    F1_limma.swplsda_batch = 0
  }
  
  
  # individual variance (R2)
  indiv.trt.swplsda_batch <- c()
  indiv.batch.swplsda_batch <- c()
  for(c in seq_len(ncol(X.swplsda_batch))){
    fit.res1 <- lm(scale(X.swplsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.swplsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.swplsda_batch <- c(indiv.trt.swplsda_batch, 
                                 fit.summary1$r.squared)
    indiv.batch.swplsda_batch <- c(indiv.batch.swplsda_batch, 
                                   fit.summary2$r.squared)
  }
  r2.trt.swplsdab[ ,i] <-  indiv.trt.swplsda_batch
  r2.batch.swplsdab[ ,i] <-  indiv.batch.swplsda_batch
  
  # auc (sPLSDA)
  fit.swplsda_batch_plsda <- splsda(X = X.swplsda_batch, Y = trt, ncomp = 1)
  
  swplsda_batch.predictor <- as.numeric(abs(fit.swplsda_batch_plsda$loadings$X))
  roc.swplsda_batch_splsda <- roc(true.response, 
                                  swplsda_batch.predictor, auc = TRUE)
  auc.swplsda_batch_splsda <- roc.swplsda_batch_splsda$auc
  
  ##############################################################################
  ### PLSDA-batch corrected data ###
  X.plsda_batch.correct <- PLSDA_batch(X = X, 
                                       Y.trt = trt, Y.bat = batch, 
                                       ncomp.trt = 1, ncomp.bat = 2)
  X.plsda_batch <- X.plsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.plsda_batch = varpart(scale(X.plsda_batch), ~ Treatment, ~ Batch, 
                            data = Batch_Trt.factors)
  gvar.plsdab[i, ] <- rda.plsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.plsda_batch <- lmFit(t(scale(X.plsda_batch)), 
                           design = model.matrix( ~ as.factor(trt)))
  fit.result.plsda_batch <- topTable(eBayes(fit.plsda_batch), 
                                     coef = 2, number = p_total)
  otu.sig.plsda_batch <- rownames(fit.result.plsda_batch)[
    fit.result.plsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.plsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.plsda_batch))/
    length(otu.sig.plsda_batch)
  recall_limma.plsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.plsda_batch))/
    length(true.trt)
  F1_limma.plsda_batch <- 
    (2*precision_limma.plsda_batch*recall_limma.plsda_batch)/
    (precision_limma.plsda_batch + recall_limma.plsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.plsda_batch == 'NaN'){
    precision_limma.plsda_batch = 0
  }
  if(F1_limma.plsda_batch == 'NaN'){
    F1_limma.plsda_batch = 0
  }
  
  # individual variance (R2)
  indiv.trt.plsda_batch <- c()
  indiv.batch.plsda_batch <- c()
  for(c in seq_len(ncol(X.plsda_batch))){
    fit.res1 <- lm(scale(X.plsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.plsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.plsda_batch <- c(indiv.trt.plsda_batch, 
                               fit.summary1$r.squared)
    indiv.batch.plsda_batch <- c(indiv.batch.plsda_batch, 
                                 fit.summary2$r.squared)
  }
  r2.trt.plsdab[ ,i] <-  indiv.trt.plsda_batch
  r2.batch.plsdab[ ,i] <-  indiv.batch.plsda_batch
  
  # auc (sPLSDA)
  fit.plsda_batch_plsda <- splsda(X = X.plsda_batch, Y = trt, ncomp = 1)
  
  plsda_batch.predictor <- as.numeric(abs(fit.plsda_batch_plsda$loadings$X))
  roc.plsda_batch_splsda <- roc(true.response, 
                                plsda_batch.predictor, auc = TRUE)
  auc.plsda_batch_splsda <- roc.plsda_batch_splsda$auc
  
  ##############################################################################
  ### sPLSDA-batch corrected data ###
  X.splsda_batch.correct <- PLSDA_batch(X = X, 
                                        Y.trt = trt, 
                                        Y.bat = batch, 
                                        ncomp.trt = 1, 
                                        keepX.trt = length(true.trt), 
                                        ncomp.bat = 2)
  X.splsda_batch <- X.splsda_batch.correct$X.nobatch
  
  # global variance (RDA)
  rda.splsda_batch = varpart(scale(X.splsda_batch), ~ Treatment, ~ Batch, 
                             data = Batch_Trt.factors)
  gvar.splsdab[i, ] <- rda.splsda_batch$part$indfract$Adj.R.squared
  
  # precision & recall & F1 (ANOVA)
  fit.splsda_batch <- lmFit(t(scale(X.splsda_batch)), 
                            design = model.matrix( ~ as.factor(trt)))
  fit.result.splsda_batch <- topTable(eBayes(fit.splsda_batch), coef = 2, 
                                      number = p_total)
  otu.sig.splsda_batch <- rownames(fit.result.splsda_batch)[
    fit.result.splsda_batch$adj.P.Val <= 0.05]
  
  precision_limma.splsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.splsda_batch))/
    length(otu.sig.splsda_batch)
  recall_limma.splsda_batch <- 
    length(intersect(colnames(X)[true.trt], otu.sig.splsda_batch))/
    length(true.trt)
  F1_limma.splsda_batch <- 
    (2*precision_limma.splsda_batch*recall_limma.splsda_batch)/
    (precision_limma.splsda_batch + recall_limma.splsda_batch)
  
  ## replace NA value with 0
  if(precision_limma.splsda_batch == 'NaN'){
    precision_limma.splsda_batch = 0
  }
  if(F1_limma.splsda_batch == 'NaN'){
    F1_limma.splsda_batch = 0
  }
  
  
  # individual variance (R2)
  indiv.trt.splsda_batch <- c()
  indiv.batch.splsda_batch <- c()
  for(c in seq_len(ncol(X.splsda_batch))){
    fit.res1 <- lm(scale(X.splsda_batch)[ ,c] ~ trt)
    fit.summary1 <- summary(fit.res1)
    fit.res2 <- lm(scale(X.splsda_batch)[ ,c] ~ batch)
    fit.summary2 <- summary(fit.res2)
    indiv.trt.splsda_batch <- c(indiv.trt.splsda_batch, 
                                fit.summary1$r.squared)
    indiv.batch.splsda_batch <- c(indiv.batch.splsda_batch, 
                                  fit.summary2$r.squared)
  }
  r2.trt.splsdab[ ,i] <-  indiv.trt.splsda_batch
  r2.batch.splsdab[ ,i] <-  indiv.batch.splsda_batch
  
  # auc (sPLSDA)
  fit.splsda_batch_plsda <- splsda(X = X.splsda_batch, Y = trt, ncomp = 1)
  
  splsda_batch.predictor <- as.numeric(abs(fit.splsda_batch_plsda$loadings$X))
  roc.splsda_batch_splsda <- roc(true.response, 
                                 splsda_batch.predictor, auc = TRUE)
  auc.splsda_batch_splsda <- roc.splsda_batch_splsda$auc
  
  ##############################################################################
  ### SVA ###
  X.mod <- model.matrix(~ as.factor(trt))
  X.mod0 <- model.matrix(~ 1, data = as.factor(trt))
  X.sva.n <- num.sv(dat = t(X), mod = X.mod, method = 'leek')
  X.sva <- sva(t(X), X.mod, X.mod0, n.sv = X.sva.n)
  
  X.mod.batch <- cbind(X.mod, X.sva$sv)
  X.mod0.batch <- cbind(X.mod0, X.sva$sv)
  X.sva.p <- f.pvalue(t(X), X.mod.batch, X.mod0.batch)
  X.sva.p.adj <- p.adjust(X.sva.p, method = 'fdr')
  
  otu.sig.sva <- which(X.sva.p.adj <= 0.05)
  
  # precision & recall & F1 (ANOVA)
  precision_limma.sva <- 
    length(intersect(true.trt, otu.sig.sva))/length(otu.sig.sva)
  recall_limma.sva <- 
    length(intersect(true.trt, otu.sig.sva))/length(true.trt)
  F1_limma.sva <- 
    (2*precision_limma.sva*recall_limma.sva)/
    (precision_limma.sva + recall_limma.sva)
  
  ## replace NA value with 0
  if(precision_limma.sva == 'NaN'){
    precision_limma.sva = 0
  }
  if(F1_limma.sva == 'NaN'){
    F1_limma.sva = 0
  }
  
  
  # summary
  # precision & recall & F1 (ANOVA)
  precision_limma[i, ] <- c(`Before correction` = precision_limma.before, 
                            `Ground-truth data` = precision_limma.clean,
                            `removeBatchEffect` = precision_limma.rbe,
                            ComBat = precision_limma.combat,
                            `wPLSDA-batch` = precision_limma.wplsda_batch,
                            `swPLSDA-batch` = precision_limma.swplsda_batch,
                            SVA = precision_limma.sva)
  
  recall_limma[i, ] <- c(`Before correction` = recall_limma.before, 
                         `Ground-truth data` = recall_limma.clean,
                         `removeBatchEffect` = recall_limma.rbe,
                         ComBat = recall_limma.combat,
                         `wPLSDA-batch` = recall_limma.wplsda_batch,
                         `swPLSDA-batch` = recall_limma.swplsda_batch,
                         SVA = recall_limma.sva)
  
  F1_limma[i, ] <- c(`Before correction` = F1_limma.before, 
                     `Ground-truth data` = F1_limma.clean,
                     `removeBatchEffect` = F1_limma.rbe,
                     ComBat = F1_limma.combat,
                     `wPLSDA-batch` = F1_limma.wplsda_batch,
                     `swPLSDA-batch` = F1_limma.swplsda_batch,
                     SVA = F1_limma.sva)
  
  # auc (splsda)
  auc_splsda[i, ] <- c(`Before correction` = auc.before_splsda, 
                       `Ground-truth data` = auc.clean_splsda, 
                       `removeBatchEffect` = auc.rbe_splsda, 
                       ComBat = auc.combat_splsda, 
                       `wPLSDA-batch` = auc.wplsda_batch_splsda, 
                       `swPLSDA-batch` = auc.swplsda_batch_splsda)
  
  #  print(i)
  
}

4.3.4 Figures

# global variance (RDA)
prop.gvar.all <- rbind(`Before correction` = colMeans(gvar.before),
                       `Ground-truth data` = colMeans(gvar.clean),
                       removeBatchEffect = colMeans(gvar.rbe),
                       ComBat = colMeans(gvar.combat),
                       `wPLSDA-batch` = colMeans(gvar.wplsdab),
                       `swPLSDA-batch` = colMeans(gvar.swplsdab),
                       `PLSDA-batch` = colMeans(gvar.plsdab),
                       `sPLSDA-batch` = colMeans(gvar.splsdab))

prop.gvar.all[prop.gvar.all < 0] = 0
prop.gvar.all <- t(apply(prop.gvar.all, 1, function(x){x/sum(x)}))
colnames(prop.gvar.all) <- c('Treatment', 'Intersection', 'Batch', 'Residuals')

partVar_plot(prop.df = prop.gvar.all)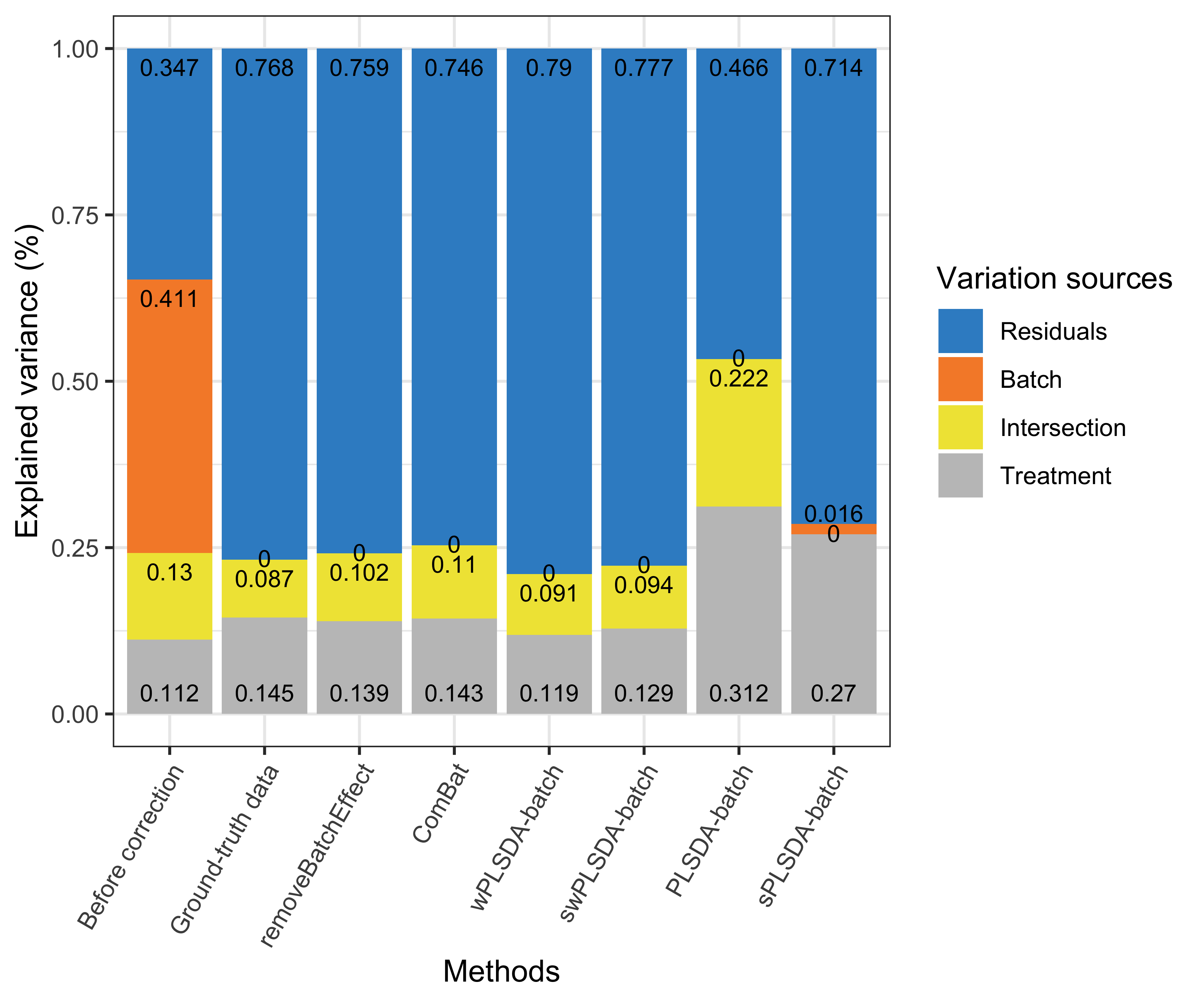
Figure 10: Simulation studies (three batch groups): comparison of explained variance before and after batch effect correction for the unbalanced batch × treatment design.

Figure 4.10: Figure 10: Simulation studies (three batch groups): comparison of explained variance before and after batch effect correction for the unbalanced batch × treatment design. 

################################################################################
# individual variance (R2)
## boxplot
# class
gclass <- c(rep('Treatment only', p_trt_relevant), 
            rep('Batch only', (p_total - p_trt_relevant)))
gclass[intersect(true.trt, true.batch)] = 'Treatment & batch'
gclass[setdiff(1:p_total, union(true.trt, true.batch))] = 'No effect'

gclass <- factor(gclass, levels = c('Treatment & batch', 
                                    'Treatment only', 
                                    'Batch only', 
                                    'No effect'))

before.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.before), 
                                      rowMeans(r2.batch.before)), 
                               type = as.factor(rep(c('Treatment','Batch'), 
                                                    each = 300)),
                               class = rep(gclass,2))
clean.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.clean), 
                                     rowMeans(r2.batch.clean)), 
                              type = as.factor(rep(c('Treatment','Batch'), 
                                                   each = 300)),
                              class = rep(gclass,2))
rbe.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.rbe), 
                                   rowMeans(r2.batch.rbe)), 
                            type = as.factor(rep(c('Treatment','Batch'), 
                                                 each = 300)),
                            class = rep(gclass,2))
combat.r2.df.ggp <- data.frame(r2 = c(rowMeans(r2.trt.combat), 
                                      rowMeans(r2.batch.combat)), 
                               type = as.factor(rep(c('Treatment','Batch'), 
                                                    each = 300)),
                               class = rep(gclass,2))
wplsda_batch.r2.df.ggp <- 
  data.frame(r2 = c(rowMeans(r2.trt.wplsdab), 
                    rowMeans(r2.batch.wplsdab)), 
             type = as.factor(rep(c('Treatment','Batch'), 
                                  each = 300)),
             class = rep(gclass,2))
swplsda_batch.r2.df.ggp <- 
  data.frame(r2 = c(rowMeans(r2.trt.swplsdab), 
                    rowMeans(r2.batch.swplsdab)), 
             type = as.factor(rep(c('Treatment','Batch'),
                                  each = 300)),
             class = rep(gclass,2))

all.r2.df.ggp <- rbind(before.r2.df.ggp, clean.r2.df.ggp,
                       rbe.r2.df.ggp, combat.r2.df.ggp,
                       wplsda_batch.r2.df.ggp, swplsda_batch.r2.df.ggp)

all.r2.df.ggp$methods <- rep(c('Before correction', 
                               'Ground-truth data', 
                               'removeBatchEffect', 
                               'ComBat',
                               'wPLSDA-batch', 
                               'swPLSDA-batch'), each = 600)

all.r2.df.ggp$methods <- factor(all.r2.df.ggp$methods, 
                                levels = unique(all.r2.df.ggp$methods))

ggplot(all.r2.df.ggp, aes(x = type, y = r2, fill = class)) +
  geom_boxplot(alpha = 0.80) +
  theme_bw() + 
  theme(text = element_text(size = 18),
        axis.title.x = element_blank(),
        axis.title.y = element_blank(),
        panel.grid.minor.x = element_blank(),
        panel.grid.major.x = element_blank(),
        legend.position = "right") + facet_grid(class ~ methods) + 
  scale_fill_manual(values=c('dark gray', color.mixo(4), 
                             color.mixo(5), color.mixo(9)))
Figure 11: Simulation studies (three batch groups): R2 values for each microbial variable before and after batch effect correction for the unbalanced batch × treatment design.

Figure 4.11: Figure 11: Simulation studies (three batch groups): R2 values for each microbial variable before and after batch effect correction for the unbalanced batch × treatment design. 

################################################################################
## barplot
# class
before.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.before), gclass, sum), 
                    tapply(rowMeans(r2.batch.before), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

clean.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.clean), gclass, sum), 
                    tapply(rowMeans(r2.batch.clean), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

rbe.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.rbe), gclass, sum), 
                    tapply(rowMeans(r2.batch.rbe), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

combat.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.combat), gclass, sum), 
                    tapply(rowMeans(r2.batch.combat), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

wplsda_batch.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.wplsdab), gclass, sum), 
                    tapply(rowMeans(r2.batch.wplsdab), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))

swplsda_batch.r2.df.bp <- 
  data.frame(r2 = c(tapply(rowMeans(r2.trt.swplsdab), gclass, sum), 
                    tapply(rowMeans(r2.batch.swplsdab), gclass, sum)), 
             type = as.factor(rep(c('Treatment','Batch'), each = 4)),
             class = factor(rep(levels(gclass),2), levels = levels(gclass)))


all.r2.df.bp <- rbind(before.r2.df.bp, clean.r2.df.bp,
                      rbe.r2.df.bp, combat.r2.df.bp,
                      wplsda_batch.r2.df.bp, swplsda_batch.r2.df.bp)


all.r2.df.bp$methods <- rep(c('Before correction', 
                              'Ground-truth data', 
                              'removeBatchEffect', 
                              'ComBat',
                              'wPLSDA-batch', 'swPLSDA-batch'), each = 8)

all.r2.df.bp$methods <- factor(all.r2.df.bp$methods, 
                               levels = unique(all.r2.df.bp$methods))

ggplot(all.r2.df.bp, aes(x = type, y = r2, fill = class)) +
  geom_bar(stat="identity") + 
  theme_bw() + 
  theme(text = element_text(size = 18),
        axis.title.x = element_blank(),
        axis.title.y = element_blank(),
        panel.grid.minor.x = element_blank(),
        panel.grid.major.x = element_blank(),
        legend.position = "right") + facet_grid(class ~ methods) + 
  scale_fill_manual(values=c('dark gray', color.mixo(4), 
                             color.mixo(5), color.mixo(9)))
Figure 12: Simulation studies (three batch groups): the sum of R2 values for each microbial variable before and after batch effect correction for the unbalanced batch × treatment design.

Figure 4.12: Figure 12: Simulation studies (three batch groups): the sum of R2 values for each microbial variable before and after batch effect correction for the unbalanced batch × treatment design. 

# precision & recall & F1 (ANOVA & sPLSDA)
## mean
acc_mean <- rbind(colMeans(precision_limma), colMeans(recall_limma), 
                  colMeans(F1_limma), c(colMeans(auc_splsda), sva = NA))
rownames(acc_mean) <- c('Precision', 'Recall', 'F1', 'AUC')
colnames(acc_mean) <- c('Before correction', 'Ground-truth data', 
                        'removeBatchEffect', 'ComBat', 
                        'wPLSDA-batch', 'swPLSDA-batch', 'SVA')
acc_mean <- format(acc_mean, digits = 3)
knitr::kable(acc_mean, caption = 'Table 12: Simulation studies (three batch groups): summary of accuracy measurements before and after batch effect correction for the unbalanced batch × treatment design (mean).')
Table 4.7: Table 12: Simulation studies (three batch groups): summary of accuracy measurements before and after batch effect correction for the unbalanced batch × treatment design (mean).
Before correction Ground-truth data removeBatchEffect ComBat wPLSDA-batch swPLSDA-batch SVA
Precision 0.637 0.972 0.862 0.834 0.915 0.863 0.648
Recall 0.811 0.884 0.897 0.904 0.855 0.844 0.872
F1 0.713 0.925 0.874 0.863 0.882 0.850 0.725
AUC 0.826 0.963 0.954 0.955 0.948 0.923 NA 
## sd
acc_sd <- rbind(apply(precision_limma, 2, sd), apply(recall_limma, 2, sd), 
                apply(F1_limma, 2, sd), c(apply(auc_splsda, 2, sd), NA))
rownames(acc_sd) <- c('Precision', 'Recall', 'F1', 'AUC')
colnames(acc_sd) <- c('Before correction', 'Ground-truth data', 
                      'removeBatchEffect', 'ComBat', 
                      'wPLSDA-batch', 'swPLSDA-batch', 'SVA')
acc_sd <- format(acc_sd, digits = 1)
knitr::kable(acc_sd, caption = 'Table 13: Simulation studies (three batch groups): summary of accuracy measurements before and after batch effect correction for the unbalanced batch × treatment design (standard deviation).')
Table 4.8: Table 13: Simulation studies (three batch groups): summary of accuracy measurements before and after batch effect correction for the unbalanced batch × treatment design (standard deviation).
Before correction Ground-truth data removeBatchEffect ComBat wPLSDA-batch swPLSDA-batch SVA
Precision 0.03 0.04 0.12 0.12 0.08 0.10 0.08
Recall 0.03 0.03 0.03 0.03 0.04 0.03 0.16
F1 0.03 0.03 0.07 0.07 0.04 0.06 0.11
AUC 0.02 0.02 0.02 0.02 0.02 0.02 NA

4.4 References

References

Hawinkel, Stijn, Federico Mattiello, Luc Bijnens, and Olivier Thas. 2019. “A Broken Promise: Microbiome Differential Abundance Methods Do Not Control the False Discovery Rate.” Briefings in Bioinformatics 20 (1): 210–21.
McGregor, Kevin, Aurélie Labbe, and Celia MT Greenwood. 2020. “MDiNE: A Model to Estimate Differential Co-Occurrence Networks in Microbiome Studies.” Bioinformatics 36 (6): 1840–47.
McMurdie, Paul J, and Susan Holmes. 2014. “Waste Not, Want Not: Why Rarefying Microbiome Data Is Inadmissible.” PLoS Computational Biology 10 (4): e1003531.
Quinn, Thomas P, Ionas Erb, Mark F Richardson, and Tamsyn M Crowley. 2018. “Understanding Sequencing Data as Compositions: An Outlook and Review.” Bioinformatics 34 (16): 2870–78.